dr Anna Barbaszewska-Wiśniowska

FUNKCJE WIELU ZMIENNYCH

Zad.1. Znajdź i naszkicuj dziedziny naturalne funkcji:

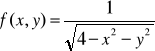
Zad.2. Naszkicuj mapy warstwicowe oraz zbadaj zachowanie funkcji na płaszczyznach układu współrzędnych

Zad.3. Wyznacz granice

;
;
;
;
;
;

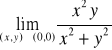
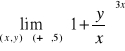
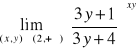
(wskazówka: sprawdź drogę do (0,0) po prostej y=x oraz po paraboli
)

Zad.4. Oblicz
,
dla funkcji

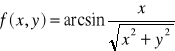
Zad.5. Oblicz
,

,
dla funkcji

Zad.6. Wykaż, że funkcja
spełnia równanie różniczkowe

Zad.7. Podaj wypowiedź i zilustruj twierdzenie Schwarza ( możesz wykorzystać przykłady z zadania 5).

Zad.8. Znajdź postać jawną i macierzową różniczki I i II rzędu
,

a.
,

b.
,

Zad.9. Oblicz

Zad.10. Znajdź kąt pomiędzy gradientami funkcji
w punktach
,

,

Zad.11. Podaj związki pomiędzy pochodnymi cząstkowymi, kierunkowymi, gradientem i różniczką dla funkcji różniczkowalnej

Zad.12. Oblicz pochodną kierunkową funkcji

a.
w punkcie
w kierunku tworzącym z osią Ox kąt

b.
w punkcie
w kierunku wektora

c.
w punkcie
w kierunku do punktu

Zad.13. Podaj pełną wypowiedź twierdzeń o ekstremach funkcji wielu zmiennych oraz opisz sposób korzystania z nich. Wyznacz ekstrema funkcji.

Zad.14. Znajdź płaszczyzny styczne
i proste normalne
kolejno do powierzchni
danych równaniami
,
odpowiednio w punktach
i

---