Przestrzeń probabilistyczna
W rachunku prawdopodobieństwa pojęcie zdarzenia elementarnego jest pojęciem pierwotnym. Pojedyncze zdarzenia elementarne oznaczać będziemy: ω1, ω2, ω3, …, a zbiór (przestrzeń) zdarzeń elementarnych: Ω.
Rozważmy rodzinę S podzbiorów przestrzeni zdarzeń elementarnych, która spełnia następujące warunki:
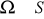
;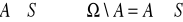
;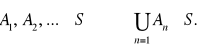
Rodzinę S spełniającą własności 1 - 3 nazywamy σ-ciałem lub σ-algebrą zbiorów.
Każdy zbiór należący do rodziny S nazywamy zdarzeniem losowym.
Uwaga 1.
Jeżeli zbiór zdarzeń elementarnych jest skończony, to w dalszym ciągu będziemy przyjmować, że S jest rodziną wszystkich podzbiorów zbioru zdarzeń elementarnych Ω.
Ponieważ zdarzenia losowe są zbiorami, więc działania na zdarzeniach będziemy oznaczać takimi samymi symbolami jak działania na zbiorach.
Pewne szczególne zdarzenia losowe mają swoje nazwy:
Ω - zdarzenie pewne,
Ø (zbiór pusty) - zdarzenie niemożliwe,
![]()
- zdarzenie przeciwne do zdarzenia A.
Jeżeli ponadto dla dwóch zdarzeń A i B mamy:
![]()
, to mówimy, że zdarzenie A pociąga za sobą zdarzenie B;
![]()
= Ø, to mówimy, ze zdarzenia A i B są rozłączne (wykluczają się).
Definicja prawdopodobieństwa
W zbiorze zdarzeń losowych wprowadzimy funkcję prawdopodobieństwa w następujący sposób (A. Kołmogorow, 1933).
Prawdopodobieństwem nazywamy funkcję P: S →R (przyporządkowującą każdemu zdarzeniu losowemu A liczbę P(A) nazywaną prawdopodobieństwem zajścia zdarzenia A) taką, że spełnione są następujące warunki:
W1 P(A) ≥ 0 dla każdego zdarzenia ![]()
;
W2 P(Ω)=1,
W3 Jeżeli A1, A2 , A3, …tworzą ciąg zdarzeń losowych parami rozłącznych
(tzn. dla i ≠ j ![]()
mamy: Ai![]()
Aj=Ø), to
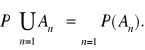
Każdą funkcję spełniającą warunki W1 - W3 nazywa się miarą probabilistyczną.
Trójkę uporządkowaną (Ω, S, P), gdzie Ω jest przestrzenią zdarzeń elementarnych, S - przestrzenią zdarzeń losowych, a P - prawdopodobieństwem, nazywamy przestrzenią probabilistyczną.
Z definicji prawdopodobieństwa wynikają następujące własności:
W1. P(Ø) = 0;
W2. Dla A∈S: P(A)≤1;
W3. Jeśli A∈S, to P(A′) = 1 - P(A);
W4. Jeśli A, B są zdarzeniami i A⊂B, to P(A) ≤ P(B);
W5. Jeśli A∩B=Ø, to P(A∪B) = P(A) + P(B);
W6. Jeśli A,B∈S, to P(A∪B) = P(A) + P(B) - P(A∩B).
Uwaga 2.
W szczególnym przypadku, jeśli:
zbiór zdarzeń elementarnych jest skończony: Ω = { ω1, ω2, … , ωn },
wszystkie zdarzenia elementarne są jednakowo prawdopodobne, czyli:
P({ω1}) = P({ω2}) = … = P({ωn}) =![]()
,
to prawdopodobieństwo zajścia dowolnego zdarzenia A = { ωi1, ωi2, … , ωik} składającego się
z k zdarzeń elementarnych, dane jest wzorem:
![]()
Powyższy wzór określa tzw. definicję klasyczną prawdopodobieństwa (definicję Laplace'a).
Podamy teraz przykład podkreślając fakt, ze mając dany eksperyment losowy musimy najpierw określić przestrzeń probabilistyczną, aby obliczyć prawdopodobieństwa interesujących nas zdarzeń losowych.
Przykład 1.
Rzucamy dwiema różnokolorowymi symetrycznymi sześciennymi kostkami do gry
i notujemy liczbę oczek wyrzuconych na poszczególnych kostkach.
Wtedy zbiór zdarzeń elementarnych możemy krótko zapisać następująco:
Ω = {(i,j): i,j∈{1,2,3,4,5,6}}
lub w pełnej formie:
Ω={(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}.
Zbiór zdarzeń elementarnych jest skończony i ma 36 elementów (tyle ile jest dwuelementowych wariacji z powtórzeniami ze zbioru 6-cio elementowego: ![]()
= 62).
Jako rodzinę zdarzeń losowych S przyjmujemy wszystkie podzbiory zbioru zdarzeń elementarnych.
Wykorzystując definicję klasyczną, obliczymy prawdopodobieństwa następujących zdarzeń losowych.
A - zdarzenie polegające na tym, że suma wyrzuconych oczek na obydwu kostkach nie przekracza 4.
Zdarzeniu A sprzyja 6 zdarzeń elementarnych: (1,1), (1,2), (1,3), (2,1), (2,2), (3,1), więc ![]()
.
b) B - zdarzenie polegające na tym, że iloczyn wyrzuconych oczek wynosi co najmniej 20.
Zauważmy, że zdarzeniu B sprzyjają następujące zdarzenia elementarne: (4,5), (4,6), (5,4), (5,5), (5,6), (6,4), (6,5), (6,6).
Tak więc P(B) = ![]()
c) C - zdarzenie polegające na tym, że moduł różnicy wyrzuconych oczek wynosi 2.
Zdarzeniu C sprzyjają zdarzenia elementarne: (1,3), (3,1), (2,4), (4,2), (3,5), (5,3), (4,6), (6,4), tak więc: P(C) = ![]()
Przyjmijmy teraz, że eksperyment jest tak określony, że rzut uznaje się za nieważny i powtarzamy go, jeśli na jednej z kostek wypadnie liczba oczek mniejsza niż 3.
Wtedy przestrzeń zdarzeń elementarnych jest następująca:
Ω1 = {(3,3), (3,4), (3,5), (3,6),
(4,3), (4,4), (4,5), (4,6),
(5,3), (5,4), (5,5), (5,6),
(6,3), (6,4), (6,5), (6,6)}.
Jeśli zdarzenia A, B, C określimy słownie tak samo jak wyżej, to z uwagi na to, że przestrzeń probabilistyczna jest inna, mamy prawdopodobieństwa tych zdarzeń:
P(A) = P(Ø) = 0.
P(B) =
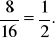
P(C) =
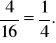
Prawdopodobieństwo warunkowe
Niech (Ω,S,P) będzie przestrzenią probabilistyczną, zaś ![]()
dowolnym ustalonym zdarzeniem o dodatnim prawdopodobieństwie. Prawdopodobieństwem warunkowym zajścia zdarzenia ![]()
pod warunkiem zajścia zdarzenia B nazywamy liczbę P(A/B) określoną wzorem:
P(A/B) = ![]()
Z definicji tej wynika użyteczny wzór:
P(A![]()
B) = P(A/B)⋅ P(B),
który można uogólnić na większą liczbę zdarzeń:
![]()
i ogólnie dla n zdarzeń losowych:
![]()
Przykład 2.
Producent zapewnia, że prawdopodobieństwo awarii automatu wytwarzającego pewien detal wynosi 5% w pierwszym roku eksploatacji. Jeśli w pierwszym roku automat nie ulegnie awarii, to prawdopodobieństwo awarii w drugim roku użytkowania wyniesie 10%. Jeśli automat będzie sprawny przez dwa lata, to z prawdopodobieństwem 20% ulegnie awarii w trzecim roku użytkowania. Jakie jest prawdopodobieństwo, że automat nie ulegnie awarii w czasie trzech pierwszych lat użytkowania?
Niech Ai oznacza zdarzenie, że automat nie ulegnie awarii w i-tym roku użytkowania, i = 1,2,3. Wtedy mamy: P(A1) = 0,95, P(A2/A1)=0,90, P(A3/(A1∩A2))=0,80.
Wykorzystując podaną równość otrzymamy:
P(A1∩A2∩A3) = P(A1) ⋅P(A2/A1)⋅P(A3/(A1∩A2)) = 0,95⋅0,90⋅0,80 = 0,684.
Prawdopodobieństwo tego, że automat nie ulegnie awarii w czasie trzech pierwszych lat eksploatacji wynosi 0,684.
Prawdopodobieństwo całkowite i twierdzenie Bayesa
Zdarzenia ![]()
tworzą zupełny układ zdarzeń w przestrzeni probabilistycznej (Ω, S, P), jeżeli spełniają warunki:
1. ![]()
2. Ai![]()
Aj = Ø dla i≠j (zdarzenia są parami rozłączne);
3. P(Ai) > 0, i = 1, 2, … ,n.
Twierdzenie 1. (wzór na prawdopodobieństwo całkowite)
Jeżeli zdarzenia A1, A2, … ,An ![]()
S tworzą zupełny układ zdarzeń w przestrzeni probabilistycznej (Ω, S, P), to dla dowolnego zdarzenia B![]()
S zachodzi równość:
![]()
Twierdzenie 2. (Bayesa)
Jeżeli zdarzenia A1, A2, … ,An ![]()
S tworzą zupełny układ zdarzeń w przestrzeni probabilistycznej (Ω, S, P), to dla każdego zdarzenia B o prawdopodobieństwie dodatnim zachodzi równość:
![]()
Uwaga 3.
Prawdopodobieństwa P(Ak/B) nazywamy prawdopodobieństwami a posteriori, gdyż określa ono szansę zajścia zdarzenia Ak dopiero po zajściu zdarzenia B, natomiast P(Ak) nazywamy prawdopodobieństwami a priori.
Przykład 3.
Przed egzaminem z matematyki podane zostały pytania egzaminacyjne dopuszczające do egzaminu pisemnego:
40 pytań z algebry, 60 pytań z geometrii i 100 pytań z analizy. Student przed egzaminem zna odpowiedź na 35 pytań z algebry, 50 pytań z geometrii i 80 pytań z analizy. Student jest dopuszczony do zdawania egzaminu, jeżeli odpowie dobrze na jedno wylosowane pytanie.
Jakie jest prawdopodobieństwo tego, że student zostanie dopuszczony do egzaminu?
Student został dopuszczony do egzaminu, jakie jest prawdopodobieństwo, że wylosował pytanie z analizy?
Przyjmijmy oznaczenia:
A1 - zdarzenie polegające na tym, że student wylosuje pytanie z algebry,
A2 - zdarzenie polegające na tym, że student wylosuje pytanie z geometrii,
A3 - zdarzenie polegające na tym, że student wylosuje pytanie z analizy,
B - student został dopuszczony do egzaminu pisemnego.
Przy tych oznaczeniach oczywiste jest, że zdarzenia A1, A2, A3 tworzą zupełny układ zdarzeń a prawdopodobieństwa a priori są równe:
![]()
, ![]()
, ![]()
.
Znane są także prawdopodobieństwa warunkowe:
![]()
, ![]()
, ![]()
.
Aby wyznaczyć prawdopodobieństwo tego, że student zostanie dopuszczony do egzaminu należy skorzystać ze wzoru na prawdopodobieństwo całkowite:

Aby wyznaczyć prawdopodobieństwo tego, że student wylosował pytanie z analizy, jeżeli został dopuszczony do egzaminu, należy skorzystać ze wzoru Bayesa:
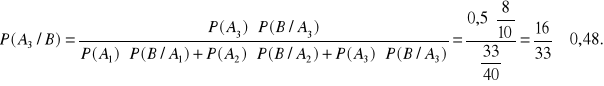
Niezależność zdarzeń
Ważnym pojęciem teorii prawdopodobieństwa jest niezależność zdarzeń losowych. Intuicyjnie oznacza to, że zdarzenie A nie zależy od zdarzenia B, jeżeli informacja, że zaszło zdarzenie B nie ma wpływu na prawdopodobieństwo zajścia zdarzenia A i odwrotnie. To intuicyjne podejście prowadzi więc do dwóch warunków:
P(A/B) = P(A) i P(B/A) = P(B)
Z definicji prawdopodobieństwa warunkowego i z powyższych równości wynika, że niezależność zdarzeń można określić następująco w ustalonej przestrzeni probabilistycznej.
Zdarzenia A i B są niezależne jeżeli: P(A![]()
B) = P(A)P(B).
Uwaga 4.
Wnioskiem wynikającym wprost z tej definicji jest fakt: jeśli dwa zdarzenia A i B
o niezerowych prawdopodobieństwach są niezależne, to zdarzenia te nie mogą być rozłączne.
W przypadku większej liczby zdarzeń niezależność definiujemy następująco:
Mówimy, że w ustalonej przestrzeni probabilistycznej zdarzenia A1, A2, A3, … , An są niezależne (wzajemnie niezależne, zespołowo niezależne) jeżeli dla każdego naturalnego k ≤ n oraz dla każdego ciągu indeksów 1≤i1< i2 < … < ik ≤ n zachodzi równość:
![]()
Przykład 4.
Rozważmy przestrzeń probabilistyczną z przykładu 1. związaną z rzutem dwiema symetrycznymi kostkami sześciennymi do gry.
Rozważmy zdarzenia:
A - na drugiej kostce wypadnie „szóstka”,
B - na pierwszej kostce wypadnie nieparzysta liczba oczek,
C - na obu kostkach wypadnie liczba oczek, których suma jest parzysta.
Wtedy:
A = {(1,6), (2,6), (3,6), (4,6), (5,6), (6,6)},
B = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)},
C = {(1,1), (1,3), (1,5), (2,2), (2,4), (2,6), (3.1), (3,3), (3,5),
(4,2), (4,4), (4,6), (5.1), (5,3), (5,5), (6,2), (6,4), (6,6)}.
Prawdopodobieństwa tych zdarzeń wynoszą:
![]()
, ![]()
, ![]()
.
Wyznaczamy teraz iloczyny zdarzeń i ich prawdopodobieństwa:
A∩B = {(1,6), (3,6), (6,6)}, ![]()
,
A∩C = {(2,6), (4,6), (6,6)}, ![]()
,
B∩C = {(1,1), (1,3), (1,5), (3.1), (3,3), (3,5), (5.1), (5,3), (5,5)}. ![]()
,
A∩B∩C = ∅, ![]()
.
Mamy więc następujące równości:
![]()
![]()
![]()
z których wynika, że zdarzenia dane są parami niezależne.
Nie są one jednak niezależne (zespołowo niezależne), bo:
![]()
ZADANIE
Na przenośnik taśmowy trafiają detale produkowane przez trzy automaty. Pierwszy automat wytwarza 6% braków, drugi - 5% a trzeci - 4% braków. Wielkość produkcji tych automatów ma się tak, jak 2:4:5. Wybrano losowo z przenośnika detal, który okazał się brakiem. Jakie jest prawdopodobieństwo tego, że wyprodukował go pierwszy automat?
ZADANIA DOMOWE
Na przenośnik taśmowy trafiają detale produkowane przez trzy automaty. Pierwszy automat wytwarza 6% braków, drugi - 5% a trzeci - 4% braków. Wielkość produkcji tych automatów ma się tak, jak 2:4:5. Wybrano losowo z przenośnika detal, który okazał się brakiem. Jakie jest prawdopodobieństwo tego, że wyprodukował go pierwszy automat?
Fabryka sprowadza pewne detale od trzech producentów. Wadliwość produkcji pierwszego dostawcy wynosi 5%, drugiego - 4%, a trzeciego - 2%. Dostawcy ci pokrywają zapotrzebowanie fabryki odpowiednio w 25%, 30% i 45%.
Obliczyć prawdopodobieństwo tego, że losowo wybrany detal jest wadliwy.
Obliczyć prawdopodobieństwo tego, że losowo wybrany detal, który okazał się wadliwy, został wyprodukowany przez trzeciego dostawcę.
70% mężczyzn i 15% kobiet ogląda mecze piłki nożnej w telewizji. Z grupy 200 kobiet i 300 mężczyzn wybrano losowo jedną osobę.
Jakie jest prawdopodobieństwo, że wybrana osoba ogląda mecze piłki nożnej w telewizji?
Wylosowano osobę i okazało się, że ogląda ona mecze w telewizji. Jakie jest prawdopodobieństwo, że jest to kobieta?
Wyszukiwarka
Podobne podstrony:
odpowiedzi 2007, WSEIZ, Budownictwo, Semestr III, 3. Materiały do izolacji cieplnej
belka MB, WSEIZ, Budownictwo, Semestr III, 8. Wytrzymałość materiałów, Wykład
sprawozdanie 3, WSEIZ, Budownictwo, Semestr III, 8. Wytrzymałość materiałów, Laborki
ROZWIĄZYWANIE BELEK, WSEIZ, Budownictwo, Semestr III, 8. Wytrzymałość materiałów, Wykład
Wahadło matematyczne i fizyczne-teoria, WSEIZ, Budownictwo, Semestr III, 1. Fizyka, Laborki
Przyklad 3 MB Kratownica, WSEIZ, Budownictwo, Semestr III, 8. Wytrzymałość materiałów, Wykład
Przyklad 5 MB Kratownica, WSEIZ, Budownictwo, Semestr III, 8. Wytrzymałość materiałów, Wykład
Schody 1, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budownictwo Ogólne,
Materialy budowlane pytania 2008, PG Budownictwo, Semestr III, Materiały budowlane, egzaminy itp, In
4a, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Technologia Betonu, betony
POLITECHNIKA BIAŁOSTOCKA, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budo
cw7, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Technologia Betonu, beton
cw-9 p, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Wytrzymałośc Materiałó
Mur1, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budownictwo Ogólne, kolo
betony zaliczenie, Budownictwo semestr III, betony
więcej podobnych podstron