Dominika Kobiałka

L 4

Cwiczenie nr 21

Rozładowanie kondensatora

Zagadnienia do samodzielnego opracowania:

1. Pojemność elektryczna - definicja, rodzaje kondensatorów.

2. Rozładowanie i ładowanie kondensatora, równanie krzywej ładowania i rozładowania, stała czasowa obwodu.

3. Wyznaczenie pojemności kondensatora na podstawie jego krzywej rozładowania.

4. Wyznaczenie wartości ładunku zgromadzonego na okładkach kondensatora na podstawie krzywej rozładowania.

Wykonanie ćwiczenia:

1. Połączyć układ wg. schematu. Odczytać wartość oporu z opornicy dekadowej.

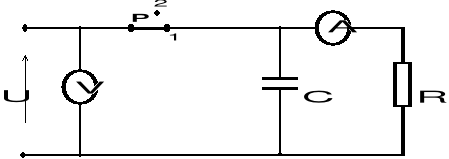
2. Naładować kondensator, gdy wartość prądu ustali się przyjąć ją jako I0 dla chwili t = 0 (s).

3. Przełączyć przełącznik P i jednocześnie włączyć sekundomierz. Przeprowadzić pomiary natężenia prądu rozładowania kondensatora I = f(t).

4. Sporządzić wykres prądu rozładowania : I = f(t) oraz wykres
.

5. Wartość ładunku zgromadzonego na okładkach kondensatora można obliczyć wyznaczając wartość pola powierzchni zawartego pomiędzy osiami współrzędnych a wykresem I = f(t).

6. Wyznaczyć pojemność kondensatora :

gdzie : Q - wartość ładunku zgromadzonego na okładkach kondensatora,

U - napięcie między okładkami, które w tym przypadku jest równe napięciu zasilającemu obwód pomiarowy.

7. Obliczyć stałą czasową obwodu korzystając z wykresu

U	R	I0	t	I	Q	C
[ V ]	[ kΩ ]	[ mA ]	[ s ]	[ mA ]	[ μC ]	[ μF ]	[ s ]
6	40	150	0 1,79 3,12 4,8 5,61 8,66 10,48 13,3 15,78 19,2 22,78 27,83 33,25 42,82 58,98	150 140 130 120 110 100 90 80 70 60 50 40 30 20 10	2978	496,33	19,8532

Ładunek zgromadzony na okładkach kondensatora wyznaczamy licząc pole powierzchni pod krzywą I = f(t) ( patrz rys. 1 ) jako sumę pól trapezów wyznaczonych przez punkty pomiarowe. Możemy tak postąpić ponieważ zaproksymowana krzywa zawiera te punkty i błąd jaki popełniamy jest niewielki.

Ładunek zgromadzony na okładkach kondensatora obliczamy jako sumę pól trapezów :

gdzie i = 1,2,..15 ( punkty pomiarowe ), więc całkowity ładunek obliczamy jako :

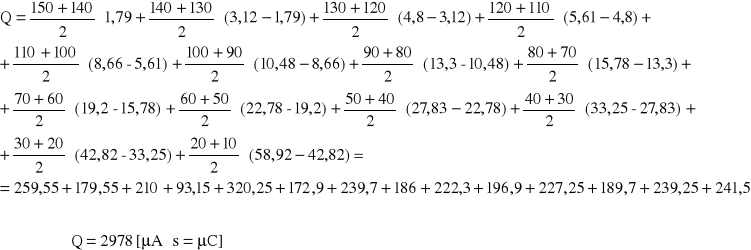
Pojemność badanego kondensatora wynosi :

Stała czasowa obwodu = R C jest równa wartości bezwzględnej z odwrotności współczynnika nachylenia prostej
(rys. 2 ).

a - współczynnik nachylenia prostej obliczony metodą najmniejszych kwadratów

Możemy ją także obliczyć znając rezystancję R i pojemność C

Błędy mierników :

bezwzględny :

względny procentowy :

gdzie k - klasa dokładności miernika

ZP - zakres pomiarowy miernika

XM - wartość mierzona

Błąd pomiaru napięcia

Błąd pomiaru prądu :

Błąd bezwzględny pomiaru czasu określamy jako czas reakcji wykonującego pomiar

błąd względny :

Wnioski:

Pojemność badanego kondensatora C = 496,33 F, stała czasowa = 19,85 s.

Wyznaczanie pojemności w sposób przedstawiony w ćwiczeniu jest dość kłopotliwe, gdyż czasochłonne jest obliczanie ładunku zgromadzonego w kondensatorze jako pola pod krzywą rozładowania I = f(t). Jak widać na rys. 1 w obwodzie rozładowania kondensatora prąd maleje asymptotycznie do 0. Teoretycznie prąd nigdy nie osiągnie wartości 0 ( w nieskończoności ), w praktyce nastąpi to po kilku stałych czasowych.

---