Robert Maniura

Sprawozdanie z ćwiczenia nr B-13: Napięcie powierzchniowe.

1. Wstęp teoretyczny:

Cząsteczka we wnętrzu fazy ciekłej znajduje się w polu potencjalnym, którego energia ma symetrię kulistą, Cząsteczka leżąca na granicy fazy podlega oddziaływaniu niesymetrycznemu; w skrajnym przypadku, gdy po drugiej stronie granicy znajduje się próżnia lub gaz rozrzedzony, podlega oddziaływaniu tylko od strony fazy skondensowanej.

Nie inaczej ma się rzecz w przypadku wnętrza i powierzchni fazy stałej. Wprawdzie energia oddziaływania cząsteczki z jej najbliższymi sąsiadami nie wykazuje symetrii kulistej, lecz taką, jaka wynika ze struktury kryształu i geometrii cząsteczki, jednakże i tu oddziaływania międzycząsteczkowe we wnętrzu fazy wzajemnie się kompensują, podczas gdy w pobliżu granicy faz kompensacja taka nie zachodzi.

Ponieważ w fazach skondensowanych dominują oddziaływania o ujemnej energii potencjalnej (przyciąganie międzycząsteczkowe), cząsteczki znajdujące się na granicy oddzielającej fazę skondensowaną od próżni lub gazu rozrzedzonego są niejako „wciągane” do wnętrza fazy skondensowanej.

Oznacza to, że powiększanie swobodnej powierzchni fazy skondensowanej, tj. przeniesienie na nią pewnej liczby cząsteczek z wnętrza fazy, wymaga wykonania określonej pracy. Jeżeli operację tę wykonamy w stałej temperaturze, nie zmieniając objętości fazy skondensowanej i w sposób quasi - statyczny, to praca ta równa będzie zmianie energii swobodnej układu. Mówiąc językiem termodynamiki, ta część układu, która znajduje się w bezpośrednim sąsiedztwie granicy faz, wykazuje pewien nadmiar energii swobodnej w stosunku do takiej samej masy układu, wziętej z jego wnętrza. Nadmiar ten nie zależy przy tym od masy rozpatrywanej części układu, lecz jedynie od wielkości powierzchni, będąc do niej wprost proporcjonalny. Stąd też pochodna energii swobodnej względem wielkości powierzchni fazy skondensowanej będzie miarą właściwej powierzchniowej energii swobodnej tej fazy. Wielkość tę oznaczamy symbolem σ:

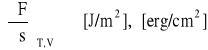
i nazywamy zazwyczaj napięciem powierzchniowym fazy.

Rozważania powyższe można uogólnić na przypadek granicy między dowolnymi dwiema fazami, 1 i 2. Mówimy wówczas o właściwej energii swobodnej granicy faz
lub o napięciu międzyfazowym:

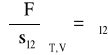
Podobnie jak wprowadziliśmy właściwą energię swobodną granicy faz, możemy zdefiniować i pozostałe funkcje termodynamiczne: właściwą energię wewnętrzną granicy faz (powierzchni):

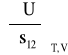
oraz właściwą entropię granicy faz (powierzchni):

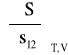
Korzystając z ogólnej zależności:

znajdziemy między nimi związek:

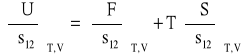
i korzystając z relacji:

zapisać można w postaci:

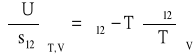
Pamiętając, że σ₁₂ określa pracę wykonaną przy zwiększaniu powierzchni granicy faz o jednostkę, możemy równanie ostatnie traktować jako zapis pierwszej zasady termodynamiki dla jednostkowej powierzchni „fazy powierzchniowej”:

Porównując ostatnie wyrażenie z wzorem przedostatnim widzimy, że wyraz
przedstawia ciepło wymienione przez układ podczas zwiększania powierzchni granicy faz o jednostkę w warunkach izochoryczno - izotermicznych. Ponieważ zazwyczaj napięcie międzyfazowe maleje ze wzrostem temperatury (w szczególności odnosi się to do napięcia powierzchniowego), zwiększeniu powierzchni granicy faz o s₁₂ towarzyszy nie tylko wykonanie pracy σ₁₂s₁₂, lecz również pochłonięcie ciepła
. Widzimy również, że zwiększenie powierzchni powoduje z reguły przyrost entropii układu.

Przedstawiony wyżej opis termodynamiczny odnosi się ogólnie do każdej granicy faz: między dwoma ciałami stałymi, między ciałem stałym a cieczą , między ciałem stałym a gazem, między dwoma cieczami, wreszcie między cieczą a gazem; lecz tylko w dwóch ostatnich przypadkach objęte tym opisem własności granicy faz są łatwo dostrzegalne, a wielkość właściwej powierzchniowej energii swobodnej jest bezpośrednio mierzalna.

2. Opracowanie wyników:

Obliczam napięcie powierzchniowe roztworów i substancji czystych względem substancji wzorcowej - wody. Napięcie powierzchniowe obliczam posługując się zależnością:

gdzie: s_x - napięcie powierzchniowe badanej substancji (cykloheksanu lub 1,4-dioksanu) lub roztworów; s_w - napięcie powierzchniowe wody równe 72,75*10^-3 [J/m²]; h - różnica odczytu na manometrze dla poszczególnych roztworów (substancji) przy otwartym i zamkniętym kranie trójdrożnym do atmosfery.

Wyznaczam liczbę moli oraz ułamki molowe dla poszczególnych roztworów:

gdzie: n - liczba moli; d - gęstość substancji; V - objętość substancji dodana do odpowiedniego roztworu; M - masa molowa substancji; (x = cykloheksan (c) lub 1,4-dioksym (d)).

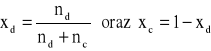
L.p.	Różnica odczytu na manometrze [cm]	Objętość cykloheksanu [m3]	Objętość 1,4-dioksanu [m3]	Liczba moli cykloheksanu [mol]	Liczba moli 1,4-dioksanu [mol]	Ułamek molowy cykloheksanu	Ułamek molowy 1,4-dioksanu	Napięcie powierzch-niowe roztworów [J/m2]
1	5,1	10,0*10^-6	0	0,0919	0,0000	1,0000	0,0000	0,0267
2	5,1	9,62*10^-6	0,38*10^-6	0,0884	0,0044	0,9521	0,0479	0,0267
3	5,2	9,23*10^-6	0,77*10^-6	0,0848	0,0090	0,9041	0,0959	0,0272
4	5,3	8,42*10^-6	1,58*10^-6	0,0774	0,0185	0,8072	0,1928	0,0277
5	5,3	7,56*10^-6	2,44*10^-6	0,0695	0,0285	0,7095	0,2905	0,0277
6	5,4	6,66*10^-6	3,34*10^-6	0,0612	0,0390	0,6110	0,3890	0,0283
7	5,5	5,71*10^-6	4,29*10^-6	0,0525	0,0501	0,5115	0,4885	0,0288
8	5,6	4,70*10^-6	5,30*10^-6	0,0432	0,0619	0,4111	0,5889	0,0293
9	5,7	3,63*10^-6	6,37*10^-6	0,0334	0,0744	0,3097	0,6903	0,0298
10	5,8	0,65*10^-6	9,35*10^-6	0,0060	0,1091	0,0522	0,9478	0,0304
11	5,8	0	10,0*10^-6	0,0000	0,1167	0,0000	1,0000	0,0304

Sprawdzam addytywność parachory P względem ułamka molowego:

według tego wzory obliczam wartości parachory teoretyczne (P_c = 4,30*10^-5 [J^1/4*m^5/2/mol]; P_d = 3,65*10^-5 [J^1/4*m^5/2/mol]).

Wartości eksperymentalne dla roztworów obliczam z zależności:

gdzie: M - średnia masa molowa dla roztworu, M = M_cx_c + M_dx_d; σ - napięcie powierzchniowe roztworu; d - gęstość roztworu.

L.p.	Gęstość roztworu [kg/m3] (tablicowa)	Ułamek molowy cykloheksanu	Ułamek molowy 1,4-dioksanu	Napięcie powierzch-niowe roztworów [J/m2]	Parachora roztworów (eksperymentalna)	Addytywność parachory (tablicowa)	Błąd procentowy [%]
1	773,7	1,0000	0,0000	0,0267	4,40*10^-5	4,30*10^-5	2,32
2	794,5	0,9521	0,0479	0,0267	4,36*10^-5	4,22*10^-5	3,32
3	805,5	0,9041	0,0959	0,0272	4,35*10^-5	4,18*10^-5	4,07
4	816,8	0,8072	0,1928	0,0277	4,29*10^-5	4,14*10^-5	3,62
5	828,4	0,7095	0,2905	0,0277	4,21*10^-5	4,11*10^-5	2,43
6	840,4	0,6110	0,3890	0,0283	4,14*10^-5	4,07*10^-5	1,72
7	852,7	0,5115	0,4885	0,0288	4,06*10^-5	4,04*10^-5	0,49
8	865,3	0,4111	0,5889	0,0293	3,98*10^-5	4,00*10^-5	0,50
9	878,0	0,3097	0,6903	0,0298	3,89*10^-5	3,97*10^-5	2,01
10	891,0	0,0522	0,9478	0,0304	3,64*10^-5	3,94*10^-5	7,61
11	1028,6	0,0000	1,0000	0,0304	3,58*10^-5	3,65*10^-5	1,92

Sprawdzam poprawność wskazanej przez prowadzącego metody przewidywania napięcia powierzchniowego:

Równanie Sporowa - Prausnitza:

gdzie: A - średnia wartość powierzchni objętej przez cząsteczki tworzące układ,
gdzie: V - objętość molowa składnika, (V_c = 1,09*10^-4 [m³/mol], V_d = 8,57*10^-4 [m³/mol]); N₀ - liczba Avogadra.

L.p.	Napięcie powierzch-niowe roztworów [J/m2]	Napięcie powierzchniowe ze wzoru Sporowa-Prausnitza	Błąd procentowy [%]
1	0,0267	0,0244	9,42
2	0,0267	0,0252	5,95
3	0,0272	0,0256	6,25
4	0,0277	0,0260	6,54
5	0,0277	0,0264	4,92
6	0,0283	0,0268	5,60
7	0,0288	0,0272	5,88
8	0,0293	0,0277	5,78
9	0,0298	0,0281	6,05
10	0,0304	0,0286	6,29
11	0,0304	0,0330	7,88

4. Wnioski:

Jak wynika z uzyskanych danych, zachowana jest na ogół bardzo dobrze addytywność parachory. Odstępstwo wartości na podstawie addytywności znalezionej doświadczalnie tylko w jednym przypadku przekracza 7 %. Wartości napięcia powierzchniowego zachowują się podobnie do wartości parachory, chociaż wartości znacznie odbiegają od wartości uzyskanych teoretycznie ze wzoru Sporowa-Prausnitza. Zależność napięcia powierzchniowego od ułamka molowego jest zależnością prostoliniową.

2

---