POLITECHNIKA GDAŃSKA
WYDZIAŁ BUDOWNICTWA LĄDOWEGO
KATEDRA MECHANIKI BUDOWLI
LABORATORIUM Z
MECHANIKI BUDOWLI
I WYTRZYMAŁOŚCI MATERIAŁÓW
TEMAT ĆWICZENIA :
WYZNACZENIE ŚRODKA ZGINANIA
Wykonali:
Kraczkowski Tomasz
Gabryelewicz Michał
Czynsz Jacek
Szczegielniak Mirosław
WILiS, sem IV
I. Opis doświadczenia
Celem ćwiczenia jest wyznaczenie środka zginania dwóch cienkościennych belek wspornikowych.
W doświadczeniu nr 1 badaliśmy cienkościenną belkę o przekroju rurowym a doświadczeniu nr 2 o przekroju kątowym.
II. Przebieg doświadczenia
W obu przypadkach przebieg doświadczenia polegał na:
Ustawienie nie obciążonej szalki przymocowanej do czoła belki w punkcie zerowym;
Odczytaniu pomiarów z czujników zegarowych;
Obciążenie szalki odważnikami (o masie 4 kg);
Przesuwnie obciążonej szalki w przedziale <-40mm ; 40mm> , co 10mm odczytując wskazania czujników zegarowych;
Zdjęcie odważników i ponowne odczytanie wartości w punkcie zerowym.
III. Wyniki pomiarów
Wzory:
a) średnie odczyty początkowe:
fL0=0,5x(fL1+fL2) fP0=0,5x(fP1+fP2)
b) ugięcia punktów i kąty skręcenia
uL= fL-fL0 uP= fP-fP0
Φ=( uL- uP)/a
Doś 1:
|
fL |
fP |
Odczyt początkowy |
2,98 |
4,94 |
Odczyt końcowy |
3,01 |
4,92 |
Srednia: |
2,995 |
4,93 |
Tabela pomiarowa 1
Położenie siły [mm] |
Wskazania czujników |
Ugięcie punktów |
Kąt skręcenia Φ |
||
|
Lewego fL |
Prawego fP |
Lewego uL |
Prawego uP |
|
-40 |
1,45 |
5,71 |
-1,545 |
0,78 |
-0,11625 |
-30 |
1,8 |
5,36 |
-1,195 |
0,43 |
-0,08125 |
-20 |
2,12 |
5,03 |
-0,875 |
0,1 |
-0,04875 |
-10 |
2,43 |
4,73 |
-0,565 |
-0,2 |
-0,01825 |
0 |
2,995 |
4,93 |
|
|
|
10 |
3,01 |
4,06 |
0,015 |
-0,87 |
0,04425 |
20 |
3,4 |
3,79 |
0,405 |
-1,14 |
0,07725 |
30 |
3,72 |
3,48 |
0,725 |
-1,45 |
0,10875 |
40 |
4,03 |
3,17 |
1,035 |
-1,76 |
0,13975 |
Dos 2.
|
fL |
fP |
Odczyt początkowy |
2 |
4 |
Odczyt końcowy |
2,02 |
3,99 |
Srednia: |
2,01 |
3,995 |
Tabela pomiarowa 2
Położenie siły [mm] |
Wskazania czujników |
Ugięcie punktów |
Kąt skręcenia Φ |
||
|
Lewego fL |
Prawego fP |
Lewego uL |
Prawego uP |
|
-40 |
1,07 |
4,76 |
-0,94 |
0,765 |
-0,08525 |
-30 |
1,25 |
4,56 |
-0,76 |
0,565 |
-0,06625 |
-20 |
1,45 |
4,35 |
-0,56 |
0,355 |
-0,04575 |
-10 |
1,64 |
4,14 |
-0,37 |
0,145 |
-0,02575 |
0 |
2,01 |
3,995 |
|
|
|
10 |
2,03 |
3,73 |
0,02 |
-0,265 |
0,01425 |
20 |
2,24 |
3,52 |
0,23 |
-0,475 |
0,03525 |
30 |
2,43 |
3,33 |
0,42 |
-0,665 |
0,05425 |
40 |
2,61 |
3,13 |
0,6 |
-0,865 |
0,07325 |
IV Obliczenia teoretyczne
a)Przekrój rurowy
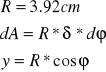
Moment statyczny:
Sz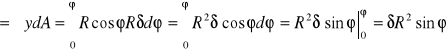
Rówanie naprężeń:
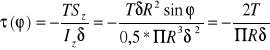
Równanie sumy momentów wszystkich sił względem punktu O:
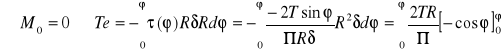
Dla φ=Π otrzymamy
![]()
Zatem otrzymamy:
![]()
b)Przekrój kątowy
![]()
[cm]
![]()
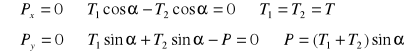
Zatem:
![]()
z warunku:
a![]()
![]()
dla![]()
![]()
V. Porównanie wyników
|
Wartość teoretyczna [cm] |
Wartość doświadczalna [cm] |
Przekrój rurowy |
-4,99 |
|
Przekrój kątowy |
5,3 |
|
VI. Położenie środka ciężkości
a)przekrój rurowy![]()
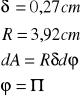
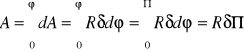
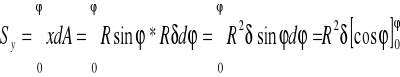
![]()
Zatem:
![]()
![]()
C(xc;yc)=C(-2,496 cm; 0 cm)
b)przekrój kątowy
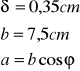
![]()
![]()
![]()
![]()
C(xc;yc)=C(2,652 cm; 0 cm)
VII.
Kąt skręcania dla przypadku obciążenia siła przyłożoną w środku ciężkości
przekrój rurowy
C(-2,495 ; 0)
przekrój kątowy
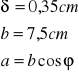
Wyszukiwarka
Podobne podstrony:
plik (80) ppt
80 307 POL ED02 2001
80
80, 81
Audi 80 Cabriolet
HF 91110 80 Amp Inverter Arc Welder
OPONY - oznaczenia, AUDI 80 B4
w 80 dni dookola swiata - test, Lektury SP scenariusze lekcji
doktryna 80-63, Zajęcia WSOWL, OPBMR
Karta operacyjna 80, Politechnika Lubelska, Studia, Studia, wszystkie, Uczelnia, Technologia Maszyn,
80 81
79 80
OLYMPUS µ [mju] III 80 instrukcja obsługi
och srod wykl 5 lata 80 pl, polit ekol panstwa
i 80 id 208512 Nieznany
A 80
żuraw 80
10 1995 79 80
79 80
więcej podobnych podstron