Ćwiczenie nr 2. (2 godz.)

2. Równania stanu gazu doskonałego i rzeczywistego.

• Obliczenia stechiometryczne dla reakcji chemicznych z udziałem reagentów gazowych.

• Obliczenia stechiometryczne dla złożonych reakcji chemicznych z uwzględnieniem reagentów stałych, ciekłych i gazowych.

PRAWA GAZOWE

Materia może występować w różnych stanach skupienia. W porównaniu ze stanem stałym lub ciekłym materii, stan gazowy charakteryzuje się bardzo dużym współczynnikiem ściśliwości, a także brakiem sprężystości i uporządkowania cząsteczek. Różne gazy zachowują się podobnie, a stan fizyczny każdego gazu określają następujące parametry:

1. ilość (w molach) n (lub masa m oraz masa molowa M, przy czym n= m/M),

2. objętość V (cm³, dm³, l),

3. ciśnienie p (Pa),

4. temperatura T (K, °C).

Gaz doskonały

W celu wytłumaczenia prawie jednakowego zachowania się gazów, teoria kinetyczna wprowadziła pojęcie gazu doskonałego, przyjmując następujące założenia, a mianowicie:

• • cząsteczki gazu są tak małe, że można je uważać za punkty materialne,

• • pomiędzy cząsteczkami gazu nie występują siły wzajemnego przyciągania ani odpychania,

• • cząsteczki gazu poruszają się stale i bezładnie po torach prostoliniowych, zderzając się ze sobą i ściankami naczynia, w którym się znajdują,

• • zderzenia cząsteczek gazu są doskonale sprężyste,

• • średnia energia kinetyczna cząsteczek jest proporcjonalna do temperatury gazu w skali Kelvina.

W praktyce mamy do czynienia z gazami rzeczywistymi, które mają określone wymiary a pomiędzy cząsteczkami gazu występują różnego rodzaju oddziaływania. Gazy rzeczywiste, nie spełniające założeń gazu doskonałego, można doprowadzić do takiego stanu, że jego własności będą zbliżone do własności gazu doskonałego. Można to osiągnąć przez dostateczne obniżenie ciśnienia lub podwyższenie temperatury. Im większe natomiast jest ciśnienie i niższa temperatura, tym większe są odstępstwa gazu rzeczywistego od podanych niżej praw gazu doskonałego. Co ciekawe, prawa gazowe zostały najpierw ustalone doświadczalnie dla gazów rzeczywistych, mimo że rzeczywiste gazy podlegają im jedynie w ograniczonym zakresie. Najlepiej prawa te są spełnione w wysokich temperaturach pod niskim ciśnieniem. Charakter zachowań gazu doskonałego w zależności od ciśnienia, temperatury i zajmowanej objętości opisują prawa gazu doskonałego (często nazywane krótko prawami gazowymi). Są to następujące prawa gazowe:

• • prawo izotermy (prawo Boyle'a-Mariotta)

• • prawo izobary (prawo Gay-Lussaca)

• prawo izochory (prawo Charlesa)

Prawo Boyle'a - Mariotte'a (1672)

W. R. Boyle (1660) i niezależnie E. Mariotte (1676) w celu zbadania zależności objętości gazu od ciśnienia skonstruowali urządzenie w którym w U-rurce zamknęli nad rtęcią pewną ilość gazu, która była poddawana ciśnieniu w wyniku dodawania nowych porcji rtęci. Ciśnienie wywierane na gaz było równe sumie ciśnienia atmosferycznego P₀, oraz różnicy w wysokości słupa rtęci Δh (P=P0+Δh). Stwierdzili oni, że iloczyn objętości V i ciśnienia p gazu jest zawsze wielkością stałą.

Prawo Boyle'a-Mariotte'a dotyczy zatem zależności zmiany objętości gazu przez zmianę jej ciśnienia w stałej temperaturze i mówi, że objętość gazu jest odwrotnie proporcjonalna do ciśnienia w stałej temperaturze. Zatem w trakcie przeprowadzania procesu izotermicznego iloczyn ciśnienia i objętości jest stały; ciśnienie i objętość są w tym procesie wielkościami odwrotnie proporcjonalnymi.

dla T = const n = const

wówczas:

p

p₁

Izoterma gazu doskonałego

p₂

V₁ V₂

V

Prawa Boyle'e - Mariotte'a było uzyskane pierwotnie na drodze empirycznej - jako uogólnienie danych doświadczalnych. Twierdzenie to jest prawdziwe wyłącznie dla gazu doskonałego. Odkrył je w 1662 r. irlandzki fizyk Robert Boyle (1627-91) i w krajach anglosaskich nazywane jest prawem Boyle'a. W Polsce znane jest jako prawo Boyle'a-Mariotte'a, od nazwiska Edmégo Mariotte'a (1620-84), który odkrył je niezależnie w 1676 r.

Wykresy zależności ciśnienia, temperatury i objętości dla procesów izotermicznych

Przykład 2.1

Pewna masa gazu zajmuje objętość 250 cm³ pod ciśnieniem 300 hPa. Oblicz jej objętość pod ciśnieniem 1000 hPa w tej samej temperaturze.

V₁/V₂ = p₂/p₁ ⇒ V₂ = V₁·p₁/p₂ = 250·300/1000 = 75 cm³

Prawo Charlesa i Gay-Lussaca

Prawo to odkrył, na podstawie doświadczeń rozpoczętych ok. 1787 r., francuski uczony Jacques Alexandre Charles (1746-1823), ale właściwie sformułował je, dzięki bardziej dokładnym wynikom, które opublikował w 1802 r., Francuz Louis Joseph Gay-Lussac (1778-1850) i dlatego jest nazywane prawem Charles'a i Gay-Lussaca.

Prawo to opisuje:

zależność objętości i ciśnienia gazu od temperatury (prawo izobary Gay-Lussaca):

dla p = const

gdzie: V_T - objętość gazu w temperaturze T ^oC

V₀ - objętość gazu w temperaturze 0 ^oC

α - współczynnik rozszerzalności gazu α = 1/273,15

Rozwiązaniem równania jest zależność:

dla (T₀ = 273,15 K = 0 °C)

czyli V/T = const

lub dla dwóch temperatur T₁ i T₂

czyli:

p₂

V

p₁

V₂

Izobara gazu doskonałego

V₁

T₁ T₂ T

zależność ciśnienia gazu od temperatury dla stałej objętości (prawo izochory, Charles'a)

dla V = const

gdzie: p - ciśnienie gazu w temperaturze T ^oC

p₀ - ciśnienie gazu w temperaturze 0 ^oC

β - współczynnik prężności gazu β = 1/273,15

Rozwiązaniem równania jest zależność:
(T₀ = 273,15 K = 0 °C)

czyli p/T = const

lub dla dwóch temperatur T₁ i T₂

czyli:

V₂

p

V₁

p₂

Izochora gazu doskonałego

p₁

T₁ T₂ T

Przykład 2.2

W temperaturze 300 K i pod ciśnieniem 746 kPa gaz zajmuje objętość 0,5 dm³ . Jaką objętość zajmie gaz w temperaturze 265 K? Założenie, nie ma zmiany ciśnienia.

V₁/V₂ = T₁/T₂ ⇒ V₂ = 0,5·265/300 = 0,44 dm³

Prawo prostych stosunków objętościowych Gay-Lussaxa (1809)

Prawo to mówi, że objętość gazów (mierzona w p,T = const) reagujących ze sobą lub tworzących się w reakcji chemicznej mają się do siebie w prostych stosunkach liczbowych.

Pod pojęciem warunków normalnych rozumie się takie warunki, dla których temperatura wynosi 0 °C (273,15 K), zaś ciśnienie równa się 1 atmosferze lub 760 mm Hg czyli 101325 Pa.

W celu przeliczenia objętości gazu znajdującego się w warunkach różniących się od normalnych na objętość w warunkach normalnych można posłużyć się równaniem:

Przykład 2.3

Jaka objętość w warunkach normalnych będzie zajmował gaz obecnie zajmujący objętość 0,5 m³ pod ciśnieniem 1100 mm Hg i w temperaturze 10 °C.

p₀·V₀/T₀ = p₁·V₁/T₁ ⇒ V₀ = p₁·V₁·T₀/p₀·T₁ = 1100·0,5·273,15/760·283,15 = 0,7 m³

Prawo Avogadra

Według tego prawa jednakowe objętości różnych gazów w tej samej temperaturze i pod tym samym ciśnieniem zawierają jednakową liczbę cząsteczek.

MOL jest to taka liczność materii, która zawiera tyle elementarnych jednostek, ile jest atomów węgla w 12 g węgla ¹²C. Te elementarne jednostki musza być określone i mogą to być: atom, cząsteczka, jon, elektron, foton itp. bądź tez określona grupa takich jednostek.

Ponieważ j.m.a (1/12 masy izotopu ¹²C) wyrażona w gramach wynosi 1,66∙10^-24 g, to jeden atom ¹²C ma masę 12∙1,66∙10^-24 = 1,99∙10^-23 g. W 1 molu ¹²C tj. w 12 g znajduje się:

Jest to tzw. liczba Avogadra (N_A), która wg definicji jest równa liczbie atomów węgla zawartych w 12 g izotopu węgla ¹²C. Do podstawowych obliczeń chemicznych można stosować przybliżoną wartość 6,02∙10²³.

Stwierdzono, że objętość molowa gazu doskonałego w warunkach normalnych wynosi 22,415 dm³. Gazy rzeczywiste wykazują jednakże pewne odchylenia od podanej wartości, zaś do celów obliczeniowych przyjmuje się, że objętość molowa dowolnego gazu rzeczywistego w warunkach normalnych wynosi 22,4 dm³/mol.

Równanie Clapeyrona (stanu gazu doskonałego)

Równanie to podaje zależność pomiędzy ciśnieniem, objętością, temperaturą a liczbą moli gazu i można je wyprowadzić z pozostałych praw gazowych.

gdzie: p - ciśnienie gazu [Pa]

V - objętość gazu [m³]

n - liczba moli substancji [mol]

T - temperatura [K]

R - uniwersalna stała gazowa 8.314 J/mol∙K

Równanie van der Waalsa (stanu gazu rzeczywistego)

Doświadczenia wykazały, iż zachowanie się gazów przy wysokich ciśnieniu i niskiej temperaturze może odbiegać nieco od tego przewidzianego prawem Boyle'a - Mariotte'a (PV=const). Na podstawie tychże odchyleń gazów holenderski naukowiec J.D. van der Waals zaproponował skorygowaną wersję prawa Boyle'a - Mariotte'a. Stwierdził on bowiem, że zaobserwowane ciśnienia są zazwyczaj mniejsze od przewidzianych, a objętości większe. Jak widać równanie van der Waalsa

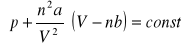
jest modyfikacją prawa Boyle'a - Mariotte'a, wzbogaconą o poprawkę n²a/V² dodawaną do obserwowanego ciśnienia i poprawkę nb odejmowana od obserwowanej objętości (n równa się liczbie moli w próbce, a i b są stałymi charakterystycznymi dla danego gazu). Stała a zależy od oddziaływania wzajemnego cząsteczek, b zaś od objętości cząsteczki. Wobec powyższego, równanie stanu gazu rzeczywistego według van der Waalsa ma postać:

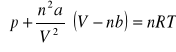
Przykład 2.4

Oblicz ciśnienie wywołane przez 0,250 mol ditlenku węgla zajmującego objętość 0,275 dm³ w temperaturze 100 °C i porównaj tę wartość z wartością przewidzianą dla gazu doskonałego.

a = 0,364 m⁶·Pa/mol²

b = 4,27·10^-5 m³/mol

(p+n²·a/V²)·(V-nb) = nRT ⇒ p = nRT/(V-nb)-n²a/V² =

= 0,250·8,3143·373,15/(0,275·10^-3-0,250·4,27·10^-5)-0,250²·0,364/0,275²·10^-6 =

= 2632000 Pa = 2,632 MPa (w rzeczywistości zaobserwowana wartość ciśnienia)

pV = nRT ⇒ p = nRT/V = 0,250·8,3143·373,15/0,275·10^-3 = 2820000 Pa = 2,820 MPa

Zadania do samodzielnego rozwiązania:

1. Jaka objętość w warunkach normalnych zajmuje 1 mol, a jaką 63,9 g chlorowodoru (HCl)? Warunki normalne: p = 101325 Pa = 1 atm;

T = 273,15 K = 0 °C.1 J = kg·m²·s^-2 , 1 Pa = kg·m^-1·s^-2.

2. Butla ze sprężonym tlenem wykazuje ciśnienie 140 atm w temp. 18 °C. Jak zmieni się ciśnienie (przy założeniu gazu doskonałego), gdy temperatura pomieszczenia wzrośnie do 25 °C?

3. Butelka o pojemności 1 dm³ wypełniona helem pod ciśnieniem 102358 Pa rozbiła się w pokoju o wymiarach 4x4x3 m. Przy założeniu zachowania się helu jak gazu doskonałego, jakie będzie jego ciśnienie w pokoju.

4. Graniczna dopuszczalna zawartość trującego gazu H₂S wynosi 10 mg/m³. Jakiemu to odpowiada ciśnieniu? Przyjmij zachowanie się gazu jak doskonałego w temperaturze 20 °C.

5. Licznik gazowy, który nie kompensował zmian temperatury gazu, wykazał w lutym przepływ 1000 m³. W tym samym miesiącu średnia temperatura wynosiła -5 °C. W sierpniu, przy temperaturze średniej równej 30 °C ten sam licznik wykazał również zużycie 1000 m³ gazu. Obliczyć procentową różnicę faktycznego zużycia gazu w lutym i sierpniu przy założeniu, że ciśnienie nie zmieniło się.

6. W zbiorniku o objętości 2,5 dm³ znajduje się wodór pod ciśnieniem 1 hPa. Ile cząsteczek wodoru znajduje się w tym zbiorniku, jeżeli temperatura gazu wynosi 0 °C?

7. W wyniku rozkładu 120 g węglanu wapnia (CaCO₃) otrzymano pewną ilość ditlenku węgla, który w warunkach normalnych zajął objętość 26880 cm³. Pod jakim ciśnieniem ta sama ilość ditlenku węgla zajmie objętość 20 dm³, jeżeli temperatura pozostanie bez zmian?

8. Podczas spalania metanu (CH₄) powstaje ditlenek węgla i para wodna. Jaki jest stosunek między objętościami gazów biorących udział w reakcji, jeżeli objętości te są mierzone w jednakowych warunkach.

9. Termiczny rozkład ditlenku ołowiu zachodzi zgodnie z równaniem:

3PbO₂ →Pb₃O₄+O₂. Obliczyć objętość wydzielonego tlenu w warunkach normalnych, jeżeli rozkładowi uległo 180 g PbO₂. Jaką objętość zajmuje ta masa tlenu w temperaturze 26,85 °C i pod ciśnieniem 2034 hPa?

10. W warunkach normalnych (T = 273,15 K i p = 1013,25 hPa) 5 moli wodoru zajmuje objętość 0,112 m³. Pod jakim ciśnieniem ta sam ilość wodoru zajmie objętość 20 dm³, jeżeli temperatura pozostanie bez zmian?

11. Obliczyć masę molową gazu, którego 0,903 g zajmuje w warunkach normalnych objętość 250 cm³.

12. Obliczyć, ile gram tlenku (II) węgla (IV) można otrzymać z 30 g węglanu (IV) wapnia (II) w wyniku reakcji z kwasem solnym. Jaką objętość zajmie wydzielony gaz w warunkach normalnych?

13. Ile gramów wodoru przereaguje z 6 dm³ tlenu (warunki normalne)?

14. Ile dm³ wodoru i ile dm³ azotu odmierzonych a) w warunkach normalnych, b) w temperaturze 298 K pod ciśnieniem 976 hPa, należy zmieszać w celu przygotowania substratów do syntezy 200 g amoniaku?

15. Benzyna jest mieszanina ponad stu różnych węglowodorów, przy czym heptan (C₇H₁₆) odzwierciedla średni skład chemiczny benzyny. Zakładając, że pełne spalenie heptanu przebiega zgodnie z reakcją:
    

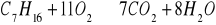
Obliczyć:

1. ile wody powstanie w wyniku spalenia 20 litrów benzyny?

2. Ile zużyje się przy tym tlenu (w g i dm³)?

3. Ile suchego lodu (stały dwutlenek węgla) można otrzymać, jeśli reakcja zaszła z 95% wydajnością?

Przyjąć, że gęstość benzyny wynosi 0,78 g/cm³.

7

7

---