Projekt 1
Zbadaj przebieg zmienności i naszkicuj wykres funkcji:![]()
.
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
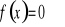
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
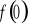
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnej pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnej drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 2
Zbadaj przebieg zmienności i naszkicuj wykres funkcji: ![]()
.
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
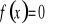
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
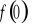
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 3
Zbadaj przebieg zmienności i naszkicuj wykres funkcji: ![]()
.
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
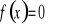
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
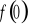
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 4
Zbadaj przebieg zmienności i naszkicuj wykres funkcji: 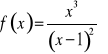
.
Wskazówka:
a) Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
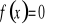
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
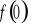
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 5
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
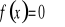
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
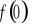
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 8
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
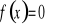
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
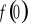
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 10
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
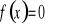
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
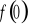
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 11
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
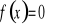
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
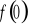
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 12
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :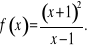
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
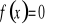
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
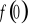
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 13
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
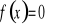
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
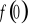
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 14
a) Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
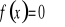
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
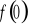
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 15
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
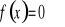
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
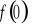
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 16
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :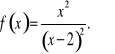
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
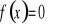
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
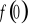
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 17
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
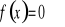
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
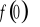
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 18
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
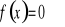
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
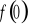
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 19
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
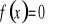
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
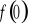
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 20
Zbadaj przebieg zmienności i naszkicuj wykres funkcji :![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
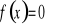
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
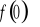
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 21
Zbadaj przebieg zmienności i naszkicuj wykres funkcji:![]()
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
Wyznaczenie dziedziny funkcji.
Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania
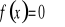
).Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie
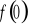
).Sprawdzenie czy funkcja jest parzysta, nieparzysta.
Wyznaczenie asymptot poziomych, pionowych i ukośnych.
Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
Sporządzenie tabelki przebiegu zmienności funkcji.
Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Projekt 22
Zbadaj przebieg zmienności i naszkicuj wykres funkcji: ![]()
.
Wskazówka:
Badanie zmienności funkcji składa się z następujących czynności:
1.Wyznaczenie dziedziny funkcji.
2. Wyznaczenie miejsc zerowych (tzn. rozwiązanie równania ![]()
).
3. Wyznaczenie wartości funkcji w zerze ( tzn. obliczenie ![]()
).
4. Sprawdzenie czy funkcja jest parzysta, nieparzysta.
5. Wyznaczenie asymptot poziomych, pionowych i ukośnych.
6. Obliczenie pochodnych pierwszego rzędu, wyznaczenie punktów krytycznych, przedziałów monotoniczności oraz ekstremów lokalnych.
7. Obliczenie pochodnych drugiego rzędu funkcji, wyznaczenie punktów przegięcia oraz przedziałów jej wklęsłości i wypukłości.
8. Sporządzenie tabelki przebiegu zmienności funkcji.
9. Narysowanie wykresu w układzie współrzędnych OXY na płaszczyźnie.
Wyszukiwarka
Podobne podstrony:
8617
8617
8617
8617
więcej podobnych podstron