Sprawozdanie z ćwiczenia numer 5:

"Konduktometryczne wyznaczanie stałej dysocjacji kwasu mrówkowego HCOOH."

Ze względu na rodzaj nośników prądu jego przewodniki można podzielić na dwie zasadnicze grupy: przewodniki elektronowe, w których nośnikami prądu są elektrony oraz jonowe, gdzie przepływ prądu związany jest z ruchem jonów; roztwory elektrolitów należą do tej drugiej grupy. Zdolnośćprzewodników do przewodzenia prądu charakteryzuje sie przezpodanie ich oporu właściwego,równego liczbowo oporowi sześćianu o boku jednostkowym. W wypadku przewodników elektrolitycznych używa sie najczęściej pojęcia przewodnictwa właściwego.

Wyznaczam stałą naczyńka dla znanego roztworu KCl 0,01M, którego przewodnictwo

właściwe wynosi κ= 0,001413 S

gdzie R jest to odwrotność zmierzonego przewodnictwo roztowru wzorcowego.

k=0,001413*(1/0,00112)=1,1874

Po wyznaczeniu stałej naczyńka obliczam wartość przewodnictwa molowego dla

każdego z badanych roztworów (HCl, NaCl, HCOONa, HCOOH)

Przykładowe obliczenia:

Przewodnictwo właściwe:

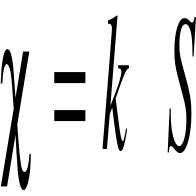
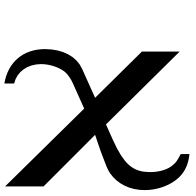
=1,1874 x 0,00119=0,0014 S/cm

Przewodnictwo molowe:

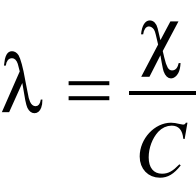
λ=0,001413/0,0625=0,02261 [S*cm²/mol]

HCOOH				HCOONa
C [mol/dm^3]	S [mS]	[S/cm]	λ[S*cm^2/mol]	C [mol/dm^3]	S [mS]	[S/cm]	λ[S*cm^2/mol]
0,0625	1,19	0,001413	0,022608	---	---	---	---
0,03125	0,83	0,000986	0,031537	0,03125	2,1	0,002494	0,079793
0,015625	0,56	0,000665	0,042556	0,015625	1,1	0,001306	0,083593
0,007813	0,38	0,000451	0,057751	0,007813	0,57	0,000677	0,086627
0,003906	0,25	0,000297	0,075998	0,003906	0,3	0,000356	0,091198
0,001953	0,16	0,00019	0,097278	0,001953	0,13	0,000154	0,079038
0,000977	0,09	0,000107	0,109382	0,000977	0,076	0,00009024	0,092367

HCl				NaCl
C [mol/dm^3]	S [mS]	[S/cm]	λ[S*cm^2/mol]	C [mol/dm^3]	S [mS]	[S/cm]	λ[S*cm^2/mol]
0,03125	8,9	0,010568	0,338172	0,03125	2,6	0,003087	0,098792
0,015625	4,9	0,005818	0,372369	0,015625	1,48	0,001757	0,112471
0,007813	2,2	0,002612	0,33435	0,007813	0,76	0,000902	0,115503
0,003906	1,123	0,001333	0,341385	0,003906	0,368	0,000437	0,11187
0,001953	0,567	0,00067	0,342905	0,001953	0,193	0,000229	0,117342
0,000977	0,295	0,00035	0,358529	0,000977	0,096	0,000114	0,116674

Następnie podstawiam pod x wartość 0 i otrzymuję wartość przewodnictwa granicznego

_HCl=0,3459
_NaCl=0,1021
_HCOONa=0,0801.

Korzystając z prawa niezależnego ruchu jonów wyznaczam przewodnictwo graniczne HCOOH

=0,3459+0,0801-0,1021=0,3239

Obliczam wyrażenia 1/λ oraz c₀*λ aby wykreślić wykres:

C	λ	1/λ	C*λ
0,0625	0,022608	44,23	0,001413
0,03125	0,031537	31,71	0,0009855
0,015625	0,042556	23,498	0,000665
0,007813	0,057751	17,316	0,00045
0,003906	0,075998	13,16	0,000297
0,001953	0,097278	10,28	0,00019
0,000977	0,109382	9,142	0,000107

Stałą dysocjacji HCOOH wyznaczam ze wzoru:

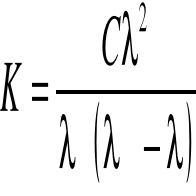
Przykładowe obliczenie:

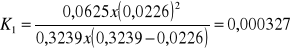
Pozostałe wartości:

K₂=0,000328

K₃=0,000311

K₄=0,000302

K₅=0,000281

K₆=0,000252

K₇=0,000168

K_śr= 0,000281

pK=3,55

Wartość literaturowa to Ka=0,000177 czyli pKa=3,75

Obliczam błąd bezwzględny:

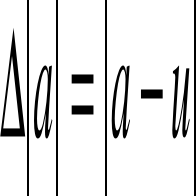
= |-0,2| = 0,2

Obliczam błąd względny:

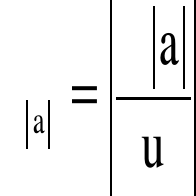
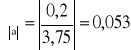
Obliczam błąd procentowy:

Dyskusja wyników:

Otrzymana przez nas wartość stałej dysocjacji kwasu mrówkowego różni się od wartości tablicowej, jednak nie jest to błąd duży. Może on wynikać z niedokładnego przygotowania roztworów lub zbyt krótkiego czasu oczekiwania na ustalenie się wartości S. Błędy mają tendencje malejącą i wydaja sie maleć wraz ze wzrostem rozcieńczenia roztworu.

Równanie kinetyczne i stała szybkości reakcji wyznacza sie na podstawie danych kinetycznych w określonej temperaturze,ponieważ stałej szybkości znacznie wzrasta ze wzrostem temperatury. W sposób przybliżony i orientacyjny można zapisać wpływ temperatury przez podanie tzw, współ.temperaturowego reakcji, czyli stosunku stałej szybkości w temperaturze T+10K do stałej szybkości w temp T K, bardziej dokładnie ujmuje tę zależność równanie Arrheniusa, wg którego:

Log k =B - A/T

W równaniu tym k oznacza stałą szybkości reakcji, A i B stałe charakterystyczne dla danej reakcji, t- temperaturę w skali Kelvina. Wytłumaczenie przyczyn,dla których szybkość reakcji tak znacznie zależy od temperatury daje m.in. teoria zderzeń aktywnych. Wg niej efektywne są tylko te zderzenia, w których biorą udział cząsteczki posiadające energię większą lub równą pewnej granicznej wartości, zwanej energią aktywacji. Można wykazać, że stała A w równaniu Arrheniusarówna jest E_a /2,303R. Wartość energii aktywacji E_a można znaleść ze znanych wartości stałych szybkości k₁ i k₂ wyznaczonych w temp T₁ i T₂. Najczęsciej znajduje sie średnią wartość energii aktywacji dla danego przedziału temperatur(graficznie) z zalęzności log k =f(T^-1).

---