Układ liniowy - odpowiedź i wymuszenie spełniają zasadę:
jednorodności: x(t) -> r(t) => k·x(t) -> k·r(t)
addytywności: (x1(t) -> r1(t) i x2(t) -> r2(t)) => (x1(t) + x2(t)) -> (r1(t) + r2(t))
Obie te zasady składają się na zasadę superpozycji.
PRAWA
Prawo Ohma - natężenie prądu stałego I jest proporcjonalne do całkowitej siły elektromotorycznej w obwodzie zamkniętym lub do różnicy potencjałów (napięcia elektrycznego) między końcami części obwodu niezawierającej źródeł siły elektromotorycznej: I = U / R.
I Prawo Kirchoffa - algebraiczna suma natężeń prądów i(t) we wszystkich gałęziach dołączonych do jednego, dowolnie wybranego węzła obwodu, w każdej chwili czasu jest równa zero.
II Prawo Kirchoffa - algebraiczna suma napięć u(t) na wszystkich elementach tworzących dowolnie wybrane oczko obwodu elektrycznego w każdej chwili czasu jest równa zero.
I Twierdzenie Vashy'ego - do każdej z gałęzi dołączonych do dowolnie wybranego węzła obwodu można włączyć szeregowo idealne, jednakowe, o tych samych zwrotach względem węzła źródła napięciowe nie zmieniając stanu obwodu.
II Twierdzenie Vashy'ego - do każdej z gałęzi stanowiących dowolnie wybrane oczko obwodu można włączyć równolegle idealne, jednakowe, o tych samych zwrotach względem obiegu oczka źródła prądowe nie zmieniając stanu obwodu.
Prawo Joul'a - dla idealnego rezystora zachodzi równość pomiędzy pracą prądu elektrycznego i ilością ciepła wydzieloną na rezystorze.
Zasada zachowania energii - obwód elektryczny (model układu elektrycznego) musi spełniać fundamentalna przyrodnicza zasadę zachowania energii, w myśl której całkowita energia układu odosobnionego jest niezmienna w czasie.
Zasada superpozycji - odpowiedź liniowego obwodu elektrycznego w postaci przebiegu napięć lub prądu w wybranej gałęzi, na zespól działających w obwodzie wymuszeń, jest równa sumie odpowiedzi wywołanych w tej gałęzi przez każde z wymuszeń osobno.
Zasada bilansowania mocy - moc w każdej chwili czasu w odosobnionym obwodzie elektrycznym jest równa zeru
Zasada kompensacji - w obwodzie elektrycznym prądy nie ulegną zmianie, jeżeli w dowolnie wybranej gałęzi obwodu element bezźródłowy zastąpi się idealnym źródłem napięcia równym co do wartości i zwrotu napięciu na danym elemencie, lub idealnym źródłem prądu równym co do wartości i zwrotu prądowi w danym elemencie.
Zasada równoważności obwodów - dwa obwody są równoważne z punktu widzenia zacisków, jeżeli związki pomiędzy napięciami i prądami zaciskowymi są w obu układach identyczne.
Zasada równoważności elementów - dwa elementy są równoważne, jeżeli równe macierze wymuszeń wywołują równe macierze odpowiedzi.
Twierdzenie Thevenina - każdy dwójnik źródłowy jest równoważny gałęzi zawierającej idealne źródło napięcia o wartości równej napięciu dwójnika w stanie jałowym i połączonego z nim szeregowo idealnego rezystora o rezystancji równej rezystancji wewnętrznej dwójnika.
Twierdzenie Nortona - każdy dwójnik źródłowy jest równoważny gałęzi zawierającej idealne źródło prądu o wartości równej prądowi zwarcia dwójnika i połączonego z nim równolegle idealnego rezystora o konduktancji równej konduktancji wewnętrznej dwójnika.
Rezystancja wewnętrzna (konduktancja wewnętrzna) - jest równa rezystancji (konduktancji) zastępczej dwójnika bezźródłowego otrzymanego po wyzerowaniu w wewnętrznej strukturze dwójnika wszystkich autonomicznych źródeł energii (idealne źródła napięciowe zwarte, prądowe rozwarte).
Zasada przekształcania układu:
Zasada wzajemności - jeżeli idealne źródło napięcia włączone w obwód wejściowy na wyjściu wywoła prąd I, to włączone w obwód wyjściowy na wejściu również wywoła prąd I równy co do wartości (niekoniecznie znaku).
Twierdzenie Parsevala - wartość średnia okresu iloczynu dwóch funkcji okresowych jest równa sumie (-∞;∞) szeregu nieskończonego, którego wyrazami są współczynniki rozwinięcia wykładniczego jednej z tych funkcji przez współczynniki sprzężone rozwinięcia drugiej z tych funkcji.
Splot - jest to funkcja: 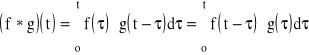
Twierdzenie Borela - transformata splotu funkcji opisujących sygnał jest równa iloczynowi transoframat każdej z tych funkcji z osobna.
MOC I PRACA
Jeżeli na zaciskach elementu obwodu, w których występuje prąd, istnieje napięcie, to moc pobierana przez ten element określana jest wzorem: P(t) = I(t)·U(t).
Energia pobierana przez ten element (praca prądu elektrycznego):
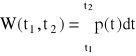
Dopasowanie energetyczne odbiornika do źródła - taki wybór parametrów źródła, dla których moc użyteczna będzie maksymalna. Zachodzi pod warunkiem Ro = Rw (η = 0,5) dla prądu stałego i Zo = Zw* dla prądu zmiennego.
Rodzaje mocy:
Po - moc pobierana przez odbiornik
Pw - moc oddawana przez źródło
Pu = Po + Pw
P(t) = u(t) ·i(t) - moc chwilowa
S = U·I* = P + jQ - moc pozorna
P = Re (S) = U·I·cos(<U,I) - moc czynna
Q = Im (S) = U·I·sin(<U,I) - moc bierna
Sprawność:
a) w schemacie napięciowym:
ηu = Po / Pu
Po = Ro·I2
Pw = Rw·I2
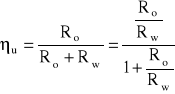
Pmax = U2 / 4·Rw
b) w schemacie prądowym:
ηi = Po / Pu
Po = Go·I2
Pw = Gw·I2
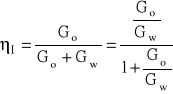
c) dla prądu zmiennego:
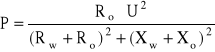
ELEMENTY I UKŁADY NIELINIOWE
Obwód elektryczny jest nieliniowy, jeżeli chociaż jednego z jego elementów jest nieliniowy, tzn. jego charakterystyka prądowo - napięciowa I = f(U) lub U = g(I) jest nieliniowa (nie można opisać jej równaniem prostej).
Metody rozwiązywania obwodów nieliniowych:
a) metoda charakterystyki łącznej:
- Dla obwodu nieliniowego składającego się z elementów połączonych szeregowo, podstawa do dokonania transfiguracji wykreślnej (określenia charakterystyki zastępczej) jest II prawo Kirchoffa: U = U1 + U2 = Fr1(i) + Fr2(i) = Fr(i)
- Dla obwodu nieliniowego składającego się z elementów połączonych równolegle, podstawa do dokonania transfiguracji wykreślnej (określenia charakterystyki zastępczej) jest I prawo Kirchoffa: I = I1 + I2 = ϕr1(u) + ϕr2(u) = ϕr(u)
b) metoda przecięcia charakterystyk - Jeżeli dana jest wartość napięcia zastępczego, bądź prądu zasilającego obwód o znanych charakterystykach nieliniowych to istnieje możliwość określenia punktu pracy obwodu bez wyznaczania charakterystyki łącznej.
METODY ANALIZY OBWODÓW ELEKTRYCZNYCH
Analiza obwodu polega na określeniu rozpływu prądów we wszystkich jego gałęziach i rozkładu napięć na wszystkich jego elementach.
Graf obwodu - jest to zbiór punktów odpowiadających węzłom obwodu i łączących je krzywych regularnych odpowiadających gałęziom.
Drzewo grafu - jest podgraf grafu obwodu złożony z najmniejszej liczby dowolnie wybranych gałęzi łączących wszystkie węzły. Każde drzewo grafu obwodu o „w” węzłach zawiera „w-1” gałęzi.
Gałęzie łączące (zamykające) - pozostałe po wyborze do drzewa grafu gałęzie.
Graf skierowany - graf obwodu z zaznaczonymi w sposób dowolny zwrotami prądów gałęziowych.
Metoda praw podstawowych - poszukujemy Ig i Ug, ale dysponując prawem Ohma i prawami Kirchoffa poszukujemy tylko „g” zmiennych (dla Ig liczba zmiennych niezależnych równa jest liczbie gałęzi zamykających, dla Ug - liczbie gałęzi drzewa). Po uproszczeniach i otrzymaniu równań niezależnych stanowi ona metodę węzłową lub oczkową zależnie od poszukiwanych zmiennych.
Metoda oczkowa - poszukiwane prądy gałęziowe Ig.
Metoda węzłowa - poszukiwane napięcia międzywęzłowe Ug.
Metoda zastępczego generatora - wykorzystanie dopasowania energetycznego odbiornika do źródła w celu wyznaczenia parametrów nieznanego elementu.
WIELOBIEGUNNIKI
Każdy element (układ liniowy) można rozpatrywać jako element wielozaciskowy.
Z każdym zaciskiem wielobiegunnika związany jest prąd zaciskowy Ik oraz potencjał Uk określone względem pewnego zacisku odniesienia nie należącego do tego elementu.
Każdy prąd Ik zależy liniowo tylko od różnic napięć pomiędzy wszystkimi zaciskami.
Wrota (para, brama) - dwie końcówki wielobiegunnika k-ta i k+1, dla których jest spełniony warunek Ik = Ik+1.
Macierz admitancyjna: I = Y·U + I0
Element macierzy admitancyjnej - yi,j = (Ii - Ii0) / Uj - jest to różnica prądów Ii oraz Ii0 płynących przez i-ty zacisk w przypadku, gdy uzi8emiono wszystkie zaciski, a do
j-tego zacisku doprowadzono napięcie względem uziemienia.
Suma elementów w każdym wierszu oraz w każdej kolumnie macierzy admitancyjnej jest równa zero. Jej wyznacznik również jest równy zero.
CZWÓRNIKI
Czwórnik (dwuwrotnik) - układ elektryczny czterokońcówkowy o dwóch parach wrót.
Stan czwórnika jest w pełni opisany przez cztery funkcje: dwa napięcia U1(t), U2(t) oraz dwa prądy I1(t), I2(t).
Czwórnik jest liniowy, jeśli spełnia zasadę superpozycji.
Czwórnik jest opisany równaniami macierzowymi:
[U1 U2]T = Z·[I1 I2]T - macierz impedancyjna
[I1 I2]T = Y·[U1 U2]T - macierz admitancyjna
[U1 I2]T = H·[I1 U2]T - macierz hybrydowa
[I1 U2]T = G·[U1 I2]T - macierz hybrydowa odwrotna
[U1 I1]T = A·[U2 -I2]T - macierz łańcuchowa
[U2 I2]T = B·[U1 -I1]T - macierz łańcuchowa odwrotna
Czwórnik prawidłowy posiada wszystkie macierze charakterystyczne. Warunkiem koniecznym jest, aby istniała nieosobliwa macierz o wszystkich elementach niezerowych.
Czwórnik zdegenerowany (nieprawidłowy posiada więcej niż jedną a mniej niż sześć macierzy charakterystycznych.
Czwórnik zerowy posiada jedną macierz o wszystkich elementach równych zero.
Czwórnik bilateralny posiada obie macierze łańcuchowe.
Czwórnik unilateralny posiada jedną z macierzy łańcuchowych.
Czwórnik nielateralny nie ma żadnej macierzy łańcuchowej.
Czwórniki są równoważne, jeżeli ich odpowiednie macierze są sobie równe.
Czwórnik jest pasywny, jeżeli w każdej chwili czasu dla każdej pary napięć i prądów zaciskowych moc czynna pobierana przez wrota czwórnika jest nieujemna.
Czwórnik jest aktywny, jeżeli istnieją takie wartości napięć i prądów zaciskowych, dla których moc czynna pobierana przez wrota czwórnika jest ujemna.
Czwórnik jest odwracalny, jeżeli spełnia zasadę wzajemności.
Czwórnik jest symetryczny, jeżeli zamiana miejscami wrót pierwotnych i wtórnych czwórnika nie spowoduje zmiany odpowiednich wartości zaciskowych. Warunkiem koniecznym symetryczności czwórnika jest jego odwracalność.
Parametry robocze czwórnika:
Z1 = U1 / I1 - impedancja wejściowa pierwotna (przy podłączeniu dwójnika źródłowego do wrót pierwotnych czwórnika).
Z2 = U2 / I2 - impedancja wyjściowa wtórna (przy obciążeniu wrót wtórnych odbiornikiem dla napięcia wrót wtórnych czwórnika w stanie jałowym i prądu zwarcia wrót wtórnych).
Poza tym definiuje się impedancję wyjściową pierwotną (obciążenie wrót pierwotnych odbiornikiem) i impedancję wejściową wtórną (podłączenie dwójnika źródłowego do wrót wtórnych czwórnika) oraz odpowiadające im admitancję. Wielkości te określane są mianem immitancji.
Transmitancje (przy podłączeniu dwójnika źródłowego do wrót pierwotnych, a obciążenia do wrót wtórnych czwórnika) - dotyczą granicznych stanów pracy czwórnika:
- napięciowa (wzmocnienie napięciowe): Ku = U2 / U1
- prądowa (wzmocnienie prądowe): Ki = -I2 / I1
- napięciowo - prądowa (impedancja przejściowa): Kui = U2 / I1
- prądowo - napięciowa (admitancję przejściowa): Kiu = -I2 / U1
- skuteczna napięciowa (skuteczne wzmocnienie napięciowe): 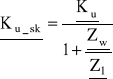
- skuteczna prądowa (skuteczne wzmocnienie prądowe): 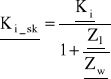
- wzmocnienie mocy: 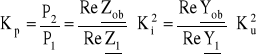
- skuteczne wzmocnienie mocy:
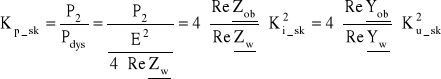
gdzie: Zw - impedancja wewnętrzna źródła
P1 - moc czynna pobierana przez wrota wejściowe czwórnika
P2 - moc czynna wydzielana w obciążeniu czwórnika
Pdys - moc czynna dysponowana źródła wymuszeń
Ki - moduł transmitancji prądowej (wzmocnienie mocy)
Zob - impedancja obciążenia
Impedancja falowa czwórnika - impedancja, przy której obciążenie wrót wtórnych czwórnika o wtórnej impedancji falowej Zf2 powoduje, że impedancja wejściowa pierwotna czwórnika Z1 jest równa jego impedancji falowej pierwotnej Zf1 (analogicznie dla wrót pierwotnych). Stan taki nazywamy dopasowaniem falowym czwórnika po stronie wtórnej. Czwórnik może być obustronnie dopasowany falowo.
Impedancja falowa pierwotna: 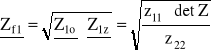
Impedancja falowa wtórna: 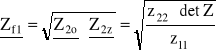
Impedancja falowa: ![]()
Przekładnia falowa: 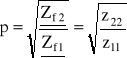
gdzie: Z1o - impedancja pierwotna czwórnika w stanie jałowym
Z1z - impedancja pierwotna czwórnika w stanie zwarcia
z11, z22 - elementy macierzy impedancyjnej
det Z - wyznacznik macierzy impedancyjnej
Dla czwórnika symetrycznego zachodzą związki: Z1 = Z2, Zf1 = Zf2 = Zf, p = 1
Dla czwórnika pracującego w układzie przesyłowym i obustronnie dopasowanego falowo definiujemy tamowność falową: 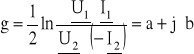
W postaci wykładniczej: 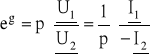
a - tłumienność falowa (wyrażona w neperach) ![]()
b - przesuwność falowa (wyrażona w radianach) b = ½ [(ΨU1 - ΨU2) + (ΨI1 - ΨI2 ± π)]
PRZEKSZTAŁCENIE FOURIERA
Służy do rozłożenia wymuszenia na składowe harmoniczne, których superpozycja przypomina rzeczywiste wymuszenie. Aby do rozkładu sygnału można było wykorzystać szereg Fouriera musi spełniać on warunki Dirichleta:
przebieg musi być bezwzględnie całkowalny w czasie (dla funkcji okresowych: w okresie)
funkcja w przedziale czasu równym okresowi ma skończoną liczbę ekstremów lokalnych
funkcja w przedziale czasu równym okresowi posiada skończoną liczbę punktów nieciągłości, w których przyjmuje wartość średniej arytmetycznej granic prawo- i lewostronnej.
Trygonometryczny szereg Fouriera:
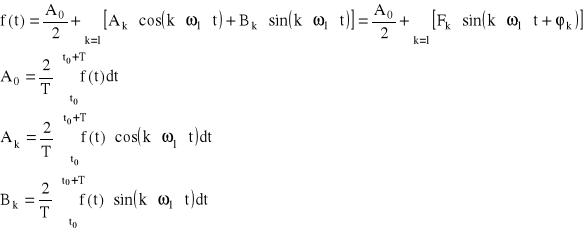
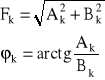
Zespolony szereg Fouriera:
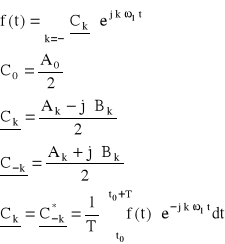
Widmo amplitudowo - częstotliwościowe szeregu zespolonego jest symetryczne względem osi amplitudy, a widmo fazowo - częstotliwościowe jest symetryczne względem początku układu współrzędnych.
Z twierdzenia Parsevala i własności szeregu wykładniczego wynika, że wartość skuteczna sygnału okresowego jest równa: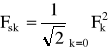
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
Należą do charakterystyk zaciskowych układu. Dzielą się na transmitancje i immitancje.
Immitancje - są to charakterystyki związane z jedną parą zacisków.
Transmitancje - charakterystyki związane z różnymi parami zacisków.
Pasmo przenoszenia - zakres częstotliwości, w których moduł transmitancji przyjmuje wartości nie mniejsze od wartości granicznej: ![]()
, co odpowiada tłumieniu granicznemu w układzie.
Pasmo zaporowe - zakres częstotliwości, w którym moduł transmitancji przyjmuje wartości mniejsze od wartości granicznej.
Selektywność układu - jest to zdolność układu do częstotliwościowego rozdziału sygnałów podawanych na wejście. Miarą selektywności układu jest współczynnik prostokątności zdefiniowany jako iloraz szerokości pasma przenoszenia przy 3 dB, do szerokości pasma przenoszenia przy 20 dB.
Szerokość pasma przenoszenia - Zakres częstotliwości jakie przenosi układ. Ze względu na to dzielimy je na:
- dolnoprzepustowe (0; fg)
- górnoprzepustowe (fg; +∞)
- środkowoprzepustowe
- środkowozaporowe
Częstotliwość graniczna - częstotliwość, dla której moduł transmitancji przyjmuje wartość graniczną.
Częstotliwość środkowa pasma przenoszenia - średnia arytmetyczna częstotliwości granicznych pasma przenoszenia.
Zastępcza dobroć układu - definiowana jako stosunek częstotliwości środkowej pasma przenoszenia do jego szerokości.
Współczynnik nierównomierności charakterystyki amplitudowej
Zniekształcenia amplitudowe
STANY NIEUSTALONE
Stanem nieustalonym nazywamy stan przejściowy pomiędzy dwoma stanami ustalonymi. Podczas jego trwania charakter odpowiedzi jest inny od charakteru wymuszenia.
Sygnał wzorcowy - dowolny sygnał przyczynowy, który umożliwia uwypuklenie na charakterystyce czasowej własności obwodu elektrycznego. Zaliczamy do nich impuls Diraca, sygnał skoku jednostkowego, sygnał liniowo rosnący i inne.
Przebieg - charakterystyka czasowa układu stacjonarnego, liniowego, skupionego (SLS) o danym wyjściu i wejściu.
Charakterystyka skokowa układu - odpowiedź układu na sygnał skoku jednostkowego przy zerowych warunkach początkowych.
Charakterystyka impulsowa układu - odpowiedź na sygnał impulsu Diraca przy zerowych warunkach początkowych.
Komutacja - dowolna zmiana w obwodzie. Zakładamy, że czas trwania komutacji jest zerowy.
I Prawo komutacji - prąd płynący przez cewkę nie może ulec skokowej zmianie, co oznacza, że prąd cewki tuż przed komutacją jest równy prądowi cewki tuż po komutacji.
II Prawo komutacji - napięcie na kondensatorze nie może ulec skokowej zmianie, co oznacza, że napięcie na kondensatorze tuż przed komutacją jest równy napięciu tuż po komutacji.
Stan początkowy układu - to prądy cewek i napięcia kondensatorów tuż przed komutacją.
Składowa wymuszona rozwiązania - to stan ustalony obwodu po komutacji.
Składowa swobodna charakteryzuje procesy zachodzące w układzie na skutek niezerowych warunków początkowych przy braku wymuszeń zewnętrznych i zależy jedynie od warunków początkowych, struktury obwodu i wartości jego elementów.
Stała czasowa obwodu (τ = R·C lub τ = L / R) - czas, po którym odpowiedź stanowi (1 - 1/e) wartości sygnału wymuszenia. Po 3 stałych czasowych odpowiedź stanowi 95% wartości wymuszenia, a po 5 - 99,3%.
Zwis
Iz = U0 / Rw Gw = 1/ Rw
U0 = Iz / Gw Rw = 1/ Gw
Thevenin
Norton
Wyszukiwarka
Podobne podstrony:
WCY Teoria do cw 6, semestr 2, podstawy elektroniki i elektroniki
matrialy, PWR [w9], W9, 5 semestr, Podstawy elektrotechniki Lab, MATERIAŁY, podst ele lab - swistak,
spr 23 moje, Szkoła, Semestr 4, Podstawy elektroniki
aaaasas, Szkoła, Semestr 4, Podstawy elektroniki, Bart
elektronika ćw 4- tyrystor i trika, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektron
wzmacniacz operacyjny, Materiały, II Semestr, Podstawy elektroniki
sprawozdanie na elektre 1, Automatyka i robotyka air pwr, II SEMESTR, Podstawy elektroniki
T5PEL, Automatyka i robotyka air pwr, II SEMESTR, Podstawy elektroniki
sprawko ćw2, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektroniki LAB, Podstawy Elekt
Elektrotechnika 1 kolokwium, Politechnika Wrocławska Energetyka, 3 semestr, Podstawy elektrotechniki
T4PEL, Automatyka i robotyka air pwr, II SEMESTR, Podstawy elektroniki
kolo elektronika, Automatyka i robotyka air pwr, II SEMESTR, Podstawy elektroniki
zestaw 3, semestr 2, podstawy elektroniki i elektroniki
strona tytulowa elektronika, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektroniki LAB
Elektrotechnika egzamin pytania+ odpowiedzi, Mechatronika pollub, semestr I, Podstawy Elektrotechnik
iwanejko 1termin, semestr 2, podstawy elektroniki i elektroniki
zestaw1, semestr 2, podstawy elektroniki i elektroniki
Sprawozdanie nr I, PWR [w9], W9, 5 semestr, Podstawy elektrotechniki Lab, MATERIAŁY, podst ele lab -
ćw 26 - sprawko moje, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektroniki LAB, Podst
więcej podobnych podstron