Mechanika Techniczna
Studia Dzienne
Semestr III
Zadania do ćwiczeń w roku akadem. 2003/04
Ćwiczenie 1 (wykład: 1 i 2)
Zadanie 1
Wyznaczyć równanie toru punktu, jeśli: x=hcos2ωt, y=hcosωt. h[m], ω[1/s]- stałe, t[s]-czas.
Zadanie 2
Z danych równań ruchu punktu wyprowadzić równanie toru i narysować go oraz wyznaczyć równanie ruchu punktu po torze (równanie drogi), licząc drogę od początku położenia punktu. Równania: x=(1/2)t2, y=(1/3)t3.
Zadanie 3
Prędkość lądowania samolotu wynosi v0= 144[km/h]. Obliczyć jego opóźnienie a w [m/s2] przy zatrzymywaniu się oraz czas t1 w [s], jaki upłynie od początku lądowania do zatrzymania się, jeżeli jego droga lądowania jest równa s1= 200[m]. Zakładamy, że opóźnienie jest stałe.
Zadanie 4
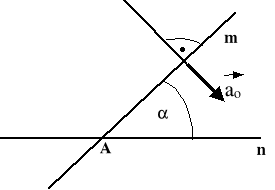
Prosta m porusza się prostopadle do swego kierunku ze stałym przyspieszeniem a0, przy czym jej prędkość w chwili początkowej wynosiła v0. Prosta ta przecina się z nieruchomą prostą n pod stałym kątem ၡ. Wyznaczyć prędkość i przyspieszenie punktu A przecięcia się prostych.
Zadanie 5
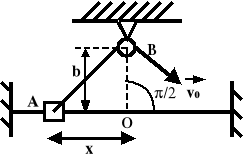
Tulejka A jest przesuwana po pręcie za pomocą linki przerzuconej przez mały krążek B odległy od pręta o wielkość OB=b. Wyznaczyć wzór na prędkość i przyspieszenie tulejki w funkcji odległości OA = x, jeśli swobodny koniec linki jest ciągnięty ze stałą prędkością v0.
Zadanie 6
Ruch punktu określony jest równaniem x(v)=bv2-c. Po jakim czasie prędkość punktu będzie dwa razy większa od prędkości początkowej. W chwili początkowej punkt znajdował się w położeniu x=0.
Zadanie 7
Pociąg mający prędkość początkową vo=54[km/h], przejechał s1=600[m] w ciągu t1=30[s]. Zakładając stałe przyspieszenie styczne pociągu, obliczyć jego prędkość i przyspieszenie całkowite w końcu trzydziestej sekundy, jeżeli ruch odbywał się po łuku o promieniu R=1[km].
Zadanie 8
Punkt A porusza się po krzywej płaskiej zgodnie z równaniem s=b(ekt-1) gdzie s w [m], b, k są stałymi Kąt między całkowitym przyspieszeniem a prędkością wynosi = 60o. Obliczyć prędkość i całkowite przyspieszenie punktu.
Zadanie 9
Dwa punkty A i B poruszają się po okręgu o promieniu R=6 [m] w przeciwne strony zgodnie z równaniami drogi sA(t)=ၰt2 i sB(t)=ၰt4, gdzie sA i sB w [m], t - czas w [s]. Punkty wyruszyły z przeciwnych końców średnicy. Obliczyć normalne i styczne przyspieszenia punktów w momencie ich spotkania.
Zadanie 10
Punkt porusza się po okręgu o promieniu r=2[m] według równania s=0.1თt2, (t - w sekundach, s - w metrach). Po jakim czasie przyspieszenie normalne i styczne będą równe?
Ćwiczenie 2 (wykład: 3 i 4)
Zadanie 1
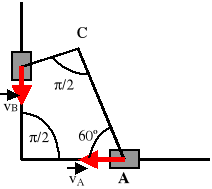
Dla układu przegubowo połączonych prętów jak na rysunku określić prędkość punktu C, jeżeli prędkość punktu A wynosi 8 [m/s] a prędkość punktu B wynosi 6[m/s].
Zadanie 2
Koło mające nieruchomą oś otrzymało początkową prędkość kątową ωo = 2π[rad/s]. Po wykonaniu 10 obrotów, wskutek tarcia w łożyskach, koło zatrzymało się. Obliczyć opóźnienie kątowe ε tego koła uważając je za stałe.
Zadanie 3
Tarcza kołowa obraca się dokoła nieruchomej osi z opóźnieniem kątowym ၨ a początkowa prędkość kątowa tarczy wynosiła . Znaleźć równanie ruchu tarczy (t).
Zadanie 4
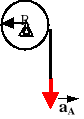
Na bęben o promieniu R=0,5[m] nawinięto linę. Koniec liny A porusza się ze stałym przyspieszeniem. Po przebyciu drogi s = 1/3 [m] koniec A osiągnął prędkość v=1[m/s]. Znaleźć przyspieszenie dowolnego punktu leżącego na obwodzie bębna.
Zadanie 5
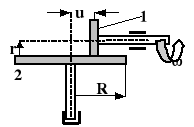
Koło 1 przekładni ciernej wykonuje f1=600[obr/min] i jednocześnie przesuwa się osiowo według równania u=(10-0,5თt), gdzie: u[cm], t[s]. Obliczyć: a) przyspieszenie kątowe ε2 koła 2. w funkcji przesunięcia u, tzn. ε2= ε2(u); b) całkowite przyspieszenie dowolnego punktu B na obwodzie koła 2 w chwili gdy u=r. Przyjąć r=5[cm], R=15[cm].
Zadanie 6
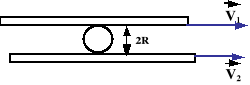
Pomiędzy dwie równoległe odległe od siebie o 2R listwy wstawiono koło, które toczy się względem nich bez poślizgu. Wyznaczyć prędkość środka koła i jego prędkość kątową, jeżeli listwy poruszają się poziomo z prędkościami v1 i v2.
Zadanie 7
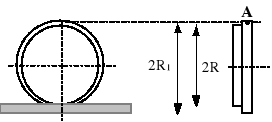
Koło zestawu kołowego toczy się bez poślizgu po prostej szynie ze stała prędkością v. Znaleźć prędkość i przyspieszenie punktu A na obrzeżu koła.
Zadanie 8.
Obliczyć prędkość punktu B mechanizmu oraz prędkości kątowe prętów AB i BD w położeniu jak na rysunku. Korba OA obraca się z prędkością kątową ၷ1 . Zaznaczone na rysunku wymiary prętów wynoszą:
![]()
Ćwiczenie 3(wykład: 5 i 6).
Zadanie 1
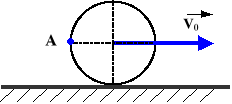
Koło toczy się bez poślizgu po prostej. Obliczyć przyspieszenie punktu A koła w chwili t=2[s], jeśli: vo=12თt[m/s], r=0.2[m].
Zadanie 2
Koło zębate o promieniu R jest uruchamiane korbą OA obracającą się dokoła osi O stałego koła zębatego o tym samym promieniu. Korba obraca się z prędkością kątową stałą ၷo. Wyznaczyć przyspieszenie punktu koła ruchomego, który w danej chwili jest chwilowym środkiem obrotu. Po wyprowadzeniu wzoru ogólnego wykonać obliczenia dla: R = 12 [cm], ၷo = 2 [rad/s].
Zadanie 3
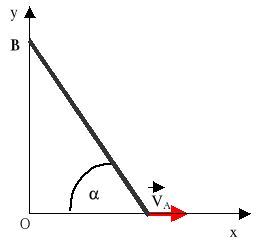
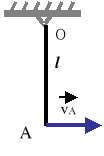
Pręt prosty AB ślizga się ruchem płaskim po osiach układu Oxy. W chwili gdy tworzy on z osią Ox kąt ၡ=60o, prędkość jego końca A wynosi vA= 2[m/s]. Wyznacz dla tego położenia chwilowy środek obrotu, prędkość kątową pręta i prędkość końca B.
Zadanie 4
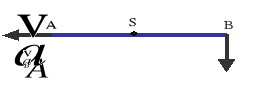
Przyspieszenia końców pewnego pręta prostego wynoszą aA i aB. Wyznaczyć przyspieszenie aS środka S tego pręta, oznaczyć na rysunku jego kierunek i zwrot oraz obliczyć wartość przyspieszenia aS, jeśli aA=aB=21/2 [m/s2].
Zadanie 5
Na szpulę o promieniach a i b nawinięto linę, której koniec A ma prędkość u = const. Obliczyć, jaką drogę sA przebędzie koniec A liny, gdy odcinek AB = e tej liny nawinie się na szpulę. Dane: a, b, e, u.
Zadanie 6
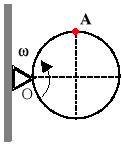
Koło o promieniu R=0,2 [m] obraca się w swej płaszczyźnie wokół stałego punktu O ze stałą prędkością kątową ၷ= 5[rad/s]. Po obwodzie koła przesuwa się punkt ze stałą prędkością vw=1[m/s]. Obliczyć bezwzględne przyspieszenie punktu w położeniu A.
Zadanie 7
Linia kolejowa przebiega wzdłuż południka. Lokomotywa jedzie z prędkością v=180 km/h na południe. Obliczyć przyspieszenie Coriolisa lokomotywy w chwili, gdy jej położenie jest określone szerokością geograficzną północną ၡ=60o.
Zadanie 8
Koło o promieniu R obraca się w swej płaszczyźnie ze stałą prędkością kątową ၷ wokół osi przechodzącej przez jego środek. Po średnicy koła porusza się punkt zgodnie z równaniem drogi s(t)=Rsin(ၷt). Punkt wyruszył ze środka koła. Znaleźć prędkość bezwzględną i przyspieszenie bezwzględne punktu w zależności od czasu.
Ćwiczenie 4 (wykład:7 i 8).
Zadanie 1
Punkt materialny o masie m=0,1[kg] porusza się pod działaniem sił: Fx = -2sin3t [N], Fy = -2cos3t [N]. Określić tor tego punktu przy zerowych warunkach początkowych.
Zadanie 2
Punkt materialny o masie m=2[kg] porusza się zgodnie z równaniami x(t)=hcos(ၷt), y(t)=hsin(ၷt). Wyznacz: a) prędkość w chwili t1=ၰ/ၷ, b) przyspieszenie w chwili t2=2ၰ/ၷ, c) siłę działającą na ten punkt w chwili t2. Przyjąć do obliczeń: h=0,05 [m], ၷ=10[rad/s].
Zadanie 3
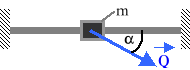
Suwak obrabiarki o masie m=0.6[kg] będąc w stanie spoczynku, został wprawiony w ruch wzdłuż prowadnicy za pomocą siły Q=10[N], skierowanej do osi prowadnicy pod kątem ၡ=30o. Jaką prędkość uzyska suwak po przesunięciu go na odległość s=1[m], jeżeli współczynnik tarcia suwak-prowadnica wynosi µ=0.2?
Zadanie 4
Pocisk o masie m wystrzelono pionowo w górę z prędkością początkową vo. Wiedząc, że siła oporu powietrza jest w postaci R=kთv
(k - stały współczynnik, v - prędkość pocisku), wyznaczyć czas, po którym pocisk osiągnie maksymalną wysokość.
Zadanie 5
Dla układu dwóch mas M i m połączonych nierozciągliwą i lekką nicią wyznaczyć ich przyspieszenie oraz naciąg nici. Ciało o masie M spoczywa na chropowatej równi pochyłej o kącie nachylenia ၡ, współczynnik tarcia o równię wynosi µ. Jaki warunek musi spełniać masa M, aby jej ruch w dół równi był możliwy?
Zadanie 6
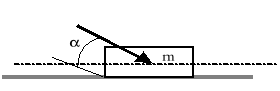
Do ciała o masie m, które może poruszać się prostoliniowym ruchem postępowym po chropowatej poziomej płaszczyźnie, przyłożona została siła P tworząca kąt ၡ z tą płaszczyzną. Wyznaczyć przyspieszenie, z którym zacznie poruszać się to ciało. Po jakim czasie uzyska ono prędkość v1, jeśli na początku miało prędkość vo? Współczynnik tarcia między ciałem a płaszczyzną jest równy µ.
Zadanie 7
Kulka o masie m stacza się po rynnie kołowej o promieniu r bez prędkości początkowej z punktu A. Znaleźć reakcję rynny, gdy kulka będzie mijała punkt B.
Zadanie 8
Z jakim przyśpieszeniem musi poruszać się klin dolny, aby klin górny nie zsuwał się względem dolnego? Między powierzchniami styku klinów nie występuje tarcie, kąt pochylenia klina dolnego wynosi ၡ.
Zadanie 9
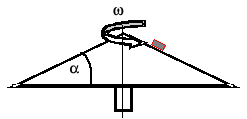
Na powierzchni ruchomego stożka o kącie pochylenia ၡ do poziomu obracającego się ze stałą prędkością kątową ၷ znajduje się punkt materialny o masie m. W jakiej największej odległości r od osi obrotu może pozostawać ten punkt aby nie nastąpił jego poślizg po tworzącej stożka. Współczynnik tarcia statycznego wynosi µ.
Zadanie 10
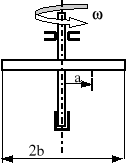
Pozioma gładka rurka o długości 2b jest osadzona symetrycznie na pionowej osi obracającej się ze stałą prędkością kątową ၷ. Wewnątrz rurki znajduje się kulka o masie m. W początkowej chwili kulka znajdowała się w spoczynku w odległości a od osi obrotu. Wyznaczyć poziomą reakcję rurki na kulkę w chwili, w której ta opuści rurkę.
Ćwiczenie 5 (wykład: 9)
Zadanie 1
Lufa działa jest nachylona poziomo a działo ma ciężar G=11[kN]. Ciężar pocisku wynosi P=5,5[N]. Prędkość pocisku u wylotu lufy wynosi v=900[m/s]. O ile i w którą stronę przesunie się działo, jeżeli opory jego ruchu są równe 0,1G ?
Zadanie 2
Pocisk artyleryjski o masie m=30[kg] wylatuje z lufy armaty z prędkością v=50[m/s]. Jaka jest siła odrzutu działająca na armatę, jeśli lot pocisku w lufie trwał 0,1[s].
Zadanie 3
Dwie kule, jedna o masie m1=200[g], a druga o masie m2=300[g] poruszają się do siebie wzdłuż prostej z prędkościami odpowiednio v1=0.5[m/s] i v2=0.4[m/s] W pewnej chwili zderzyły się i następnie zaczęły poruszać się razem. Znaleźć ich wspólną prędkość oraz kierunek ruchu.
Zadanie 4
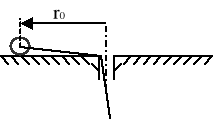
Punkt o masie m jest zamocowany do nieważkiej i nierozciągliwej nici i porusza się po okręgu o promieniu ro ze stałą prędkością kątową ωo. Następnie nić została wciągnięta do otworu i punkt porusza się po okręgu o promieniu 0.5ro. Pomijając opory ruchu, obliczyć, w jakim stopniu zmieni się naciąg nici.
Zadanie 5
Samochód jedzie z prędkością vo=108[km/h] w dół po stoku nachylonym do poziomu pod kątem ၡ=0.008[rad]. W pewnej chwili kierowca zobaczywszy niebezpieczeństwo zaczyna hamować. Opór całkowity hamowania jest stały i wynosi 0.1 ciężaru samochodu. Obliczyć, w jakiej odległości d i po jakim czasie ၴ samochód zatrzyma się. Przyjąć sinၡ Ⴛ ၡ.
Zadanie 6
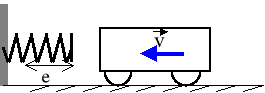
Wagonik o masie m=103[kg] jedzie z prędkością v=36[km/h] po torze prostym poziomym i uderza o zderzak. Jaka musi być sztywność sprężyny zderzaka aby jego ugięcie e=0.5[m]? Zakładamy liniową charakterystykę sprężyny i brak strat energii mechanicznej.
Zadanie 7
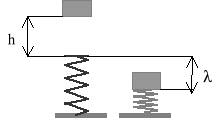
Ciężarek o masie m startując ze stanu spoczynku spada pionowo z wysokości h na nieważką sprężynę śrubową o stałej sztywności równej k. Wyznacz ugięcie ၬ tej sprężyny zakładając, że ciężarek po zetknięciu z górnym końcem sprężyny przykleił się do niej. Opory ruchu pomijamy.
Zadanie 8
Mała kula o masie M = 1[kg] wykonuje ruch harmoniczny u(t) = 12თsin2t (gdzie: u - w metrach, t - w sekundach). Obliczyć energię mechaniczną kuli, jeśli sztywność sprężyny, na której jest oparta kula k = 4[N/m].
Zadanie 9
Z wysokości h=10[m] spada klocek o masie m=5[kg]. Ile procent energii kinetycznej zostało przez ten klocek stracone w wyniku oporu powietrza, jeśli przy zetknięciu z Ziemią prędkość klocka była równa v=10[m/s].
Zadanie 10
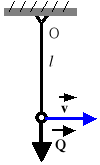
Kula o ciężarze Q=2[kG] zawieszona na nieważkiej lince o długości l=1[m] uzyskała wskutek uderzenia prędkość v=5[m/s]. Oblicz siłę w lince bezpośrednio po uderzeniu. Podaj wynik obliczenia z dokładnością do 0.01[N].
Ćwiczenie 6 (wykład: 10 i 11)
Zadanie 1
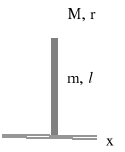
Obliczyć moment bezwładności drążka zmiany biegów samochodu względem jego osi x. Zakładamy, że drążek składa się z jednorodnego pręta o masie m i długości l z osadzoną na nim kulką o promieniu r i masie M.
Zadanie 2
Obliczyć moment bezwładności stanowiska pracy względem płaszczyzny podłogi. Składa się ono z blatu będącego kwadratową płytą o wymiarach 2x2 m i masie 12 [kg] oraz czterech jednakowych prostopadłościennych wsporników o wymiarach 0,03x0,03x1,2 m i masie
3 [kg] każdy.
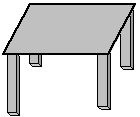
Zadanie 3
Znaleźć momenty bezwładności i dewiacji układu 3 jednorodnych prętów każdy o masie m i długości l połączonych tak jak na rysunku.
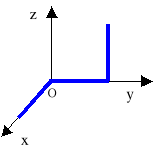
Zadanie 4
Obliczyć przesunięcie pływającego żurawia, przenoszącego ciężar P1=2[T], jeśli wysięgnik z pozycji pionowej obróci się o kąt ၡ=30o. Ciężar żurawia P2=20[T]. Długość wysięgnika OA = l = 8[m]. Opór wody i ciężar wysięgnika pominąć.
Zadanie 5
Oblicz energię kinetyczną układu składającego się z jednorodnej belki o masie M i dwóch jednakowych rolek o masie m i promieniu r. Belka jest przetaczana po rolkach ze stałą prędkością v.
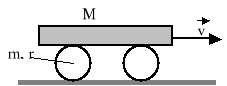
Zadanie 6
Jednorodny walec o masie m i promieniu r wiruje wokół swej nieruchomej osi symetrii z prędkością kątową ၷ0. Oblicz energię kinetyczną i kręt tego walca.
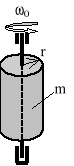
Zadanie 7
Ile wynosi energia kinetyczna i kręt płyty kwadratowej o boku a i masie m wirującej z prędkością kątową ωo=const wokół swego nieruchomego boku?
Zadanie 8
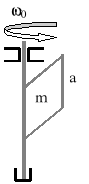
Prosty jednorodny pręt o długości l=3,27 [m] osadzony jest swoim końcem O obrotowo na osi i może wykonywać ruchy w płaszczyźnie pionowej, prostopadłej do tej osi. Jaką prędkość trzeba nadać końcowi A, aby pręt z położenia równowagi wykonał pół obrotu?
Zadanie 9
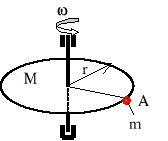
Jednorodna tarcza kołowa o masie M i promieniu r obraca się ze stałą prędkością kątową ၷ wokół własnej pionowej i nieruchomej osi symetrii, przy czym na obwodzie tarczy spoczywa punkt A o masie m. Co stanie się, jeśli po przesunięciu punkt A znajdzie się w środku tarczy? Opory ruchu pomijamy.
Zadanie 10
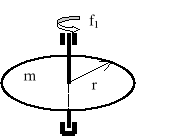
Jednorodna tarcza kołowa o promieniu r=0,3[m] i masie m=2[kg] jest wykonana z tworzywa nasączonego równomiernie cieczą. Tarcza obracała się na początku wokół własnej osi symetrii ze stałą częstotliwością f1=10/ၰ [Hz]. Oblicz, jaką prędkość kątową ၷ2 [rad/s] osiągnęła tarcza, jeśli po osuszeniu jej masa zmniejszyła się o 20%. Opory ruchu pomijamy.
Zadanie 11
Dwie wirujące na jednej nieważkiej osi tarcze z prędkościami kątowymi ၷ1 i ၷ2 zostały nagle połączone. Jak zmieni się energia kinetyczna i kręt układu, i momenty bezwładności tych tarcz względem osi obrotu wynosiły odpowiednio J1 i J2?
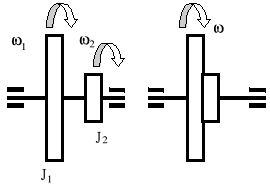
Ćwiczenie 7 (wykład: 12 i 13)
Zadanie 1
Oblicz reakcje dynamiczne w łożyskach A i B dwuramiennego śmigła samolotu w czasie jego obrotu, jeśli wskutek złego wykonania oś symetrii śmigła jest odchylona od osi obrotu o kąt ၡ=0,015 [rad], a jego środek leży na osi obrotu. Śmigło należy traktować jako pręt prosty jednorodny. Ciężar śmigła P=147,15[N], jego moment bezwładności względem osi symetrii J=4.905 [kg m2], wymiary: h=0,25[m], a=0,15[m], a prędkość obrotowa jest stała i wynosi n=3000 [obr/min.].
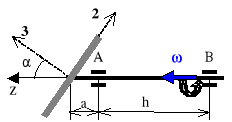
Zadanie 2
Jednorodne koło zamachowe o ciężarze Q=1[T] i promieniu r=0,6[m] jest osadzone na ułożyskowanej osi AB i obraca się z prędkością n=1200[obr/min.]. Geometryczna oś obrotu jest przesunięta równolegle względem osi symetrii koła o wielkość e =1[mm]. Obliczyć reakcje dynamiczne łożysk A i B jeśli h=0,4[m].
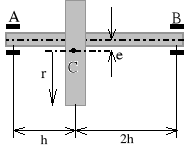
Zadanie 3
Napędowe koło samochodu o promieniu tocznym r i ciężarze P porusza się po prostej poziomej. Do koła jest przyłożony moment obrotowy M. Ramię bezwładności koła względem jego osi centralnej, prostopadłej do jego płaszczyzny, wynosi ၲ. Współczynnik tarcia suwnego wynosi µ. Jaki warunek musi spełniać moment obrotowy, aby koło toczyło się bez poślizgu? Opory toczenia pomijamy.
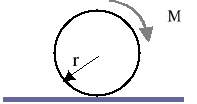
Zadanie 4
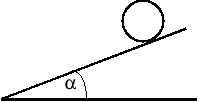
Oblicz, jaki kąt ၡ powinna tworzyć z poziomem płaszczyzna, po której ma się toczyć bez poślizgu walec, jeżeli wiadomo, że współczynnik tarcia między walcem a płaszczyzną wynosi m.
Zadanie 5
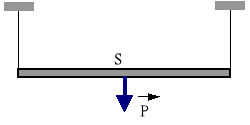
Prosty jednorodny pręt AB o ciężarze P jest zawieszony poziomo na dwóch pionowych linkach przyczepionych do sufitu. Oblicz siłę naciągu jednej linki w chwili zerwania się drugiej.
Zadanie 6
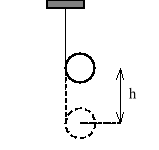
Walec o masie m owinięto linką, której drugi koniec przymocowano do stałego punktu A. W pewnej chwili walec zaczął swobodnie opadać, odwijając swobodnie się z linki. Obliczyć prędkość v osi walca w chwili, gdy jego środek obniżył się o wysokość h oraz obliczyć siłę naciągu linki.
Zadanie 7
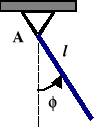
Wyznacz równanie małych drgań swobodnych pręta jednorodnego o długości l=1[m], zamocowanego obrotowo w punkcie A
i wykonującego ruch w płaszczyźnie pionowej. Oblicz okres tych drgań z dokładnością do 0,01[s].
Wyszukiwarka
Podobne podstrony:
pewniaki z rozwiazaniami, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, chomika od barta, M
Mega ściąga z teorii, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, chomika od barta, Mecha
dzial 10 i12 z rozwiazaniem, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, chomika od barta
Mechana III lab, Szkoła, Semestr 4, Mechanika Techniczna III, Ćw. 5
Finanse - zadania, SZKOŁA, semestr II, Podstawy finansów
Tem-egz-sem III 2008, gik, semestr 3, Geodezja wyższa
NS I stop sem III Ekolog, Szkoła
materały pdf sem III Egzamin BM Inż Mat 2007 2008 II
materały pdf sem III, Egzamin BM Inż Mat 2007 2008 II
ZAGADNIENIA NA EGZAMIN Z MECHANIKI TECHNICZNEJ II DLA SEMESTRU III, sem III, +Mechanika Techniczna I
76ytryhtf, Szkoła, Semestr 3, Semestr 3, Mechanika techniczna II, mechanika techniczna II, notatki,
Zadania energetyka, Szkoła, Semestr III, technologia maszyn energetycznych, Materiały Skiepki, Kol 1
Zaliczenie do reki, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR III, Chemia
kolo 1 semestr 3, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR III, Chemia,
więcej podobnych podstron