Państwowa Wyższa Szkoła Zawodowa w Krośnie Instytut Politechniczny |
|||
Laboratorium Mechaniki Płynów |
|||
Prowadzący: |
Data ćw. |
||
|
Nr indeksu: |
Ocena |
Ocena |
|
Specjalność: |
|
|
Protokół z ćwiczenia nr 1
1. Temat ćwiczenia: Opływ walca kołowego.
2. Cel ćwiczenia:
Celem ćwiczenia jest eksperymentalne określenie rozkładu ciśnienia na powierzchni walca kołowego oraz stwierdzenie rodzaju przepływu w danym układzie.
3. Podstawy teoretyczne:
Ciśnienie na powierzchni okręgu utworzonego przez zerową linię prądu ψ = 0 jest opisana zależnością:
pω = p∞ + q∞(1- 4 sin2 ϑ)
gdzie:
pω - ciśnienie statyczne przepływu niezakłóconego,
q∞ = ![]()
- ciśnienie dynamiczne przepływu niezakłóconego,
U∞ - prędkość przepływu niezakłóconego,
ρ - gęstość medium.
Związek ten może być przekształcony do postaci opisującej tzw. współczynnik ciśnienia definiowany jako
![]()
=![]()
=1-4sin2ϑ.
Na element powierzchni walca o jednostkowej długości działa elementarna siła powierzchniowa
dP = pω l R d ϑ
co po zsumowaniu sił działających na cały obwód walca i po rozłożeniu na kierunki x i y daje
Px = - R![]()
pω cos ϑ dϑ
Py = - R![]()
pω cos ϑ dϑ
Jeżeli w miejsce pω podstawiona zostanie zależność pω = p∞ +q∞ (1 - 4 sin2 ϑ), wówczas po scałkowaniu otrzymamy:
Px = 0 (siła oporu)
Py = 0 (siła nośna)
Oznacza to, że na walec opływany płynem idealnym nie działa żadna siła (paradoks d' Alamberta). Wynik ten jest sprzeczny z doświadczeniem, co oznacza, że lepkość zmieniać musi obraz opływu, przy czym mechanizm tego oddziaływania jest dwojaki:
lepkość prowadzi do ukształtowania takiego rozkładu ciśnień na powierzchni opływanego ciała, który daje różną od zera siłę wypadkową (siła opory ciśnieniowego Pxc),
lepkość powoduje występowanie na powierzchni opływanego ciała sił stycznych dających niezerową wypadkową (opór tarcia Pxt).
Suma oporu ciśnienia i tarcia przy założeniu, że kierunek przepływu pokrywa się z osią x, może być opisana zależnością
Px = Pxc + Pxt = ![]()
p cos(![]()
)dS + ![]()
τ cos(![]()
) ds.
Dwa szeregi wirów są przesunięte względem siebie o ![]()
l, a odległość poszczególnych szeregów wynosi ![]()
= 0,28 l; układ ten jest znany powszechnie jako ścieżka wirowa Karmana. Jak wykazały liczne doświadczenia, wyraźny obraz ścieżki wirowej zaobserwować można jedynie wówczas, gdy warstwa przyścienna na powierzchni opływanego walca ma charakter laminarny. Przepływ taki jest nazywany powszechnie podkrytycznym, punkt maksymalnej depresji występuje wówczas przy α ≈ 70o, podczas gdy oderwanie zauważa się dla α ≈ 85o. W przypadku, gdy prędkość płynu opływającego walec jest na tyle duża, że na jego powierzchni występuje przejście warstwy przyściennej laminarnej w turbulentną (przed punktem oderwania), wówczas punkt 0 przesuwa się w stronę tylnej powierzchni walca (α = 140o) i opływ taki jest nazywany nadkrytycznym.
Obszar cienia aerodynamicznego za opływanym ciałem jest wówczas znacznie węższy, w porównaniu z przepływem podkrytycznym, czego rezultatem jest wyraźny spadek współczynnika oporu.
4. Opis i schemat stanowiska
Najważniejsze elementy tunelu aerodynamicznego, w którym jest realizowany pomiar, pokazano schematycznie na rysunku (1). Wentylator zasysa powietrze z otoczenia do komory pomiarowej 1, a odpowiednio kształtowana dysza wlotowa 2 zapewnia uzyskanie jednorodnego profilu prędkości. W połowie wysokości komory zamontowany jest walec 3 w uchwycie 4 zapewniającym jego obrót w zakresie od 0o do 360o. Kątomierz 5 obracający się wraz z walcem umożliwi odczyt kąta α utworzonego między osią otworu pomiarowego 6, a kierunkiem napływającego strumienia. Ciśnienie rejestrowane na powierzchni walca jest przekazywane do mikromanometru 7, którego drugi koniec jest połączony z otworami w ścianie tunelu 8, służącymi do pomiaru ciśnienia statycznego p∞ w komorze pomiarowej.
Rys.1. Schemat stanowiska badawczego.
5. Wyniki pomiarów i obliczeń
![]()
n |
ၡၮ |
cosn |
ln [m] |
၄ၰၷၮ ၭု၎ၛဲၝ |
|
၄ၰၷၮၳၯၣၡၮ ၭု၎ၛဲၝ |
1 |
0 |
1 |
0,086 |
348,85 |
1,0000 |
348,85 |
2 |
10 |
0,9848 |
0,084 |
340,74 |
0,9767 |
335,56 |
3 |
20 |
0,9397 |
0,081 |
328,57 |
0,9419 |
308,76 |
4 |
30 |
0,866 |
0,079 |
320,46 |
0,9186 |
277,52 |
5 |
40 |
0,766 |
0,076 |
308,29 |
0,8837 |
236,15 |
6 |
50 |
0,6428 |
0,074 |
300,18 |
0,8605 |
192,95 |
7 |
60 |
0,5 |
0,072 |
292,06 |
0,8372 |
146,03 |
8 |
70 |
0,342 |
0,071 |
288,01 |
0,8256 |
98,50 |
9 |
80 |
0,1736 |
0,071 |
288,01 |
0,8256 |
50,00 |
10 |
90 |
0 |
0,069 |
279,89 |
0,8023 |
0,00 |
11 |
100 |
-0,1736 |
0,066 |
267,72 |
0,7674 |
-46,48 |
12 |
110 |
-0,342 |
0,058 |
235,27 |
0,6744 |
-80,46 |
13 |
120 |
-0,5 |
0,041 |
166,31 |
0,4767 |
-83,16 |
14 |
130 |
-0,6428 |
0,004 |
16,23 |
0,0465 |
-10,43 |
15 |
140 |
-0,766 |
-0,038 |
-154,14 |
-0,4419 |
118,07 |
16 |
150 |
-0,866 |
-0,076 |
-308,29 |
-0,8837 |
266,98 |
17 |
160 |
-0,9397 |
-0,108 |
-438,09 |
-1,2558 |
411,68 |
18 |
170 |
-0,9848 |
-0,119 |
-482,72 |
-1,3837 |
475,38 |
19 |
180 |
-1 |
-0,104 |
-421,87 |
-1,2093 |
421,87 |
20 |
190 |
-0,9848 |
-0,067 |
-271,78 |
-0,7791 |
267,65 |
21 |
200 |
-0,9387 |
-0,029 |
-117,64 |
-0,3372 |
110,43 |
22 |
210 |
-0,866 |
0,023 |
93,30 |
0,2674 |
-80,80 |
23 |
220 |
-0,766 |
0,057 |
231,22 |
0,6628 |
-177,11 |
24 |
230 |
-0,6428 |
0,068 |
275,84 |
0,7907 |
-177,31 |
25 |
240 |
-0,5 |
0,072 |
292,06 |
0,8372 |
-146,03 |
26 |
250 |
-0,342 |
0,072 |
292,06 |
0,8372 |
-99,89 |
27 |
260 |
-0,1736 |
0,072 |
292,06 |
0,8372 |
-50,70 |
28 |
270 |
0 |
0,073 |
296,12 |
0,8488 |
0,00 |
29 |
280 |
0,1736 |
0,073 |
296,12 |
0,8488 |
51,41 |
30 |
290 |
0,342 |
0,075 |
304,23 |
0,8721 |
104,05 |
31 |
300 |
0,5 |
0,077 |
312,35 |
0,8953 |
156,17 |
32 |
310 |
0,6428 |
0,078 |
316,40 |
0,9070 |
203,38 |
33 |
320 |
0,766 |
0,08 |
324,51 |
0,9302 |
248,58 |
34 |
330 |
0,866 |
0,081 |
328,57 |
0,9419 |
284,54 |
35 |
340 |
0,9397 |
0,084 |
340,74 |
0,9767 |
320,19 |
36 |
350 |
0,9848 |
0,087 |
352,91 |
1,0116 |
347,55 |
Obliczenia:
![]()
T = 21[° C] ⇒ 294 [K] - temperatura powietrza,
Lw = 250 [mm] - długość walca,
d = 10 [mm] ⇒ 0,01 [m] - średnica walca,
β = 30°,
i = sin β = ![]()
,
ρm = 827 ![]()
- gęstość cieczy manometrycznej,
obliczamy gęstość powietrza ρp ze wzoru: ρp = ![]()
⇒ ![]()
= 1,16 ![]()
,
obliczamy nadciśnienie na powierzchni walca Δpωn ze wzoru : dla pierwszego pomiaru Δpωn = ρ ·g· ln· i
Δpω1 = 827 ·9,81 ·0,086 ·![]()
= 348,85![]()
tak samo obliczamy dla kolejnych odczytów zmieniając wartości ln,
ciśnienie dynamiczne przepływu niezakłóconego q∞ = Δpω α=0 = 348,85 ![]()
= const.
![]()
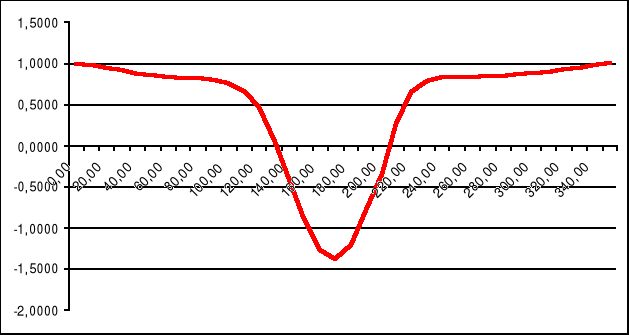
Wykres f(ၡ) =
![]()
Re =
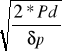
V =
V= 24,52491379
Re = (24,52491379 * 0,01)/(17,4 * 10-6 * (294/273)3/4) = 13332,74
Re k1 = 2300 Re k2 = 50 000
Re k1 < Re < Re k2
Pxc jedn.= suma ၄ၰၷၮၳၯၣၡၮ ၭု၎ၛဲၝ ·Δၡ [rad]·R[m]=4,21486712
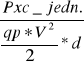
Cx = = 1, 2082;
6. Wnioski
Przy niskich wartościach liczby Reynoldsa w przepływie dominują siły lepkości (duża wartość μ). Przy wysokich wartościach liczby Reynoldsa - siły bezwładności poruszającego się płynu (duża wartość iloczynu ςvl, a mała μ). W naszym przypadku nie da się jednoznacznie powiedzieć czy przepływ jest laminarny czy turbulentny.
Na wykresie można zaobserwować że linia odcięcia przypada na wartość α = 137º, co jest bliskie przepływowi nadkrytycznemu i może sugerować że warstwa przyścienna jest turbulentna.
Pomiary wykonane zostały za pomocą mikromanometru, którego jeden koniec jest połączony z otworami w tunelu, co pozwoliło nam, na odczytanie ciśnienia rejestrowanego na powierzchni walca. Błąd jaki mógł wystąpić, to błąd odczytu wartości ln, odczytywanego przez obserwatora na mikromanometrze.
![]()
![]()
![]()
![]()
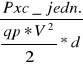
Wyszukiwarka
Podobne podstrony:
223 403587380
222 i 223, Uczelnia, Administracja publiczna, Jan Boć 'Administracja publiczna'
arkusz WOS poziom r rok 2007 223
223 B8 4 A W04 zestawienie slus Nieznany
223 B8 4 A W09 wykaz drobnych e Nieznany
223 Manuskrypt przetrwania
07 223 1655 PRAWO ZAMÓWIEŃ PUBLICZNYCH
metodologia 218 223
!223 Elementy Cewkiid 502 Nieznany (2)
GW 223 GW 07 prezentacja
Anastasi, Urbina, Testy Psychologiczne,18 27, 122 223, 448 492(1)
MAKIJAŻ 223 AISHWARYA RAI
NORCOM Dz U 2004 223 2261 rozp opłaty w SKP 2009 10 07
213 223
credit card visa hack ucam cl tr 560 [223 kb www netz ru] www!osiolek!com ACAXYQUJ6LJYAEVJKHBMLT2XNT
223
223
kk, ART 223 KK, 2001
więcej podobnych podstron