Cel ćwiczenia:

Zbadanie rozkładu obrazu interferencyjnego dzięki klasycznemu doświadczeniu Younga. Obliczenie odległości między szczelinami.

Przebieg ćwiczenia:

Na ekranie umieszczamy kartkę papieru milimetrowego, a w uchwycie slajd z dwiema szczelinami znajdującymi się w odległości d od siebie, upewniając się, że wiązka lasera trafia dokładnie w szczelinki. Następnie z wielka starannością oznaczamy na papierze milimetrowym położenia maksimów interferencyjnych. Pomiary powtarzamy dla dwóch pozostałych par szczelin.

Pomiary:

Pomiar 1

17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
85,5	80,5	76	71,5	66	61	56	51	46,5	41	36,5	31,5	25,5	20	15,5	10,5	5	0

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
0	5	10,5	16,5	20,5	25,5	31,5	37	41	47	51,5	56	61	66,5	72,5	76,5	81,5	87

Pomiar 2

14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
65,5	60,5	55,5	51,5	46,5	41,5	37,5	33,5	28,5	24,5	19,5	14,5	9,5	5	0

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
0	5,5	11	16	21	25,5	30,5	35,5	40,5	45	50	55,5	60,5	64,5	70,5

Pomiar 3

17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
41,5	39,5	37,5	34,5	32	29,5	27,5	25,5	23	20	17,5	14,5	12,5	10,5	8	5,5	2,5	0

0	1	2	3	4	5	6	7	8	9	0	11	12	13	14	15	16	17
0	3	5	7,5	10,5	12,5	14,5	16,5	19	21,5	23,5	26	28,5	31	33,5	35,5	38	40

Obliczenia:

L = 2 m

∆L = 0,001 m

λ = 635 nm = 635·10^-9 m

Pomiar 1

n	xn
0	0
1	5
2	10,5
3	16
4	20,25
5	25,5
6	31,5
7	36,75
8	41
9	46,75
10	51,25
11	56
12	61
13	66,25
14	72
15	76,25
16	81
17	86,25

A = (5.06±0.02) mm

Pomiar 2

n	xn
0	0
1	5,25
2	10,25
3	15,25
4	20,25
5	25
6	29,5
7	34,5
8	39
9	43,25
10	48,25
11	53,5
12	58
13	62,5
14	68

A = (4.79±0.02) mm

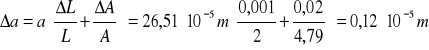
Pomiar 3

n	xn
0	0
1	2,75
2	5,25
3	7,75
4	10,5
5	12,5
6	14,5
7	17
8	19,5
9	22,25
10	24,5
11	26,75
12	29
13	31,5
14	34
15	36,5
16	38,75
17	40,75

A = (2.39±0.01) mm

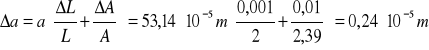
Wnioski:

W trakcie przeprowadzania doświadczenia ręcznie zaznaczaliśmy położenie maksimów na papierze milimetrowym, więc liczymy się z relatywnie dużą niedokładnością pomiarów.

Obrazy uzyskane w doświadczeniu możemy porównać z wariantem c na rysunku 2 w instrukcji, który przedstawia fizyczną sytuację jednoczesnej dyfrakcji i interferencji na dwóch szczelinach.

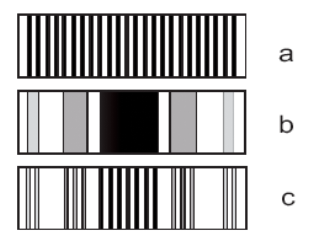
Rysunek 2: a - obraz interferencyjny, b - obraz dyfrakcyjny (jedna szczelina),c - nałożenie obu efektów.

Nałożenie się tych dwóch efektów wynika z tego, że grubość szczelinek jest większa niż długość fali. Fale ugięte na każdej ze szczelin nie oświetlają równomiernie ekranu, dlatego trzeba wziąć pod uwagę dodatkowe efekty dyfrakcyjne, powstające na każdej ze szczelin. Te dodatkowe efekty zmieniają postać funkcji I(α) nadając jej charakter okresowy, przy niezmiennych położeniach kolejnych maksimów i minimów.

---