POLITECHNIKA CZĘSTOCHOWSKA

Katedra Fizyki Ciała Stałego

Laboratorium z Fizyki

Ćwiczenie nr. 3

Wyznaczanie grubości cienkiej folii aluminiowej metodą

pochłaniania promieni β.

Wykonali :

Stefanowski Marcin

Teperski Bartłomiej

Słomka Marek

Częstochowa 1988

1. Część teoretyczna

Natura fizyczna promieniowania

Masa jądra zawierającego określoną liczbę nukleonów, zależy od kombinacji liczby protonów i neutronów zawartych w jądrze. Każde jądro, w którym liczba protonów i neutronów nie odpowiadają kombinacji dających najmniejszą masę jądra podlega przemianom jądrowym w wyniku których jądro osiąga najmniejszą masę. Wyróżniany dwa rodzaje przemian β w jądrze atomu. W przemianie β^- jeden neutron w jądrze przekształca się w jądrze przekształca się proton, a z jądra wysyłany jest wówczas elektron antyneutrino elektronowe (masa spoczynkowa, ładunek , moment magnetyczny neutrino i antyneutrino jest równy zero).

Podczas przemiany β⁺ jeden z protonów wchodzących w skład jądra przekształcony zostaje w neutron, emitowany jest wówczas pozyton i neutrino elektronowe.

Rozpad protonu wchodzącego w skład jądra jest jednak możliwy gdy masa powstałego w wyniku rozpadu jądra jest mniejsza od masy jądra ulegającego rozpadowi o wielkość przewyższającego masę spoczynkową pozytonu. Przekształcenie protonu w neutron może nastąpić na drodze wychwytu elektronu z równoczesnym wysłaniem neutrina elektronowego.

p+e^--> n+v_e

Proton znajdujący się w jądrze może wychwycić jeden z elektronów orbitalnych jeśli tylko suma mas jądra początkowego i elektronu jest większa od masy jądra końcowego. Należy dodać, że trzeba brać pod uwagę nie masę spoczynkową elektronu, lecz masę elektronu w atomie. Masa ta jest mniejsza od masy spoczynkowej o wielkość równoważną energii wiązania elektronu w atomie.

Oddziaływanie promieniowania β z materią

Oddziaływanie promieniowania β z materią ma - przede wszystkim ze względu na małą masę elektronów - nieco odmienny charakter niż oddziaływanie ciężkich cząstek naładowanych. Przy zderzeniach cząstek β z elektronami i jądrami atomów absorbenta w przeciwieństwie do ciężkich cząstek silnie zmienia się ich kierunek ruchu. Cząstki β zderzając się z elektronami mogą znikać, powstają wówczas dwa kwanty promieniowania γ. Zjawisko to nosi nazwę anihilacji. Gdy grubość absorbenta jest mniejsza od zasięgu ciężkich cząstek naładowanych, to praktycznie wszystkie cząstki przez taką warstwę przechodzą. Tory cząstek są liniami łamanymi i łączna długość toru jest większa do odległości między punktem wniknięcia cząstki a punktem jej zatrzymania. Dlatego też nawet przy grubościach absorbenta mniejszej do łącznej długości toru cząstek β, ich część zostaje zatrzymana w absorbencie. Dalsze zwiększanie grubości absorbenta powoduje zatrzymanie coraz większej liczby cząstek.

Cząstki β nie są monoenergetyczne ale mają widmo ciągłe.

Liniowy współczynnik absorbcji

Okazuje się, że dla cząstek o takim widmie wykres przedstawiający zależność ln(I/I₀) od grubości absorbenta x jest linią prostą wynika stąd, że natężenie wiązki cząstek β przez absorbent można przedstawić zależnością:

I₀ - natężenie wiązki cząstek β padających na absorbent,

I - natężenie wiązki cząstek po przejściu przez absorbent,

x - grubość absorbenta,

μ - współczynnik absorbcji.

Masowy współczynnik absorbcji

Masowym współczynnikiem absorpcji nazywamy iloraz współczynnika absorpcji μ i gęstości ρ absorbenta. Jest on w przybliżeniu niezależny od absorbenta i wyraża się wzorem:

Oddziaływanie promieniowania β to jest oddziaływaniem kulomboskim z jądrami bądź z elektronami absorbenta. Oddziaływania te można podzielić na:

a). Jonizacja i wzbudzanie atomów

Proces jonizacji polega na wybijaniu przez padające cząstki podobnie jak w przypadku ciężkich cząstek naładowanych. Proces wzbudzenia zaś polega na przechodzeniu elektronów na dalsze powłoki elektronowe co wiąże się ze wzrostem energii atomu.

b). Zderzenia sprężyste z jądrami i elektronami.

Przy zderzeniach z jądrami cząstki β zmieniają kierunek swego ruchu prawie bez straty energii. Przy zderzeniach z elektronami, oprócz zmiany kierunku cząstki β mogą przekazywać znaczną część energii elektronom.

c). Zderzenia niesprężyste z jądrami.

Proces ten polega na odchylaniu toru padającej cząstki β w polu elektrycznym jądra, będące przyczyną emisji przez nie promieniowania elektromagnetycznego zwanego promieniowaniem hamowania.

Wszystkie wymienione procesy powodują usuwanie cząstek β z padającej wiązki. Udział poszczególnych procesów w absorbcji cząstek zależy od ich energii oraz od liczby masowej absorbenta. Przy małych energiach cząstek β przeważają straty energii na jonizację, przy energiach dużych straty na promieniowanie hamowania.

Gdy absorbentem jest pierwiastek lekki to przeważnie jonizacja, w pierwiastkach ciężkich procesy jonizacji i zderzenia z jądrami odgrywają prawie jednakową rolę.

Detekcja promieniowania jądrowego

Istnieje bardzo wiele metod detekcji promieniowania jądrowego, które umożliwiają określenie rodzaju cząstki, jej pędu, energii, ładunku, masy i innych wielkości.

Licznik Geigera-Mullera należy do grupy detektorów jonizujących. Zasada działania tych detektorów polega na rejestracji prądu jonowego, wytworzonego w przestrzeni detektora.

Licznik G -M ma kształt cylindrycznej rurki metalowej wewnątrz której, wzdłuż jej osi symetrii, jest umieszczony cienki drut wolframowy. Cylindryczna rurka jest napełniona odpowiednią mieszaniną gazów i zamknięta w naczyniu próżniowym. Cylindryczna rura nosi nazwę katody gdyż zawsze pracuje na niższym potencjale względem drutu który jest anodą. Przechodzące przez licznik G-M cząstki powodują wyładowania elektryczne w gazie zawartym w detektorze. Przepływające impulsy prądu między anodą i katodą, zasilaczem i oporem R wytwarzają na oporze R krótkie impulsy napięcia. Impulsy te są doprowadzane na siatkę lampy wzmaczniacza impulsów, wzmocnione i policzone przez układ zliczający.

Komory jonizujące.

Komora jonizująca składa się z dwu elektrod różnego kształtu i rozmiarów, między którymi zostałą wytworzona różnica potencjałów rzędu kilkuset wolt. Najczęściej są stosowane komory jonizacyjne w formie płaskiego kondensatora lub w formie cylindra o przewodzących ściankach na osi którego osadzony jest metalowy pręt odizolowany od ścianek. Szybka cząstka naładowana wytwarza w gazie wypełniającym komorę jony które pod wpływem pola elektrycznego dążą do elektrod, jny dodatnie do katodym ujemne do anody. W rezultacie w obwodzie utworzonym przez przestrzeń między elektrodami, baterię i przewody płynie tzw. prąd jonizacyjny o bardzo małym natężeniu. Z natężenia tego prądu można określić jonizację wytworzoną w objętości komory zawartej między elektrodami.

II. Tabele pomiarów

Załączone na osobnej stronie.

2. Obliczenia

Przy pomocy metody najmniejszych kwadratów wyznaczamy parametry A i B wzoru:

Wzór ten przedstawia zależność liniową ln z(d)=ln z(0)*

Aby wyznaczyć liczbowe wartości A i B wygodnie jest sporządzić tabelę w następującej postaci:

n	K	d	z(d)	ln(z)	k2	klnz	lnz(x)
1	0	0	34,15	3,530762586	0	0	3,385576
2	1	0,0028175	32,8975365	3,493397778	1	3,493398
3	2	0,005635	31,7325833	3,457344016	4	6,914688
4	3	0,0084525	30,6189168	3,421618015	9	10,26485
5	4	0,01127	29,4090766	3,381303354	16	13,52521
6	5	0,0140875	28,657357	3,355410197	25	16,77705
7	6	0,016905	27,3990098	3,310506875	36	19,86304
8	7	0,0197225	26,2905335	3,26920893	49	22,88446
9	8	0,02254	24,9309891	3,216111571	64	25,72889
10	9	0,0253575	24,6870478	3,206278727	81	28,85651
suma	45			33,64194205	285	148,3081

Po rozwiązaniu układu równań:

otrzymujemy:

y(k)=3,335+0,00629*k

y(k)	ln(z)
3.53	3.530762586
3.4931	3.493397778
3.4562	3.457344016
3.4193	3.421618015
3.3824	3.381303354
3.3455	3.355410197
3.3086	3.310506875
3.2717	3.26920893
3.2348	3.216111571
3.1979	3.206278727

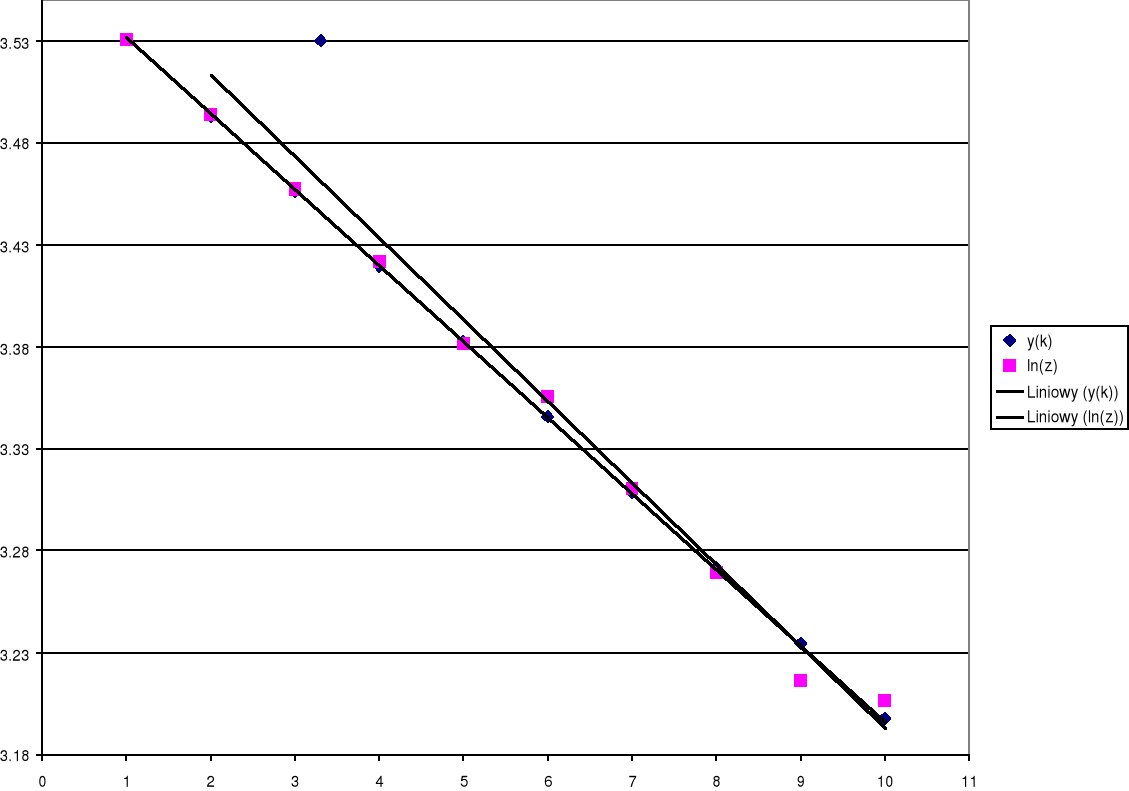
Na podstawie wykresu wyznaczmy d:

Wartość k odczytujemy w wykresu, w naszym przypadku wartość:

k=9,

natomiast d₀, czyli gęstość powierzchniową dla pojedynczej folii wynosi :

d₀=0,00285 [

czyli:

d=0,0252

1. Obliczamy masowy współczynnik pochłaniania dla glinu
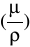
   , czyli:

d₀=0,00285

=0,037 / 0,0028855=12,9597

2. 
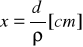
   W celu wyznaczenia grubości nieznanej folii posługujemy się wykresem, w oparciu o który ustalamy d i wyznaczamy grubość folii z zależności:

x=0,0252 / 2,67=0,0094382 [cm]

3. Wnioski

Po przeprowadzeniu obliczeń na podstawie otrzymanych wyników możemy stwierdzić,

że metoda jaką używaliśmy do badania grubości folii aluminiowej pozwala w dość prosty i dokładny sposób określić grubość badanego materiału. Jedynym utrudnieniem jest to że musimy znać gęstość badanego materiału. Doświadczeni wykazało, że istnieje proporcjonalny związek pomiędzy ilością pochłoniętego promieniowania, a grubością folii.

1

7

---