Opis doświadczenia:

Po dokładnym zmierzeniu średnicy kulki oraz przymocowaniu papieru z kalką do płyty odtwarzacza rozpoczęliśmy eksperyment. Kulkę zwalnialiśmy dla trzech różnych prędkości kątowych oraz dwóch różnych wysokości. W rezultacie otrzymaliśmy sześć różnych torów przebiegu kulki (tory te są dołączone do sprawozdania). Prędkości kątowe wyznaczamy korzystając tego, iż zmierzyliśmy czas trwania 20 pełnych obrotów tarczy (dla każdego ustawienia prędkości w odtwarzaczu).

Obliczenia:

Zaczniemy od wyliczenia prędkości kątowych:

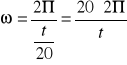
[rad/s]

Prędkość 1:
[rad/s]

Prędkość 2:
[rad/s]

Prędkość 3:
[rad/s]

Masę kulki wyznaczamy dzięki znajomości jej wymiarów i gęstości materiału, z którego jest zrobiona:
[kg]

Poniżej umieszczone są tabelki uzupełniające, na podstawie których wykreślone są wykresy
dla sześciu różnych torów ruchu kulki.

Tor

	5	10	7	2	4	12
R[cm]	4	8	6	2	3	10

Tor

	5	10	15	13	17	7
R[cm]	3	5,5	8	7	9	4

Tor

	16	20	25	8	11	13
R[cm]	7	9	11	4	5	6

Tor

	15	20	40	7	11	23
R[cm]	5	6	11	3	4	7

Tor

	15	20	55	8	25	38
R[cm]	3	4	9,5	2	5	7

Tor

	15	20	60	27	36	47
R[cm]	2	3	7	4	5	6

UWAGA:

Teraz na podstawie wykresów możemy obliczyć tangensy kątów, pamiętając, że obliczamy tangens kątów między wykreśloną prostą a osią
. Wykres dla wygodniejszego nanoszenia danych ma zamienione osie (nie jest zależnością
tylko
).

Wartości kąta zamieniam na miarę w radianach, a promień podstawiam w metrach.

Tangens kąta:
(gdzie x i y to odpowiednie odcinki zaznaczone na wykresie)

dla d1 (dla
):
rad, czyli
= 0,47

dla d2 (dla
):
rad, czyli
= 0,28

dla d3 (dla
):
rad, czyli
= 0,23

dla d4 (dla
):
rad, czyli
= 0,14

dla d5 (dla
):
rad, czyli
= 0,09

dla d6 (dla
):
rad, czyli
= 0,06

Obliczenia siły odśrodkowej:

- zależność od prędkości kątowej płyty odtwarzacza.

Dla wygodnego przedstawienia na wykresie obliczenia wykonujemy dla wartości promienia od 1 do 6 centymetrów.

Obliczenia siły odśrodkowej dla
[rad/s]:

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,001	0,003	0,004	0,005	0,006	0,008

Obliczenia siły odśrodkowej dla
[rad/s]:

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,003	0,006	0,01	0,013	0,016	0,019

Obliczenia siły odśrodkowej dla
[rad/s]:

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,007	0,015	0,022	0,03	0,037	0,045

Obliczenia siły Coriolisa:

- zależność od prędkości początkowej kulki oraz prędkości kątowej płyty odtwarzacza.

Obliczenia wykonujemy dla wartości promienia od 1 do 6 centymetrów (jw.).

Prędkość początkową kulki obliczamy analizując ślad toru jaki zostawiła ona na papierze (przy danej prędkości kątowej i wysokości początkowej). Innymi słowy korzystamy z zależności
, czyli
.

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,122	0,123	0,123	0,123	0,123	0,124

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,073	0,073	0,073	0,074	0,074	0,075

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,151	0,152	0,152	0,153	0,154	0,156

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,092	0,093	0,094	0,096	0,098	0,1

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,136	0,139	0,143	0,148	0,155	0,162

Obliczenia siły Coriolisa dla
[rad/s] i wysokości
:

[m/s]

Promień r [m]	0,01	0,02	0,03	0,04	0,05	0,06
Siła [N]	0,09	0,094	0,01	0,107	0,116	0,126

Na podstawie powyższych tabeli, dla obu sił, można sporządzić odpowiednie wykresy
.

---