Laboratorium

Elektrotechnika i Elektromechanika

Temat: Symulator silnika wykonawczego

prądu stałego.

Automatyka i Robotyka sem III

Grupa 5, sekcja 1

Data odbycia ćwiczenia: 14.01.2010

Bacior Łukasz

Botor Marcin

Czempiel Łukasz

Czerwiński Łukasz

Kokot Damian

Krauze Piotr

Legierski Michał

Morawiec Grzegorz

Mudry Maciej

Salamon Bartłomiej

Spek Damian

Sznapka Piotr

Wyroba Mateusz

1. Wstęp teoretyczny

Do naszej dyspozycji oddano Symulator SWPS , oraz podłączony do niego SWPS.

Silnik był potrzebny do wyznaczenia charakterystyki prędkości kątowej od szerokości impulsu. Dla reszty funkcji symulator korzystał z 2 modeli matematycznych: modelu SWPS oraz modelu PTPS.

Schemat ideowy stanowiska:

Symulator posiadał posiadał następujące możliwości:

1)Dla obiektu rzeczywistego:

1. Sterowanie silnikiem

2. Dla SWPS:

1. Sterowanie twornikowe, stan ustalony, charakterystyka regulacyjna w_r = f(U₂).

2. Sterowanie twornikowe, stan ustalony, charakterystyka mechaniczna M_e= f(w_r).

3. Sterowanie biegunowe, stan ustalony, charakterystyka regulacyjna w_r = f(U₁).

4. Sterowanie biegunowe, stan ustalony, charakterystyka mechaniczna M_e= f(w_r).

5. Sterowanie twornikowe, stan nieustalony

1. Odpowiedź na skok jednostkowy jak dla elementu inercyjnego pierwszego rzędu.

2. Odpowiedź na skok jednostkowy jak dla elementu całkującego z inercją pierwszego rzędu.

6. Sterowanie biegunowe stan nieustalony

1. Odpowiedź na skok jednostkowy.

7. Wizualizacja SWPS

3)Dla PTPS

8. Charakterystyka stanu ustalonego.

1. Z pominięciem oddziaływania twornika i rezystancji przejściowej.

2. Z uwzględnieniem oddziaływania twornika.

3. Z uwzględnieniem rezystancji przejściowej.

4. Z uwzględnieniem oddziaływania twornika i rezystancji przejściowej.

9. Charakterystyka stanu nieustalonego.

1. Odpowiedź na skok jednostkowy jak dla elementu inercyjnego pierwszego rzędu.

2. Odpowiedź na skok jednostkowy jak dla elementu różniczkującego.

Dzięki symulatorowi jesteśmy w stanie zbadać właściwości SWPS i PTPS, nie narażając

ich jednocześnie na uszkodzenie spowodowane np. przyłożeniem zbyt wysokiego napięcia. Pozwala nam on również na sprawdzenie dokładności modeli matematycznych. Wyniki otrzymane z pomocą symulatora możemy porównać z wynikami otrzymanymi, przy testowaniu prawdziwych przetworników.

2. Cel ćwiczenia

Celem tego ćwiczenia laboratoryjnego było rozwiązanie zadanych przez prowadzącego zadań na podstawie wyników uzyskanych z symulatora silnika wykonawczego prądu stałego.

3. Wyniki pomiarów

Zadanie 1.

Rozruch		Hamowanie
Szerokość impulsu	ωr [obr/sek]	Szerokość impulsu	ωr [obr/sek]
34	120	100	2430
36	210	96	2400
44	480	84	2400
51	750	61	1170
68	1350	53	1110
81	1830	51	930
87	2070	47	780
92	2280	44	540
95	2370	40	510
100	2430	37	330
		33	90
		30	0

Zadanie 2.

U2 [V]	ωr [obr/sek]
		Me = 0 [Nm]	Me = 0,5[Nm]	Me = 1 [Nm]
0	0	-88	-176
5	10	-78	-166
10	20	-68	-156
15	30	-58	-146
20	40	-48	-136
25	50	-38	-126
30	60	-28	-116
35	70	-18	-106
40	80	-8	-96
45	90	2	-86
50	100	12	-76
55	110	22	-66
60	120	32	-56
65	130	42	-46
70	140	52	-36
75	150	62	-26
80	160	72	-16
85	170	82	-6
90	180	92	4
95	190	102	14
99	198	110	22

Zadanie 3.

ωr [obr/sek]	Me [Nm]
		U2 = 50 [V]	U2 = 100 [V]	U2 = 150 [V]
0	5,7	11,4	17
5	2,8	8,5	14,2
10	0	5,7	11,4
15	-2,8	2,8	8,5
20	-5,7	0	5,7
25	-8,5	-2,8	2,8
30	-11,4	-5,7	0
35	-14,2	-8,5	-2,8
40	-17	-11,4	-5,7
45	-19,9	-14,2	-8,5
50	-22,7	-17,0	-11,4
55	-25,6	-19,9	-14,2
60	-28,4	-22,7	-17
65	-31,2	-25,6	-19,9
70	-34,1	-28,4	-22,7
75	-36,9	-31,2	-25,6
80	-39,8	-34,1	-28,4
85	-40,3	-36,9	-31,2
90	-45,5	-39,8	-34,1
95	-48,3	-42,6	-36,9
99	-50,6	-44,9	-39,2

Zadanie 4.

U1 [V]	ωr [obr/sek]
		Me= 0 [Nm]	Me= 1 [Nm]	Me= 2 [Nm]	Me= 3 [Nm]	Me= 4 [Nm]
1	5000	-295000	-595000	-895000	-1195000
5	1000	-11000	-23000	-35000	-47000
9	555,6	-3148,1	-6851,9	-10555,6	-14259,3
13	384,6	-1390,5	-3165,7	-4940,8	-6716,0
17	294,1	-743,9	-1782,0	-2820,1	-3858,1
21	238,1	-442,2	-1122,4	-1802,7	-2483,0
25	200,0	-280,0	-760,0	-1240,0	-1720,0
29	172,4	-184,3	-541,0	-897,7	-1254,5
33	151,5	-124,0	-399,4	-674,6	-950,4
37	135,1	-84,0	-303,1	-522,3	-741,4
41	122,0	-56,5	-235,0	-413,4	-591,9
45	111,1	-37,0	-185,2	-333,3	-481,5
49	102,0	-22,9	-147,9	-272,8	-397,8

Zadanie 5.

ωr [obr/sek]	Me [Nm]
		U1 = 100[V]	U1 = 125[V]	U1 = 150[V]	U1 = 175[V]	U1 = 200[V]
0	33,3	41,7	50	58,3	66,7
5	16,7	15,6	12,5	7,3	0
10	0	-10,4	-25	-43,8	-66,7
15	-16,7	-36,5	-62,5	-94,8	-133,3
20	-33,3	-62,5	-100	-145,8	-200,0
25	-50,0	-88,5	-137,5	-196,9	-266,7
30	-66,7	-114,6	-175,0	-247,9	-333,3
35	-83,3	-140,6	-212,5	-299,0	-400,0
40	-100,0	-166,7	-250,0	-350,0	-466,7
45	-116,7	-192,7	-287,5	-401,0	-533,3
49	-130,0	-213,5	-317,5	-441,9	-586,7

Zadanie 6.

T[s]	Wr[Obr/s]	J[Nmsek^2]	U2[V]	R2[Ω]	U1[V]	R1[Ω]	Lm[H]	Mz[Nm]
0	0,0	1,0	100	40	100	60	1,0	2,0
5	9,2	1,0	100	40	100	60	1,0	2,0
10	15,6	1,0	100	40	100	60	1,0	2,0
15	20,2	1,0	100	40	100	60	1,0	2,0
20	23,4	1,0	100	40	100	60	1,0	2,0
25	25,7	1,0	100	40	100	60	1,0	2,0
30	27,3	1,0	100	40	100	60	1,0	2,0
35	28,5	1,0	100	40	100	60	1,0	2,0
40	29,3	1,0	100	40	100	60	1,0	2,0
45	29,8	1,0	100	40	100	60	1,0	2,0
50	30,2	1,0	100	40	100	60	1,0	2,0
55	30,5	1,0	100	40	100	60	1,0	2,0
60	30,7	1,0	100	40	100	60	1,0	2,0
65	30,9	1,0	100	40	100	60	1,0	2,0
70	31,0	1,0	100	40	100	60	1,0	2,0
75	31,0	1,0	100	40	100	60	1,0	2,0
80	31,1	1,0	100	40	100	60	1,0	2,0
85	31,1	1,0	100	40	100	60	1,0	2,0
90	31,1	1,0	100	40	100	60	1,0	2,0
95	31,2	1,0	100	40	100	60	1,0	2,0
96	31,2	1,0	100	40	100	60	1,0	2,0
97	31,2	1,0	100	40	100	60	1,0	2,0
98	31,2	1,0	100	40	100	60	1,0	2,0
99	31,2	1,0	100	40	100	60	1,0	2,0

Zadanie 7.

t[s]	wr[s^-1]	U1[V]	R1[Ω]	L1[H]	Lm[H]	J[Nm*sek^2]	wro [obr/sek]	R2[Ω]	i10
0	0,0	35	15	50,0	0,2	0,2	70	20	400
1	-0,8	35	15	50,0	0,2	0,2	70	20	400
2	-2,9	35	15	50,0	0,2	0,2	70	20	400
3	-5,7	35	15	50,0	0,2	0,2	70	20	400
4	-8,8	35	15	50,0	0,2	0,2	70	20	400
5	-11,9	35	15	50,0	0,2	0,2	70	20	400
6	-15,0	35	15	50,0	0,2	0,2	70	20	400
7	-18,0	35	15	50,0	0,2	0,2	70	20	400
8	-20,7	35	15	50,0	0,2	0,2	70	20	400
9	-23,2	35	15	50,0	0,2	0,2	70	20	400
10	-25,5	35	15	50,0	0,2	0,2	70	20	400
11	-27,5	35	15	50,0	0,2	0,2	70	20	400
12	-29,3	35	15	50,0	0,2	0,2	70	20	400
13	-30,8	35	15	50,0	0,2	0,2	70	20	400
14	-32,2	35	15	50,0	0,2	0,2	70	20	400
15	-33,4	35	15	50,0	0,2	0,2	70	20	400
16	-34,5	35	15	50,0	0,2	0,2	70	20	400
17	-35,4	35	15	50,0	0,2	0,2	70	20	400
18	-36,1	35	15	50,0	0,2	0,2	70	20	400
19	-36,8	35	15	50,0	0,2	0,2	70	20	400
20	-37,4	35	15	50,0	0,2	0,2	70	20	400
21	-37,9	35	15	50,0	0,2	0,2	70	20	400
22	-38,3	35	15	50,0	0,2	0,2	70	20	400
23	-38,7	35	15	50,0	0,2	0,2	70	20	400
24	-39,0	35	15	50,0	0,2	0,2	70	20	400
25	-39,3	35	15	50,0	0,2	0,2	70	20	400
26	-39,5	35	15	50,0	0,2	0,2	70	20	400
27	-39,7	35	15	50,0	0,2	0,2	70	20	400
28	-39,9	35	15	50,0	0,2	0,2	70	20	400
29	-40,0	35	15	50,0	0,2	0,2	70	20	400
30	-40,1	35	15	50,0	0,2	0,2	70	20	400
31	-40,2	35	15	50,0	0,2	0,2	70	20	400
32	-40,3	35	15	50,0	0,2	0,2	70	20	400
33	-40,4	35	15	50,0	0,2	0,2	70	20	400
34	-40,5	35	15	50,0	0,2	0,2	70	20	400
35	-40,5	35	15	50,0	0,2	0,2	70	20	400

Zadanie 8.

Wr[obr/sek]	U2[V]	R2[Ω]	Fi1	C1	Robc[Ω]	C2	I2	Rszcz[Ω]
0	-16,5	28	0,8	5	34	2	2,0	25
7	-0,5	28	0,8	5	34	2	2,0	25
14	4,4	28	0,8	5	34	2	2,0	25
21	6,8	28	0,8	5	34	2	2,0	25
28	8,2	28	0,8	5	34	2	2,0	25
35	9,1	28	0,8	5	34	2	2,0	25

Wr[obr/sek]	U2[V]	R2[Ω]	Fi1	C1	Robc[Ω]	C2	I2	Rszcz[Ω]
0	-38	28	0,8	5	34	2	2,0	30
7	3	28	0,8	5	34	2	2,0	30
14	7	28	0,8	5	34	2	2,0	30
21	9	28	0,8	5	34	2	2,0	30
28	10	28	0,8	5	34	2	2,0	30
35	11	28	0,8	5	34	2	2,0	30

Wr[obr/sek]	U2[V]	R2[Ω]	Fi1	C1	Robc[Ω]	C2	I2	Rszcz[Ω]
0	-48	28	0,8	5	34	2	2,0	40
7	0	28	0,8	5	34	2	2,0	40
14	6	28	0,8	5	34	2	2,0	40
21	8	28	0,8	5	34	2	2,0	40
28	10	28	0,8	5	34	2	2,0	40
35	10	28	0,8	5	34	2	2,0	40

Wr[obr/sek]	U2[V]	R2[Ω]	Fi1	C1	Robc[Ω]	C2	I2	Rszcz[Ω]
0	-59	28	0,8	5	34	2	2,0	50
7	-2	28	0,8	5	34	2	2,0	50
14	5	28	0,8	5	34	2	2,0	50
21	8	28	0,8	5	34	2	2,0	50
28	9	28	0,8	5	34	2	2,0	50
35	10	28	0,8	5	34	2	2,0	50

Wr[obr/sek]	U2[V]	R2[Ω]	Fi1	C1	Robc[Ω]	C2	I2	Rszcz[Ω]
0	-117	28	0,8	5	34	2	2,0	100
7	-15	28	0,8	5	34	2	2,0	100
14	-2	28	0,8	5	34	2	2,0	100
21	3	28	0,8	5	34	2	2,0	100
28	5	28	0,8	5	34	2	2,0	100
35	7	28	0,8	5	34	2	2,0	100

Zadanie 9.

T[s]	U2[V]	U1[V]	R1[Ω]	Robc[Ω]	L12[H]	wr[obr/sek]	R2[Ω]	L2[H]
0	0,0	40	40	30	2,0	50	10	50,0
1	41,3	40	40	30	2,0	50	10	50,0
2	59,9	40	40	30	2,0	50	10	50,0
3	68,2	40	40	30	2,0	50	10	50,0
4	71,9	40	40	30	2,0	50	10	50,0
5	73,6	40	40	30	2,0	50	10	50,0
6	74,4	40	40	30	2,0	50	10	50,0
7	74,7	40	40	30	2,0	50	10	50,0
8	74,9	40	40	30	2,0	50	10	50,0
9	74,9	40	40	30	2,0	50	10	50,0
10	75,0	40	40	30	2,0	50	10	50,0
11	75,0	40	40	30	2,0	50	10	50,0
12	75,0	40	40	30	2,0	50	10	50,0
13	75,0	40	40	30	2,0	50	10	50,0
14	75,0	40	40	30	2,0	50	10	50,0
15	75,0	40	40	30	2,0	50	10	50,0
16	75,0	40	40	30	2,0	50	10	50,0
17	75,0	40	40	30	2,0	50	10	50,0
18	75,0	40	40	30	2,0	50	10	50,0
19	75,0	40	40	30	2,0	50	10	50,0
20	75,0	40	40	30	2,0	50	10	50,0

4. Obliczenia i wykresy

Zadanie 1.

Naszym zadaniem było przeprowadzenie pomiaru prędkości dla różnych wartości szerokości impulsu i wyznaczenie charakterystyki ω_r = f(SzerImp).

Stan ustalony silnika wykonawczego prądu stałego jest opisany za pomocą następujących równań:

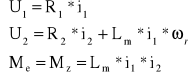
Zadanie 2.

Naszym zadaniem było wyznaczenie zależności ω_r = f (U₂) , przy sterowaniu twornikowym, dla trzech różnych wartości momentów elektromagnetycznych M_e.

Danymi w zadaniu były:

R₁ = 400 [Ω] ; U₁ = 100 [V] = const ; R₂ = 44 [Ω] ; U₂ = 0 - 100 [V] = var ; L_m = 2 [H]

Zależność ω_r = f(U₂) jest opisana wzorem:

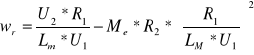
Zadanie 3.

Tym razem naszym zadaniem było wyznaczenie zależności M_e = f(ω_r), przy sterowaniu twornikowym, dla trzech różnych wartości napięć twornika U₂ oraz wyliczenie współczynnika tłumienia wewnętrznego D

Danymi w zadaniu były:

R₁ = 400 [Ω] ; U₁ = 100 [V] = const ; R₂ = 44 [Ω] ; L_m = 20 [H]

Zależność M_e = f(ω_r) jest opisana wzorem:

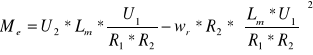
Natomiast współczynnik tłumienia wewnętrznego :

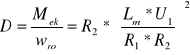
I wynosi on : D = 0,56

Zadanie 4.

Kolejne nasze zadanie polegało na wyznaczeniu zależności ω_r = f(U₁), przy sterowaniu biegunowym, dla pięciu różnych wartości momentów elektromagnetycznych M_e.

Danymi w zadaniu były wartości:

R₁ = 100 [Ω] ; U₁ = 50 [V] = var ; R₂ = 30 [Ω], ; U₂ = 50 [V] = const ; L_m = 1 [H]

Zależność ω_r = f(U₁) jest opisana wzorem:

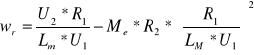
Zadanie 5.

Celem tego zadania było wyznaczenie charakterystyki M_e = f(ω_r), przy sterowaniu biegunowym, dla pięciu różnych wartości napięć wzbudzenia U₁.

Danymi w zadaniu były wielkości:

R₁ = 100 [Ω] ; R₂ = 30 [Ω] ; U₂ = 100 [V] = const ; L_m = 10 [H]

Zależność M_e = f(ω_r) jest opisana wzorem:

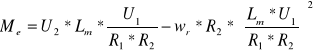
Zadanie 6.

Naszym zadaniem było wyznaczenie elektromechanicznej stałej czasowej silnika przy sterowaniu twornikowym dla następujących danych:

U₁=100 [V] ; 100 [V] ; R₁=60 [Ω] ; R₂=40 [Ω] ; L=1 [H] ; M=2 [Nm] ; J=1 [Nmsek­­_­­­²]

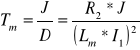
Wyliczone ze wzoru :T_m= 14,5

Zadanie 7.

Celem tego zadania było dobranie parametrów dla prądnicy tachometrycznej,

tak, aby na wykresie funkcji ωr(t), można było zauważyć obie stałe czasowe.

Związane z nimi styczne, oraz same wartości stałych wyznaczono graficznie.

Pierwsza stała czasowa ma w przybliżeniu wartość 1,7 [s], druga około 6[s].

Zadanie 8.

Celem zadania było zaobserwowanie wpływu rezystancji przejścia i oddziaływanie twornika na charakterystykę wyjściową prądnicy tachometrycznej.

Na podstawie danych z instrukcji oraz następujących wzorów wyznaczyliśmy zależność napięcia wyjściowego od prędkości kątowej, uwzględniając różne wartości rezystancji przejścia.

E_rot = C1 ^.ω_r ^.φ

Me = C2 ^.ω_r ^.φ

U_tw = E_rot /(1 + (R_szcz/R_obc))

I_tw = U_tw/R_szcz

U_wy = Erot - I_tw ^.R_obc

Rszcz	Erot	Me	Utw	Itw	Uwy
25	0	3,2	0	0	0
25	28	3,2	16,13559	0,645424	6,055593
25	56	3,2	32,27119	1,290847	12,11119
25	84	3,2	48,40678	1,936271	18,16678
25	112	3,2	64,54237	2,581695	24,22237
25	140	3,2	80,67797	3,227119	30,27797
25	172	3,2	99,11864	3,964746	37,19864
30	0	3,2	0	0	0
30	28	3,2	14,875	0,495833	11,14167
30	56	3,2	29,75	0,991667	22,28333
30	84	3,2	44,625	1,4875	33,425
30	112	3,2	59,5	1,983333	44,56667
30	140	3,2	74,375	2,479167	55,70833
40	0	3,2	0	0	0
40	28	3,2	12,86486	0,321622	17,06486
40	56	3,2	25,72973	0,643243	34,12973
40	84	3,2	38,59459	0,964865	51,19459
40	112	3,2	51,45946	1,286486	68,25946
40	140	3,2	64,32432	1,608108	85,32432
50	0	3,2	0	0	0
50	28	3,2	11,33333	0,226667	20,29333
50	56	3,2	22,66667	0,453333	40,58667
50	84	3,2	34	0,68	60,88
50	112	3,2	45,33333	0,906667	81,17333
50	140	3,2	56,66667	1,133333	101,4667
100	0	3,2	0	0	0
100	28	3,2	7,104478	0,071045	25,58448
100	56	3,2	14,20896	0,14209	51,16896
100	84	3,2	21,31343	0,213134	76,75343
100	112	3,2	28,41791	0,284179	102,3379
100	140	3,2	35,52239	0,355224	127,9224

Zadanie 9.

Celem zadania było, dla zadanych parametrów wyznaczenie stałej czasowej. Wyznaczyliśmy ją metodą graficzną, prowadząc styczną do wykresy z jego początku.. Miejsce jej przecięcia z prostą mającą wartość stanu ustalonego , przyjęliśmy za stałą czasową. Jej wartość to ok. 2,4 [s].

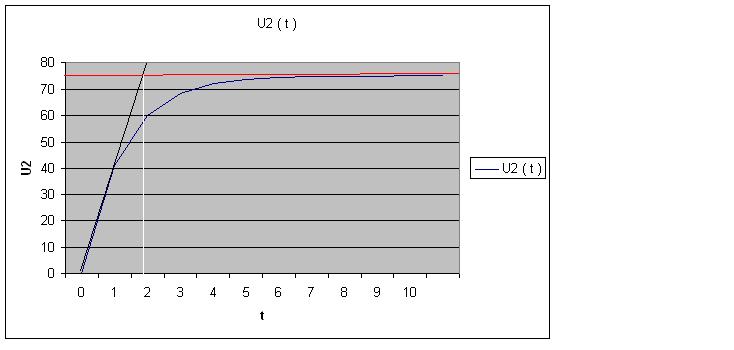
5. Wnioski

Po wykonaniu zadania pierwszego zauważyliśmy że wirnik silnika został wprawiony w ruch, gdy szerokość impulsu wynosiła 34 jednostek, natomiast przestał się obracać gdy szerokości impulsu wynosiła 30 jednostek. Wnioskujemy więc, że wartość szerokości impulsu potrzebna do wprawienia silnika w ruch jest większa niż do utrzymania wirnika w ruchu.

Otrzymana charakterystyka ω_r = f (SzerImp) po lekkim zaproksymowaniu ma charakter liniowy i jest funkcją rosnącą. Dopiero powyżej ok. 90 jednostek następuje mniejszy wzrost prędkości obrotowej. Wynika z tego, że wtedy prędkość obrotowa słabiej zależy od wartości szerokości impulsu.

Charakterystyki otrzymane po wykonaniu zadania drugiego mają charakter liniowy i są funkcjami rosnącymi. Dodatkowo parametr M_e wpływa na te charakterystyki Gdy zwiększaliśmy jego wartość zauważyliśmy obniżanie się wykresu. Jednak współczynnik kierunkowy tych prostych nie uległ zmianie .

Charakterystyki M_e = f(ω_r) wyznaczone w zadaniu trzecim mają charakter liniowy i są to malejące. Ponadto gdy zwiększaliśmy parametr U₂ powodowało to przesuwanie wykresu w górę. Po obliczeniu współczynnika tarcia wewnętrznego stwierdziliśmy że jest on równy tgα (gdzie α jest to kąt nachylenia prostej). Współczynnik ten jest niezależny od zmiennego parametru U₂, dlatego też otrzymane wykresy są do siebie równoległe.

Gdy moment elektromagnetyczny zmniejszymy o połowę, napięcie twornika również musi zmniejszyć się o połowę, aby prędkość obrotowa również zmniejszyła się o połowę

Wynika to z tego, że jeżeli lewą stronę równania zmniejszymy o połowę, to prawą również,

a ponieważ po prawej stronie równania występują dwie wielkości zmienne ω_r i U₂ to dlatego obie te wielkości musimy zmniejszyć o połowę.

Charakterystyki ω_r = f(U₁) uzyskane w zadaniu czwartym mają charakter hiperboliczny, po analizie wykresu doszliśmy do kilku wniosków:

• Charakterystyki te mają dwie asymptoty: pionową U₁=0 oraz poziomą ω_r=0

• Dla M_e=0 wykres zależności ω_r = f(U₁) maleje od +∝ do 0, natomiast dla M_e≥1 wartości rosną od -∝ do 0

• Im mniejsza jest wartość momentu elektromagnetycznego, tym mocniej nachylony jest wykres funkcji ω_r = f(U₁)

Charakterystyki M_e = f(ω_r) wyznaczone w zadaniu piątym są liniowe oraz malejące. wraz ze wzrostem napięcia wzbudzenia (U₁) kąt nachylenia tych prostych względem osi ω_r, ulega zwiększaniu.

Po wykonaniu zadania szóstego oraz analizie informacji uzyskanych na wykładach doszliśmy do wniosku iż moment zewnętrzny wpływa tylko na wielkość odpowiedzi w stanie ustalonym, nie wpływa on na elektromechaniczną stałą czasową czyli nie wpływa na własności dynamiczne.

Gdy rezystancja przejścia jest duża, w granicach 100[Ω], zależność napięcia wyjściowego od prędkości kątowej jest zbliżona do tej dla biegu jałowego. Wynika z tego że dla konkretnych wartości prędkości kątowej, napięcie wyjściowe przyjmuje maksymalne wartości, oraz że wraz ze spadkiem rezystancji przejścia, kolejne wartości napięcia wyjściowego maleją.

Uzyskane przez nas wyniki są prawdziwe dla idealnego silnika wykonawczego prądu stałego. Charakterystyki rzeczywistych silników wykonawczych prądu stałego mogą się różnić zwarzywszy na fakt iż w rzeczywistych maszynach istnieje rezystancja uzwojeń, występują strumienie rozproszenia oraz charakterystyki B = f(H) są nieliniowe. Tak więc uzyskane wyniki mogą być stosowane tylko jako przybliżenia rzeczywistych charakterystyk silników wykonawczych prądu stałego.

3

---