Wydział Geodezji i Kartografii |
Środa 1400-1700 |
Nr zespołu 11 |
||
|
|
|
||
Nazwisko i Imię |
Ocena z przygotowania |
Ocena ze sprawozdania |
Ocena końcowa |
|
1. Biernacka Katarzyna 2. Kędziora Ernest 3. Lentowicz Klaudia
|
|
|
|
|
Prowadzący: dr Przemysław Duda
|
Podpis |
|||
Celem ćwiczenia jest udowodnienie, że częstość rozpadu promieniotwórczego ma charakter rozkładu statystycznego.
Wstęp teoretyczny
Promieniotwórczością nazywamy zjawisko spontanicznej emisji promieniowania jądrowego z jąder atomowych. Znane są trzy podstawowe przemiany promieniotwórcze(α, β, γ).
Przemiana α:
![]()
Przemiana β:
![]()
Przemiana γ:
![]()
W wyniku emisji promieniowania jądrowego zmniejsza się liczba jąder pierwiastka ulegającego rozpadowi.
Liczba jąder które jeszcze nie uległy rozpadowi wyraża się wzorem:
N(t) = N(0)e-λt
gdzie:
λ − współczynnik proporcjonalności, charakteryzujący rodzaj pierwiastka
N(0) − liczba jąder w chwili początkowej t = 0
Można obliczyć prawdopodobieństwo rozpadu dowolnego jądra otrzymując p=λ, z czego wynika, że musi istnieć pewien rozrzut wartości mierzonych wokół średniej.
Rozkład dwumianowy
Przyporządkowując zdarzeniu A o prawdopodobieństwie p liczbę 1, a zdarzeniu przeciwnemu o prawdopodobieństwie 1-p liczbę 0 możemy powiedzieć, że w n zdarzeniach losowych zdarzenie A mogło zajść 0,1,2,…,n razy. W rezultacie zmienna losowa X mogła przyjąć wartości k=0,1,2,…,n, gdzie wyrażenie X=k oznacza, że w n zdarzeniach losowych zdarzenie A zaszło k razy. Funkcję prawdopodobieństwa opisuje wzór:
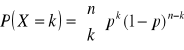
Rozkład Poissona
Jest przybliżeniem rozkładu dwumianowego dla małego p (k<<n). Dla tego warunku, po podstawieniu np.=m i k=x rozkład Poissona przyjmuje postać:
![]()
Rozkład ten jest jednoparametryczny, gdzie parametrem jest wartość oczekiwana m, w naszym przypadku będzie to liczba N, zaś za liniową miarę rozrzutu wartości średniej będziemy przyjmować odchylenie standardowe równe ![]()
.
Rozkład Gaussa
Ten rozkład stosujemy, gdy aktywność naszej próbki wzrasta. Gęstość prawdopodobieństwa dla tego rozkładu wyraża się wzorem: 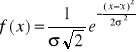
, gdzie 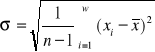
.
Rozkład Gaussa jest zależny od dwóch parametrów, które należy wyznaczyć: średniej wartość liczby zdarzeń ![]()
i odchylenia standardowego ![]()
. Znając te parametry można dla każdej zmiennej losowej wyznaczyć zmienną standaryzowaną ![]()
, zaś prawdopodobieństwo otrzymania wartości x w przedziale (x, x+dx) obliczymy poprzez pomnożenie szerokości przedziału dx przez gęstość prawdopodobieństwa 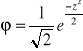
.
Test ![]()
Służy do ilościowej oceny zgodności serii pomiarów z krzywą teoretyczną, która powinna opisywać uzyskane punkty doświadczalne. Zmienna losowa ![]()
podlega rozkładowi prawdopodobieństwa o gęstości 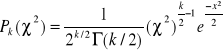
, gdzie k jest liczbą stopni swobody, a ![]()
oznacza funkcję gamma Eulera. Wartość oczekiwana ![]()
równa jest k.
Załóżmy, że przeprowadziliśmy n pomiarów, a zmienną x pogrupowaliśmy w l przedziałach i jeżeli przez ![]()
oznaczymy liczbę zarejestrowanych przez nas zdarzeń ![]()
, wartość teoretyczna ![]()
będzie równa ![]()
. Wtedy :
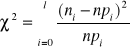
Liczba stopni swobody będzie równa liczbie przedziałów l zmniejszonej o1 oraz o liczbę parametrów s wyznaczających rozkład teoretyczny (s=1 dla rozkładu Poissona, s=2 dla rozkładu Gaussa)
Wyniki i opracowanie pomiarów
Dla ustalonych wartości bramki i liczby prób specjalny program dokonał następujących pomiarów.
Ilość zliczeń |
Bramka [mm] |
Ilość impulsów |
chi kwadrat |
stopnie swobody |
poziom ufności |
średnia |
mediana |
wariancja |
odchylenie stand. |
suma |
||||||||||||
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
500 |
20 |
341 |
129 |
23 |
5 |
1 |
|
|
|
|
|
|
|
|
2,63 |
3 |
0,46 |
0,39 |
0 |
0,41 |
0,64 |
194 |
500 |
20 |
342 |
129 |
24 |
2 |
|
|
|
|
|
|
|
|
|
0,36 |
2 |
0,89 |
0,37 |
0 |
0,35 |
0,59 |
183 |
500 |
20 |
343 |
121 |
29 |
5 |
|
|
|
|
|
|
|
|
|
2,25 |
2 |
0,35 |
0,39 |
0 |
0,41 |
0,64 |
194 |
5000 |
20 |
3581 |
1178 |
207 |
27 |
3 |
|
|
|
|
|
|
|
|
2,04 |
3 |
0,57 |
0,34 |
0 |
0,35 |
0,59 |
1689 |
500 |
50 |
221 |
169 |
78 |
25 |
6 |
1 |
|
|
|
|
|
|
|
1,96 |
4 |
0,74 |
0,86 |
1 |
0,92 |
0,96 |
429 |
500 |
100 |
91 |
141 |
122 |
72 |
49 |
15 |
7 |
1 |
1 |
|
|
|
|
4,18 |
7 |
0,13 |
1,86 |
2 |
2,15 |
1,47 |
929 |
500 |
200 |
17 |
55 |
99 |
100 |
76 |
74 |
39 |
21 |
11 |
5 |
2 |
1 |
|
8,94 |
10 |
0,54 |
3,54 |
3 |
4 |
2 |
1772 |
500 |
500 |
5 |
28 |
56 |
93 |
94 |
82 |
53 |
43 |
24 |
13 |
5 |
3 |
1 |
3,96 |
11 |
0,97 |
4,46 |
4 |
4,65 |
2,16 |
2228 |
500 |
1000 |
8 |
30 |
57 |
84 |
102 |
89 |
56 |
39 |
23 |
8 |
3 |
1 |
|
3,44 |
10 |
0,97 |
4,31 |
4 |
4,1 |
2,03 |
2155 |
500 |
2000 |
6 |
32 |
67 |
68 |
96 |
82 |
55 |
41 |
29 |
11 |
10 |
1 |
2 |
17,01 |
11 |
0,11 |
4,49 |
4 |
5,09 |
2,26 |
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rozkłady Poissona
1. Dla liczby zliczeń 500 i bramki 100mm
Norma |
Średnia |
|
|
|
477,0162 |
1,762639 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment (E) |
Teoria (T) |
(E-T)^2 |
Błąd |
0 |
91 |
81,8518582 |
83,6885 |
9,54 |
1 |
141 |
144,275318 |
10,72771 |
11,87 |
2 |
122 |
127,152686 |
26,55018 |
11,05 |
3 |
72 |
74,7081155 |
7,33389 |
8,49 |
4 |
49 |
32,9208687 |
258,5385 |
7,00 |
5 |
15 |
11,6055247 |
11,52246 |
3,87 |
6 |
7 |
3,40939268 |
12,89246 |
2,65 |
7 |
1 |
0,85850431 |
0,020021 |
1,00 |
8 |
1 |
0,1891542 |
0,657471 |
1,00 |
|
|
|
|
|
Suma |
499 |
|
411,9312 |
|
500-100 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
91 |
0,18 |
81,85 |
1,02 |
9,54 |
||||
1 |
141 |
0,28 |
144,28 |
0,07 |
11,87 |
||||
2 |
122 |
0,24 |
127,15 |
0,21 |
11,05 |
||||
3 |
72 |
0,14 |
74,71 |
0,10 |
8,49 |
||||
4 |
49 |
0,10 |
32,92 |
7,85 |
7,00 |
||||
5 |
15 |
0,03 |
11,61 |
0,99 |
3,87 |
||||
6 |
7 |
0,01 |
3,41 |
3,78 |
2,65 |
||||
7 |
1 |
0,00 |
0,86 |
0,02 |
1,00 |
||||
8 |
1 |
0,00 |
0,19 |
3,48 |
1,00 |
||||
Suma |
499 |
|
|
|
|
||||
liczba pomiarów |
|
499 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedynczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
55,44 |
||||||||
|
|
|
|
||||||
suma testu X |
|
17,53 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
7 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
2. Dla liczby zliczeń 500 i bramki 50 mm
Norma |
Średnia |
|
|
|
489,4681 |
0,81011042 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
221 |
217,719776 |
10,75987 |
14,87 |
1 |
169 |
176,377058 |
54,42098 |
13,00 |
2 |
78 |
71,4424458 |
43,00152 |
8,83 |
3 |
25 |
19,2920898 |
32,58024 |
5,00 |
4 |
6 |
3,90718072 |
4,379893 |
2,45 |
5 |
1 |
0,63304956 |
0,134653 |
1,00 |
Suma |
500 |
|
145,2772 |
|
500-50 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
221 |
0,44 |
217,72 |
0,05 |
14,87 |
||||
1 |
169 |
0,34 |
176,38 |
0,31 |
13,00 |
||||
2 |
78 |
0,16 |
71,44 |
0,60 |
8,83 |
||||
3 |
25 |
0,05 |
19,29 |
1,69 |
5,00 |
||||
4 |
6 |
0,01 |
3,91 |
1,12 |
2,45 |
||||
5 |
1 |
0,00 |
0,63 |
0,21 |
1,00 |
||||
Suma |
500 |
|
|
|
|
||||
liczba pomiarów |
|
500 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
83,33 |
||||||||
|
|
|
|
||||||
suma testu X |
|
3,98 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
4 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
3. Dla liczby zliczeń 5000 i bramki 20mm.
Norma |
Średnia |
|
|
|
4981,057 |
0,33019937 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
3581 |
3580,28633 |
0,509326 |
59,84 |
1 |
1178 |
1182,20828 |
17,70964 |
34,32 |
2 |
207 |
195,182214 |
139,6601 |
14,39 |
3 |
27 |
21,4830145 |
30,43713 |
5,20 |
4 |
3 |
1,77341945 |
1,5045 |
1,73 |
|
|
|
|
|
Suma |
4996 |
|
189,8207 |
|
5000-20 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
3581 |
0,72 |
3580,29 |
0,00 |
59,84 |
||||
1 |
1178 |
0,24 |
1182,21 |
0,01 |
34,32 |
||||
2 |
207 |
0,04 |
195,18 |
0,72 |
14,39 |
||||
3 |
27 |
0,01 |
21,48 |
1,42 |
5,20 |
||||
4 |
3 |
0,00 |
1,77 |
0,85 |
1,73 |
||||
Suma |
4996 |
|
|
|
|
||||
liczba pomiarów |
|
4996 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
99,80 |
||||||||
|
|
|
|
||||||
suma testu X |
|
3,00 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
3 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
4. Dla liczby zliczeń 500 i bramki 20mm.
Norma |
Średnia |
|
|
|
497,3524 |
0,37725919 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
341 |
341,053579 |
0,002871 |
18,46619 |
1 |
129 |
128,665598 |
0,111825 |
11,35782 |
2 |
23 |
24,2701397 |
1,613255 |
4,795832 |
3 |
5 |
3,05204443 |
3,794531 |
2,236068 |
4 |
1 |
0,28785295 |
0,507153 |
1 |
|
|
|
|
|
Suma |
499 |
|
6,029635 |
|
500-20 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
341 |
0,68 |
341,05 |
0,00 |
18,47 |
||||
1 |
129 |
0,26 |
128,67 |
0,00 |
11,36 |
||||
2 |
23 |
0,05 |
24,27 |
0,07 |
4,80 |
||||
3 |
5 |
0,01 |
3,05 |
1,24 |
2,24 |
||||
4 |
1 |
0,00 |
0,29 |
1,76 |
1,00 |
||||
Suma |
499 |
|
|
|
|
||||
liczba pomiarów |
|
499 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
99,80 |
||||||||
|
|
|
|
||||||
suma testu X |
|
3,07 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
3 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
5. Dla liczby zliczeń 500 i bramki 200 mm
Norma |
Średnia |
|||||
481,6684 |
3,439694 |
|||||
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
||
0 |
17 |
15,449267 |
2,404773 |
4,123106 |
||
1 |
55 |
53,140758 |
3,456781 |
7,416198 |
||
2 |
99 |
91,3939852 |
57,85146 |
9,949874 |
||
3 |
100 |
104,789128 |
22,93575 |
10 |
||
4 |
76 |
90,1106456 |
199,1103 |
8,717798 |
||
5 |
74 |
61,9906176 |
144,2253 |
8,602325 |
||
6 |
39 |
35,5381306 |
11,98454 |
6,244998 |
||
7 |
21 |
17,4629015 |
12,51107 |
4,582576 |
||
8 |
11 |
7,50838069 |
12,19141 |
3,316625 |
||
9 |
5 |
2,86961504 |
4,53854 |
2,236068 |
||
10 |
2 |
0,9870599 |
1,026048 |
1,414214 |
||
11 |
1 |
0,30865313 |
0,47796 |
1 |
||
|
|
|
|
|
||
Suma |
500 |
|
466,6714 |
|
||
500-200 |
|
|
|
|
||
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
17 |
0,03 |
15,45 |
0,16 |
4,12 |
||||
1 |
55 |
0,11 |
53,14 |
0,07 |
7,42 |
||||
2 |
99 |
0,20 |
91,39 |
0,63 |
9,95 |
||||
3 |
100 |
0,20 |
104,79 |
0,22 |
10,00 |
||||
4 |
76 |
0,15 |
90,11 |
2,21 |
8,72 |
||||
5 |
74 |
0,15 |
61,99 |
2,33 |
8,60 |
||||
6 |
39 |
0,08 |
35,54 |
0,34 |
6,24 |
||||
7 |
21 |
0,04 |
17,46 |
0,72 |
4,58 |
||||
8 |
11 |
0,02 |
7,51 |
1,62 |
3,32 |
||||
9 |
5 |
0,01 |
2,87 |
1,58 |
2,24 |
||||
10 |
2 |
0,00 |
0,99 |
1,04 |
1,41 |
||||
11 |
1 |
0,00 |
0,31 |
1,55 |
1,00 |
||||
Suma |
500 |
|
|
|
|
||||
liczba pomiarów |
|
500 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
41,67 |
||||||||
|
|
|
|
||||||
suma testu X |
|
12,46 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
11 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
6. Dla liczby zliczeń 500 i bramki 500 mm
Norma |
Średnia |
|
|
|
|
493,8904 |
4,36752366 |
|
|
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
|
0 |
5 |
6,26381788 |
1,597236 |
2,236068 |
|
1 |
28 |
27,3573728 |
0,41297 |
5,291503 |
|
2 |
56 |
59,7419865 |
14,00246 |
7,483315 |
|
3 |
93 |
86,9748464 |
36,30248 |
9,643651 |
|
4 |
94 |
94,9661748 |
0,933494 |
9,69536 |
|
5 |
82 |
82,9534031 |
0,908977 |
9,055385 |
|
6 |
53 |
60,3834917 |
54,51595 |
7,28011 |
|
7 |
43 |
37,6751898 |
28,3536 |
6,557439 |
|
8 |
24 |
20,5684104 |
11,77581 |
4,898979 |
|
9 |
13 |
9,98144653 |
9,111665 |
3,605551 |
|
10 |
5 |
4,35942039 |
0,410342 |
2,236068 |
|
11 |
3 |
1,73089743 |
1,610621 |
1,732051 |
|
12 |
1 |
0,62997795 |
0,136916 |
1 |
|
|
|
||||
Suma |
500 |
|
160,0725 |
|
|
500-500 |
|
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
5 |
0,01 |
6,26 |
0,25 |
2,24 |
||||
1 |
28 |
0,06 |
27,36 |
0,02 |
5,29 |
||||
2 |
56 |
0,11 |
59,74 |
0,23 |
7,48 |
||||
3 |
93 |
0,19 |
86,97 |
0,42 |
9,64 |
||||
4 |
94 |
0,19 |
94,97 |
0,01 |
9,70 |
||||
5 |
82 |
0,16 |
82,95 |
0,01 |
9,06 |
||||
6 |
53 |
0,11 |
60,38 |
0,90 |
7,28 |
||||
7 |
43 |
0,09 |
37,68 |
0,75 |
6,56 |
||||
8 |
24 |
0,05 |
20,57 |
0,57 |
4,90 |
||||
9 |
13 |
0,03 |
9,98 |
0,91 |
3,61 |
||||
10 |
5 |
0,01 |
4,36 |
0,09 |
2,24 |
||||
11 |
3 |
0,01 |
1,73 |
0,93 |
1,73 |
||||
12 |
1 |
0,00 |
0,63 |
0,22 |
1,00 |
||||
Suma |
500 |
|
|
|
|
||||
liczba pomiarów |
|
500 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
38,46 |
||||||||
|
|
|
|
||||||
suma testu X |
|
5,33 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
11 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
7. Dla liczby zliczeń 500 i bramki 1000 mm
Norma |
Średnia |
|
|
|
504,0796 |
4,39241272 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
8 |
6,23589122 |
3,11208 |
2,828427 |
1 |
30 |
27,3906079 |
6,808927 |
5,477226 |
2 |
57 |
60,1554274 |
9,956722 |
7,549834 |
3 |
84 |
88,0758216 |
16,61232 |
9,165151 |
4 |
102 |
96,7163398 |
27,91707 |
10,0995 |
5 |
89 |
84,9636163 |
16,29239 |
9,433981 |
6 |
56 |
62,1992115 |
38,43022 |
7,483315 |
7 |
39 |
39,0292297 |
0,000854 |
6,244998 |
8 |
23 |
21,4290606 |
2,46785 |
4,795832 |
9 |
8 |
10,4583643 |
6,043555 |
2,828427 |
10 |
3 |
4,59374524 |
2,540024 |
1,732051 |
11 |
1 |
1,83432955 |
0,696106 |
1 |
|
|
|
|
|
Suma |
500 |
|
130,8781 |
|
500-1000 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
8 |
0,02 |
6,24 |
0,50 |
2,83 |
||||
1 |
30 |
0,06 |
27,39 |
0,25 |
5,48 |
||||
2 |
57 |
0,11 |
60,16 |
0,17 |
7,55 |
||||
3 |
84 |
0,17 |
88,08 |
0,19 |
9,17 |
||||
4 |
102 |
0,20 |
96,72 |
0,29 |
10,10 |
||||
5 |
89 |
0,18 |
84,96 |
0,19 |
9,43 |
||||
6 |
56 |
0,11 |
62,20 |
0,62 |
7,48 |
||||
7 |
39 |
0,08 |
39,03 |
0,00 |
6,24 |
||||
8 |
23 |
0,05 |
21,43 |
0,12 |
4,80 |
||||
9 |
8 |
0,02 |
10,46 |
0,58 |
2,83 |
||||
10 |
3 |
0,01 |
4,59 |
0,55 |
1,73 |
||||
11 |
1 |
0,00 |
1,83 |
0,38 |
1,00 |
||||
Suma |
500 |
|
|
|
|
||||
liczba pomiarów |
|
500 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
41,67 |
||||||||
|
|
|
|
||||||
suma testu X |
|
3,83 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
10 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
8. Dla liczy zliczeń 500 i bramki 2000 mm
Norma |
Średnia |
|
|
|
480,3255 |
4,43975257 |
|
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
6 |
5,66729236 |
0,110694 |
2,44949 |
1 |
32 |
25,1613758 |
46,76678 |
5,656854 |
2 |
67 |
55,8551415 |
124,2079 |
8,185353 |
3 |
68 |
82,6610027 |
214,945 |
8,246211 |
4 |
96 |
91,7485998 |
18,0744 |
9,797959 |
5 |
82 |
81,4682164 |
0,282794 |
9,055385 |
6 |
55 |
60,2831205 |
27,91136 |
7,416198 |
7 |
41 |
38,2345913 |
7,647485 |
6,403124 |
8 |
29 |
21,2190157 |
60,54372 |
5,385165 |
9 |
11 |
10,4674644 |
0,283594 |
3,316625 |
10 |
10 |
4,64729518 |
28,65145 |
3,162278 |
11 |
1 |
1,8757128 |
0,766873 |
1 |
12 |
2 |
0,69397506 |
1,705701 |
1,41424 |
|
|
|
|
|
Suma |
500 |
|
531,8977 |
|
500-2000 |
500 |
|
531,8977 |
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
||||
0 |
6 |
0,01 |
5,67 |
0,02 |
2,45 |
||||
1 |
32 |
0,06 |
25,16 |
1,86 |
5,66 |
||||
2 |
67 |
0,13 |
55,86 |
2,22 |
8,19 |
||||
3 |
68 |
0,14 |
82,66 |
2,60 |
8,25 |
||||
4 |
96 |
0,19 |
91,75 |
0,20 |
9,80 |
||||
5 |
82 |
0,16 |
81,47 |
0,00 |
9,06 |
||||
6 |
55 |
0,11 |
60,28 |
0,46 |
7,42 |
||||
7 |
41 |
0,08 |
38,23 |
0,20 |
6,40 |
||||
8 |
29 |
0,06 |
21,22 |
2,85 |
5,39 |
||||
9 |
11 |
0,02 |
10,47 |
0,03 |
3,32 |
||||
10 |
10 |
0,02 |
4,65 |
6,17 |
3,16 |
||||
11 |
1 |
0,00 |
1,88 |
0,41 |
1,00 |
||||
12 |
2 |
0,00 |
0,69 |
2,46 |
1,41 |
||||
Suma |
500 |
|
|
|
|
||||
liczba pomiarów |
|
500 |
|||||||
|
|
|
|
||||||
średnia niepewność pojedyńczego pomiaru |
|
||||||||
|
|
|
|
||||||
średnia arytmetyczna ilości rozpadów w czasie |
38,46 |
||||||||
|
|
|
|
||||||
suma testu X |
|
19,48 |
|||||||
|
|
|
|
||||||
liczba stopni swobody |
|
11 |
|||||||
|
|
|
|
||||||
prawdopodobieństwo |
|
0,95 |
|||||||
Rozkłady Gaussa
1. Dla liczby zliczeń 500 i bramki 500 mm
Odchylenie |
Norma |
Średnia |
|||
2,105504 |
497,32419 |
4,1020014 |
|||
|
|
|
|||
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
|
0 |
5 |
14,13 |
83,267347 |
2,236068 |
|
1 |
28 |
31,83 |
14,683379 |
5,2915026 |
|
2 |
56 |
57,25 |
1,560101 |
7,4833148 |
|
3 |
93 |
82,17 |
117,30762 |
9,6436508 |
|
4 |
94 |
94,12 |
0,0145059 |
9,6953597 |
|
5 |
82 |
86,04 |
16,311203 |
9,0553851 |
|
6 |
53 |
62,77 |
95,41465 |
7,2801099 |
|
7 |
43 |
36,54 |
41,67787 |
6,5574385 |
|
8 |
24 |
16,98 |
49,283463 |
4,8989795 |
|
9 |
13 |
6,30 |
44,940461 |
3,6055513 |
|
10 |
5 |
1,86 |
9,8393784 |
2,236068 |
|
11 |
3 |
0,44 |
6,5534437 |
1,7320508 |
|
12 |
1 |
0,08 |
0,8410089 |
1 |
|
|
|
|
|
|
|
Suma |
500 |
|
481,69443 |
|
|
500-500 |
|
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
0 |
5 |
0,01 |
14,13 |
1 |
28 |
0,06 |
31,83 |
2 |
56 |
0,11 |
57,25 |
3 |
93 |
0,19 |
82,17 |
4 |
94 |
0,19 |
94,12 |
5 |
82 |
0,16 |
86,04 |
6 |
53 |
0,11 |
62,77 |
7 |
43 |
0,09 |
36,54 |
8 |
24 |
0,05 |
16,98 |
9 |
13 |
0,03 |
6,30 |
10 |
5 |
0,01 |
1,86 |
11 |
3 |
0,01 |
0,44 |
12 |
1 |
0,00 |
0,08 |
Suma |
500 |
|
|
liczba pomiarów |
|
500 |
|
|
|
|
|
średnia niepewność pojedyńczego pomiaru |
|
||
|
|
|
|
średnia arytmetyczna ilości rozpadów w czasie |
38,46 |
||
|
|
|
|
suma testu X |
|
51,02 |
|
|
|
|
|
liczba stopni swobody |
11 |
||
|
|
|
|
prawdopodobieństwo |
|
|
|
2. Dla liczby zliczeń 500 i bramki 1000 mm
Odchylenie |
Norma |
Średnia |
|
|
2,0370681 |
500,5915796 |
4,125073794 |
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
8 |
12,62 |
21,313425 |
2,8284271 |
1 |
30 |
30,22 |
0,04973 |
5,4772256 |
2 |
57 |
56,89 |
0,0110532 |
7,5498344 |
3 |
84 |
84,17 |
0,0284429 |
9,1651514 |
4 |
102 |
97,85 |
17,206375 |
10,099505 |
5 |
89 |
89,40 |
0,1588226 |
9,4339811 |
6 |
56 |
64,18 |
66,993066 |
7,4833148 |
7 |
39 |
36,21 |
7,7612904 |
6,244998 |
8 |
23 |
16,06 |
48,205503 |
4,7958315 |
9 |
8 |
5,59 |
5,7845233 |
2,8284271 |
10 |
3 |
1,53 |
2,1549905 |
1,7320508 |
11 |
1 |
0,33 |
0,4493481 |
1 |
|
|
|
|
|
Suma |
500 |
|
170,11657 |
|
500-1000 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
0 |
8 |
0,02 |
12,62 |
1,689 |
2,83 |
1 |
30 |
0,06 |
30,22 |
0,002 |
5,48 |
2 |
57 |
0,11 |
56,89 |
0,000 |
7,55 |
3 |
84 |
0,17 |
84,17 |
0,000 |
9,17 |
4 |
102 |
0,20 |
97,85 |
0,176 |
10,10 |
5 |
89 |
0,18 |
89,40 |
0,002 |
9,43 |
6 |
56 |
0,11 |
64,18 |
1,044 |
7,48 |
7 |
39 |
0,08 |
36,21 |
0,214 |
6,24 |
8 |
23 |
0,05 |
16,06 |
3,002 |
4,80 |
9 |
8 |
0,02 |
5,59 |
1,034 |
2,83 |
10 |
3 |
0,01 |
1,53 |
1,407 |
1,73 |
11 |
1 |
0,00 |
0,33 |
1,363 |
1,00 |
Suma |
500 |
|
|
|
|
liczba pomiarów |
|
500 |
|
|
|
|
|
|
|
|
|
średnia niepewność pojedyńczego pomiaru |
|
|
|
||
|
|
|
|
|
|
średnia arytmetyczna ilości rozpadów w czasie |
41,67 |
|
|
||
|
|
|
|
|
|
suma testu X |
|
9,93 |
|
|
|
|
|
|
|
|
|
liczba stopni swobody 10 |
|
|
|||
|
|
|
|
|
|
prawdopodobieństwo |
|
|
|
|
|
3. Dla liczby zliczeń 500 i bramki 2000 mm
Odchylenie |
Norma |
Średnia |
|
|
2,28254 |
503,7847732 |
4,173650247 |
|
|
|
|
|
|
|
Zliczenia |
Eksperyment |
Teoria |
(E-T)^2 |
Błąd |
0 |
6 |
16,5468355 |
111,23574 |
2,4494897 |
1 |
32 |
33,49216782 |
2,2265648 |
5,6568542 |
2 |
67 |
55,95173025 |
122,06426 |
8,1853528 |
3 |
68 |
77,1481892 |
83,689366 |
8,2462113 |
4 |
96 |
87,79704635 |
67,288449 |
9,797959 |
5 |
82 |
82,46620851 |
0,2173504 |
9,0553851 |
6 |
55 |
63,93138353 |
79,769612 |
7,4161985 |
7 |
41 |
40,90667039 |
0,0087104 |
6,4031242 |
8 |
29 |
21,60310185 |
54,714102 |
5,3851648 |
9 |
11 |
9,416294826 |
2,5081221 |
3,3166248 |
10 |
10 |
3,38755173 |
43,724472 |
3,1622777 |
11 |
1 |
1,00585129 |
3,424E-05 |
1 |
12 |
2 |
0,246503773 |
3,074749 |
1,4142136 |
|
|
|
|
|
Suma |
500 |
|
570,52153 |
|
500-2000 |
|
|
|
|
xi |
ni |
pi=prawdopodobieństwo wg Gaussa |
normalizacja |
test X |
bład |
0 |
6 |
0,01 |
16,55 |
6,72 |
2,45 |
1 |
32 |
0,06 |
33,49 |
0,07 |
5,66 |
2 |
67 |
0,13 |
55,95 |
2,18 |
8,19 |
3 |
68 |
0,14 |
77,15 |
1,08 |
8,25 |
4 |
96 |
0,19 |
87,80 |
0,77 |
9,80 |
5 |
82 |
0,16 |
82,47 |
0,00 |
9,06 |
6 |
55 |
0,11 |
63,93 |
1,25 |
7,42 |
7 |
41 |
0,08 |
40,91 |
0,00 |
6,40 |
8 |
29 |
0,06 |
21,60 |
2,53 |
5,39 |
9 |
11 |
0,02 |
9,42 |
0,27 |
3,32 |
10 |
10 |
0,02 |
3,39 |
12,91 |
3,16 |
11 |
1 |
0,00 |
1,01 |
0,00 |
1,00 |
12 |
2 |
0,00 |
0,25 |
12,47 |
1,41 |
Suma |
500 |
|
|
|
|
liczba pomiarów |
|
500 |
|
|
|
|
|
|
|
|
|
średnia niepewność pojedynczego pomiaru |
|
|
|
||
|
|
|
|
|
|
średnia arytmetyczna ilości rozpadów w czasie |
38,46 |
|
|
||
|
|
|
|
|
|
suma testu X |
|
40,25 |
|
|
|
|
|
|
|
|
|
liczba stopni swobody |
|
11 |
|
|
|
|
|
|
|
|
|
prawdopodobieństwo |
|
|
|
|
|
Wnioski
Dokonując pomiarów i powyższych obliczeń możemy stwierdzić, że rozpad promieniotwórczy ma zdecydowanie charakter rozkładu statystycznego. Dla początkowych serii rozkładem tym jest rozkład Poissona. Wraz ze zmianą(wzrostem) wartości bramki krzywa teoretyczna również się zmienia i możemy stwierdzić, że w ostatnich trzech seriach mamy do czynienia z rozkładem Gaussa.
-50
0
50
100
150
200
250
300
350
400
0
1
2
3
4
eksperyment
teoria
Wyszukiwarka
Podobne podstrony:
badanie fotokom˘rki2, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
badanie fotokom˘rki1, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
pomiary mikroskopowe, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
fiza iii - 2, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka, fizyka
fiz22art, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka, fizyka
moment bezwadnoci i tw steinera, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
Sprawkozgeolo, Semestr 1, Fizyka
Sprawka OP, 26065943-Sprawozdanie-Tłoczenie, POLITECHNIKA POZNAŃSKA
Sprawka OP, 26065943-Sprawozdanie-Tłoczenie, POLITECHNIKA POZNAŃSKA
lab 14, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka, fizyka
lab7, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka, fizyka
sprawko 34(1)(1), Fizyka
więcej podobnych podstron