Wykonanie:

Sprawozdanie z ćw nr 3

(203)

UKŁADY SEKWENCYJNE

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z podstawowymi elementami sekwencyjnych układów logicznych (przerzutnikami) oraz metodami syntezy złożonych układów sekwencyjnych (rejestry, układy liczników, sumatory szeregowe)

2. Program ćwiczenia:

1. Zaprojektować licznik synchroniczny zliczający w kolejności 0,4,8,12; 1,5,9,13; 2, 6, 9, 13; 2, 7, 10, 15:

Tabela wzbudzeń przerzutnika J-K

Q	Q^+	J	K
0	0	0	-
0	1	1	-
1	0	-	1
1	1	-	0

Tabela :

l.dz.	DCBA	l.dz.	DCBA	JA KA	JB KB	JC KC	JD KD
0	0000	1	0001	0 -	0 -	1 -	0 -
1	0001	2	0010	0 -	0 -	- 1	1 -
2	0010	3	0011	0 -	0 -	1 -	- 0
3	0011	4	0100	1 -	0 -	- 1	- 1
4	0100	5	0101	- 0	0 -	1 -	0 -
5	0101	6	0110	- 0	0 -	- 1	1 -
6	0110	7	0111	- 0	0 -	1 -	- 0
7	0111	8	1000	- 1	1 -	- 1	- 1
8	1000	9	1001	0 -	- 0	1 -	0 -
9	1001	10	1010	0 -	- 0	- 1	1 -
10	1010	11	1011	0 -	- 0	1 -	- 0
11	1011	12	1100	1 -	- 0	- 1	- 1
12	1100	13	1101	- 0	- 0	1 -	0 -
13	1101	14	1110	- 0	- 0	- 1	1 -
14	1110	15	1111	- 0	- 0	1 -	- 0
15	1111	0	0000	- 1	- 1	- 1	- 1

Określenie i minimalizacja funkcji logicznych:

	BA
DC		00	01	11	10
	00	-	0	0	-
	01	-	0	0	-
	11	-	1	1	-
	10	-	0	0	-

	BA
DC		00	01	11	10
	00	0	-	-	0
	01	0	-	-	0
	11	1	-	-	1
	10	0	-	-	0

	BA
DC		00	01	11	10
	00	-	-	0	0
	01	-	-	0	0
	11	-	-	1	0
	10	-	-	0	0

	BA
DC		00	01	11	10
	00	0	0	-	-
	01	0	0	-	-
	11	0	1	-	-
	10	0	0	-	-

	BA
DC		00	01	11	10
	00	-	-	-	-
	01	1	1	1	1
	11	1	1	1	1
	10	-	-	-	-

	BA
DC		00	01	11	10
	00	1	1	1	1
	01	-	-	-	-
	11	-	-	-	-
	10	1	1	1	1

nie zależy
nie zależy

	BA
DC		00	01	11	10
	00	-	-	-	-
	01	-	-	-	-
	11	1	1	1	1
	10	0	0	0	0

	BA
DC		00	01	11	10
	00	0	0	0	0
	01	1	1	1	1
	11	-	-	-	-
	10	-	-	-	-

Układ logiczny :

2. Zaprojektować licznik asynchroniczny mod 7/13:

a. dla mod 13 b. dla mod 7

Cyfra dziesiętna		Kod binarny
0		0 0 0
1		0 0 1
2		0 1 0
3		0 1 1
4		1 0 0
5		1 0 1
6		1 1 0
7		1 1 1
8		1000
9		1001
10		1010
11		1011
12		1100
13		1101
14		Ø
15		Ø
Cyfra dziesiętna		Kod binarny
0		0 0 0
1		0 0 1
2		0 1 0
3		0 1 1
4		1 0 0
5		1 0 1
6		1 1 0
7		1 1 1
8		Ø
9		Ø
10		Ø
11		Ø
12		Ø
13		Ø
14		Ø
15		Ø

Określenie i minimalizacja funkcji logicznych:

a. dla mod 13 b. dla mod 7

	BA
DC		00	01	11	10
	00	0	0	0	0
	01	0	0	0	0
	11	0	1	Ø	Ø
	10	0	0	0	0
	BA
DC		00	01	11	10
	00	0	0	0	0
	01	0	0	1	0
	11	Ø	Ø	Ø	Ø
	10	Ø	Ø	Ø	Ø

Układ logiczny:

Licznik mod 7/13 można również wykonać jako licznik mod N

Układ logiczny:

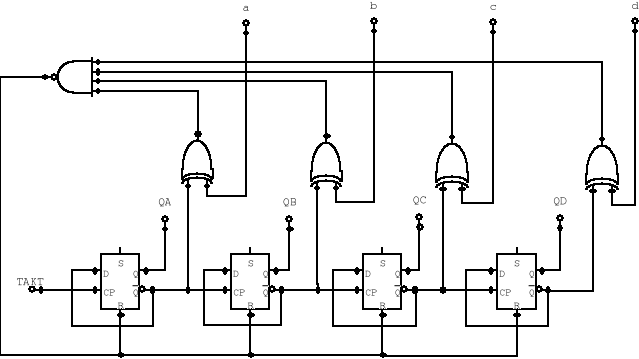
3. Uwagi i wnioski:

Licznik synchroniczny zliczający „co cztery” w rzeczywistości okazał się prosty do zrealizowania. W załączonych tabelach widać sposób projektowania tego układu. Sam układ jak widać na dołączonym schemacie nie jest skomplikowany. Oprócz przerzutników JK wystarczyło użycie tylko dwóch bramek AND.

Licznik mod 7/13 zrealizowaliśmy właściwie z dwóch liczników tj. mod 7 i mod 13. Jak widać na schemacie tego licznika (punkt 2.2) wyjścia bramek „resetujących” (AND - trójwejściowe) połączone są z prostym układem multipleksera o jednym wej. adresowym. Pozwala to na wybranie bramki odpowiedzialnej za repetowanie przerzutników co jest jednoznaczne z wyborem licznika (tj. mod 7 albo mod 13). Jak widać w tym układzie nie można się pomylić i wybrać obydwu liczników naraz. Naszym zdaniem takie rozwiązanie tego zadania jest na pewno przejrzyste (od razu widać jakie elementy za co dopowiadają w układzie) i proste. Drugim sposobem (bardziej uniwersalnym) było zrealizowanie tego licznika z układu licznika mod N. Jeżeli spojrzeć na obydwa układy to jak widać mod N wcale nie jest bardziej skomplikowany.

6

---