(163797) Sylwia Starzyńska
(163769) Michał Luszawski
Temat: Układy kombinacyjne: układy arytmetyczne
(laboratorium dnia 6.11.008)
Cel ćwiczenia
Ćwiczenie ma na celu praktyczne zapoznanie studentów z budową, działaniem, właściwościami oraz syntezą podstawowych układów kombinacyjnych, takich jak: komparatory, sumatory, subtraktory, układy sterujące.
Wstęp teoretyczny
Układ kombinacyjny jest jednym z rodzajów układów cyfrowych. Charakteryzuje się tym, że stan wyjść zależy wyłącznie od stanu wejść; stan wyjść opisują funkcje boolowskie - w przeciwieństwie do układów sekwencyjnych, których stan wyjść zależy od stanu wejść oraz od poprzedniego stanu wyjść.
Układy kombinacyjne:
Komutatory - multiplekser, demultiplekser
Konwertery kodów - koder, dekoder, transkoder
Bloki artymetyczne - sumator, komparator, ALU
Sumator, substraktor.
W przypadku dodawania wielobitowych liczb dwójkowych należy uwzględnić przeniesienie z pozycji sąsiedniej mniej znaczącej od rozpatrywanej.
Komparator.
Układy zwane komparatorami liczb służą do porównywania wartości dwu lub więcej liczb dwójkowych. Komparatory mogą występować w różnych postaciach. Jeżeli A i B są porównywanymi liczbami , to komparator może realizować jedną lub kilka z następujących funkcji: A = B, A < B, A <= B, A > B, A >= B.
Realizowane ćwiczenia
a) Komparator 2-bitowy (2 wyjściowy)
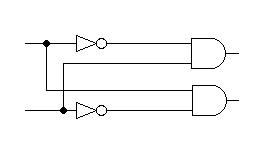
x1 |
x2 |
y1 |
y2 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
b) Komparator 2-bitowy (3 wyjściowy)
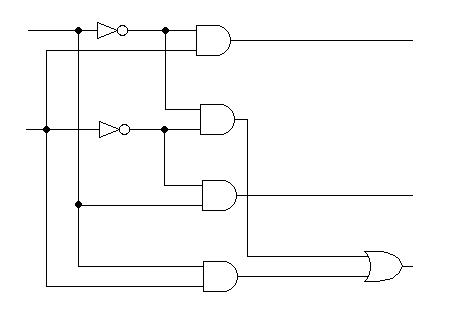
x1 |
x2 |
y1 |
y2 |
y3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
c) Układ, który w zależności od sygnału sterującego realizuje sumę logiczną lub iloczyn logiczny
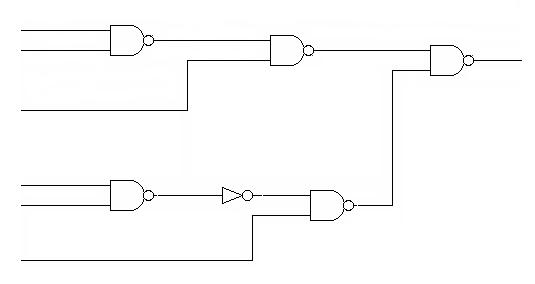
x1 |
x2 |
S |
y1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
d) Sumator 1-bitowy
x1 |
x2 |
C |
C' |
y |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
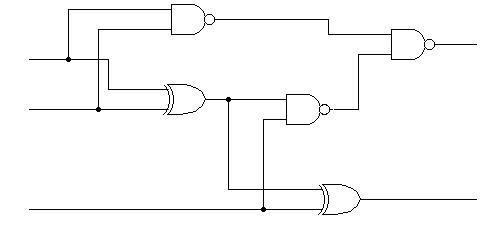
e) Układ odejmujący - subtraktor
x1 |
x2 |
y |
C |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
nr |
z |
x1 |
x2 |
x3 |
y1 |
y2 |
y3 |
y4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
- |
1 |
0 |
0 |
0 |
- |
- |
- |
- |
-1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
-2 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
-3 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
-4 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
-5 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
-6 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
-7 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
f) Układ generujący uzupełnienie do dwóch (kod U2)
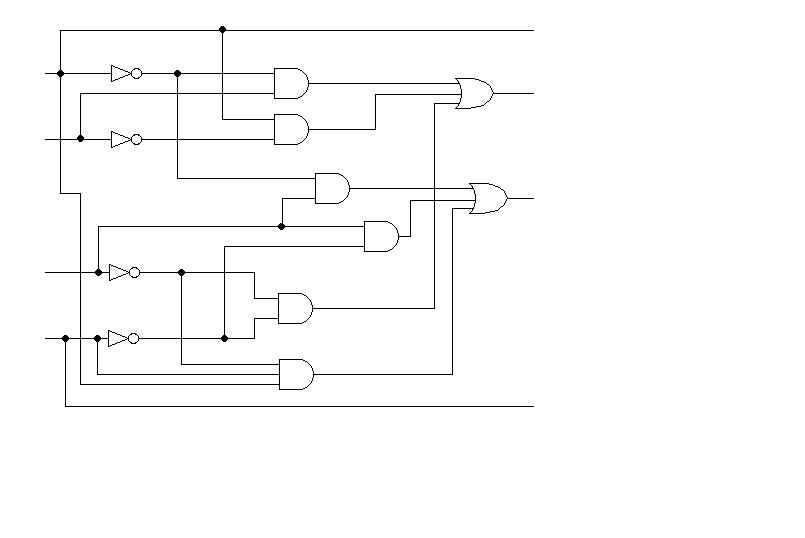
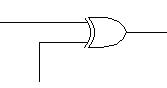
g) Układ, który w zależności od sygnału sterującego daje na wyjściu sygnał wyjściowy lub jego negacje
x1 |
S |
y1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
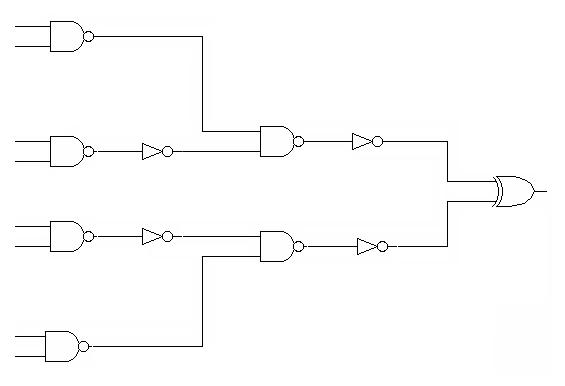
h) Układ sprawdzający, czy liczba jest z przedziału 5:10
x1 |
x2 |
x3 |
x4 |
y |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
4. Wnioski.
Układy kombinacyjne są układami bez pamięci. Układy arytmetyczne wykonują operacje na liczbach binarnych takie same jak w systemie dziesiętnym. Komparatory, to układy logiczne porównujące pary bitów.