ĆWICZENIA 4

MIARY ZMIENNOŚCI (KLASYCZNE)

1. ODCHYLENIE STANDARDOWE

• jest klasyczną miarą zróżnicowania

• stanowi pierwiastek kwadratowy z wariancji (wariancja - średnia arytmetyczna kwadratów odchyleń poszczególnych wartości zbiorowości statystycznej od ich średniej arytmetycznej)

• odchylenie standardowe określa, o ile wszystkie jednostki danej zbiorowości różnią się średnio od średniej arytmetycznej badanej zmiennej

1.1. Szereg szczegółowy, wyliczający

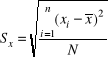
PRZYKŁAD

Płace w grupie 8 robotników przedsiębiorstwa X

410, 425, 440, 455, 465, 480, 490, 520

N = 8;

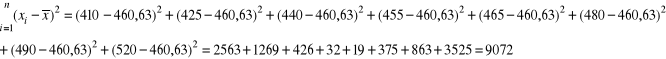
Płaca wszystkich robotników w badanej zbiorowości różni się przeciętnie od średniej płacy (wynoszącej 460,63 zł) o 33,67 zł.

1.2. Szereg rozdzielczy z przedziałami jednowariantowymi

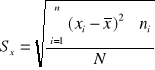
PRZYKŁAD

Płace robotników przedsiębiorstwa K

Płaca	410	425	440	455	465	480	490	520
Liczba robotników	2	4	6	10	9	7	3	1

N=42

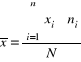
Płaca	410	425	440	455	465	480	490	520
Liczba robotników	2	4	6	10	9	7	3	1
	820	1700	2640	4550	4185	3360	1470	520	=19245

Płaca	410	425	440	455	465	480	490	520
Liczba robotników	2	4	6	10	9	7	3	1
	820	1700	2640	4550	4185	3360	1470	520	=19245
	2324	1103	332	10	46	475	1011	3818
	4648	4412	1992	100	414	3325	3033	38108	=21742

Płace robotników w przedsiębiorstwie K różnią się od średniej płacy (wynoszącej 458,21 zł) przeciętnie o 22,75 zł.

1.3. Szereg rozdzielczy wielowariantowy

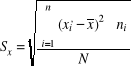
PRZYKŁAD

Płace robotników przedsiębiorstwa Z

Płaca	350-400	400-450	450-500	500-550	550-600	600-650	650-700
Liczba robotników	4	7	9	12	10	8	5

N=55

;

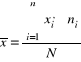
Płaca	350-400	400-450	450-500	500-550	550-600	600-650	650-700
Liczba robotników	4	7	9	12	10	8	5
	375	425	475	525	575	625	675
	1500	2975	4275	6300	5750	5000	3375	=29175

Płaca	350-400	400-450	450-500	500-550	550-600	600-650	650-700
Liczba robotników	4	7	9	12	10	8	5
	24165	11120	3075	30	1985	8940	20895
	96660	77840	27675	360	19850	71520	104475	=398380

Płace robotników w przedsiębiorstwie Z różnią się od średniej płacy (wynoszącej 530,45 zł) przeciętnie o 85,11 zł.

2. WSPÓŁCZYNNIK ZMIENNOŚCI

• stanowi stosunek odchylenia standardowego do średniej arytmetycznej

• wyrażany w procentach

• jeśli wartość współczynnika jest niższa niż 35%, wówczas badana zbiorowość statystyczna z punktu widzenia rozpatrywanej cechy jest dość jednorodna

• współczynnik wyższy od 65% oznacza bardzo silnie zróżnicowaną zbiorowość pod względem badanej cechy

• gdy wartość współczynnika zawiera się w granicach 35% - 65%, oznacza to, iż dane jednostki statystyczne w badanej zbiorowości są przeciętnie zróżnicowane

DANE Z PRZYKŁADU 1

DANE Z PRZYKŁADU 2

DANE Z PRZYKŁADU 3

Badane grupy robotników stanowią zbiorowości znacznie jednorodne pod względem wysokości płacy.

3. MIARY ASYMETRII

• pozwalają stwierdzić, czy przeważająca liczba jednostek statystycznych charakteryzuje się wartościami niższymi, czy wyższymi od przeciętnego poziomu badanej cechy

• gdy średnia arytmetyczna, mediana i dominanta są równe, mamy do czynienia z rozkładem symetrycznym

• gdy średnia arytmetyczna > mediana > dominanta, wówczas rozkład badanej cechy ma charakter asymetrii prawostronnej

• gdy średnia arytmetyczna < mediana < dominanta, wówczas rozkład badanej cechy ma charakter asymetrii lewostronnej

3.1. Bezwzględny wskaźnik asymetrii

• stanowi różnicę między średnia arytmetyczną a dominantą:

• gdy wskaźnik asymetrii = 0, wówczas mamy do czynienia z rozkładem symetrycznym, czyli taka sama liczba jednostek statystycznych charakteryzuje się wartościami niższymi oraz wyższymi od średniej arytmetycznej

• gdy wskaźnik asymetrii > 0, wówczas mamy do czynienia z asymetrią prawostronną, czyli dominująca liczba jednostek statystycznych charakteryzuje się wartościami badanej cechy niższymi od wartości przeciętnej

• gdy wskaźnik asymetrii < 0, wówczas mamy do czynienia z asymetrią lewostronną, czyli dominująca liczba jednostek statystycznych charakteryzuje się wartościami badanej cechy wyższymi od wartości przeciętnej

3.2. Względny wskaźnik asymetrii (współczynnik asymetrii)

• stanowi relację różnicy średniej arytmetycznej i dominanty do odchylenia standardowego:

• interpretacja współczynnika jest taka sama jak w przypadku bezwzględnego wskaźnika asymetrii

D=Me=

D Me

Me D

---