1. Metodyka całkowitych kosztów rocznych

Projektowanie elektroenergetycznych urządzeń zasilających czy to zakłady produkcyjne, czy to odbiorców prywatnych, powinno umożliwiać wybór pomiędzy rozwiązaniami równorzędnymi pod względem technicznym. Czynnikiem decydującym o wyborze staje się ocena ekonomiczna poszczególnych wariantów. Wybór najlepszego z punktu widzenia ekonomii rozwiązania oznacza wyselekcjonowanie projektu zapewniającego osiągnięcie zamierzonego celu: przesyłania, przetwarzania i zamiany energii elektrycznej na pracę przy jak najmniejszych kosztach. Obliczenia całkowitych kosztów rocznych stanowią podstawę rachunku gospodarczego stosowanego w elektroenergetyce, którego to zasady zostaną przedstawione w niniejszym opracowaniu.

2. Zasady obliczeń gospodarczych w elektroenergetyce

2.1 Ogólne zasady analizy ekonomicznej - rachunek dyskonta

Z gospodarczego punktu widzenia można wyróżnić dwa następujące etapy: budowy urządzenia, oraz jego eksploatacji. Z etapami tymi wiążą się ściśle dwa rodzaje nakładów finansowych:

1) nakłady inwestycyjne, czyli wydatki na budowę;

2) nakłady eksploatacyjne związane z użytkowaniem urządzenia.

Pierwsze z nich ponoszone są przed rozpoczęciem użytkowania i muszą być pokrywane z zasobów uzyskanych w jakiś inny sposób niż przychody będące wynikiem eksploatacji. Drugi rodzaj wydatków powstaje w okresie użytkowania urządzenia i pokrywany jest ze środków uzyskanych dzięki wykorzystywaniu obiektu. Po zakończeniu budowy w początkowej fazie eksploatacji konieczne jest pozyskanie środków na pokrycie bieżących kosztów użytkowania powstałych przed rozliczeniem za uzyskane efekty gospodarcze. Środki noszą nazwę środków obrotowych i są wydatkami jednorazowymi. Przy prawidłowej rotacji środków obrotowych, czyli przy małych zapasach magazynowych i szybkich rozliczeniach efektów użytkowych, wartość środków obrotowych w porównaniu z innymi kosztami jest bardzo mała a ich wpływ na obliczenia gospodarcze w elektroenergetyce, pomijalnie mały.

Wymienione wcześniej okresy: budowy i eksploatacji rozciągnięte są w czasie. Dlatego w celu obliczenia całkowitych poniesionych wydatków należałoby je zsumować. Tak uzyskana kwota nie może być podstawą oceny ekonomicznej, służącej jako kryterium optymalnego wyboru. Oczywiste jest, że różna powinna być ocena budowy takiego same obiektu, kosztującego np. milion złotych, jeżeli:

a) budowa trwa pięć lat a wydatki ponoszone są w następujący sposób: w pierwszym roku wydano 600 tys., a w następnych czterech latach po 100 tys.

b) budowa trwa dwa lata, a koszty inwestycyjne rozkładają się równomiernie w każdym roku po 500 tys.

W pierwszym przypadku na oczekiwane efekty finansowe należy czekać aż sześć lat, a w drugim tylko trzy. Ponieważ zyski uzyskiwane są tylko podczas użytkowania, a oczekiwanie na rozpoczęcie eksploatacji przy poniesionych wydatkach, powinno być z punktu widzenia ekonomii traktowane jako straty.

Dlatego też, niezbędne jest uwzględnienie w obliczeniach gospodarczych czynnika czasu, w tym, celu należy posłużyć się rachunkiem dyskonta. W czasie inwestowania i eksploatacji koszty ponoszone są na bieżąco, a w rachunku dyskonta zakłada się, że nakłady ponoszone są jednorazowo w ciągu roku, czyli koszty inwestycji występują jednorazowo na końcu roku inwestycji, a koszty eksploatacyjne na koniec roku eksploatacji.

W celu umożliwienia porównywania pod względem gospodarczym równorzędnych rozwiązań technicznych, zachodzi potrzeba przeliczenia wszelkich nakładów na wartość równoważną sprowadzoną do tzw. roku zerowego, czyli do roku poprzedzającego eksploatację.

Rozwój gospodarczy możliwy jest, gdy wartość środków, jakimi dysponujemy będzie cały czas wzrastać. Stosunek przyrostu (ΔE) środków w ciągu jednego roku, do wartości tych środków na początku roku (E) nazywamy stopą rozwoju lub stopą odpisu akumulacyjnego i oznaczamy symbolem p. W rachunku dyskonta wielkość ta nazywana jest stopą dyskontową.

Podstawową zależnością rachunku dyskonta [3] jest wyrażenie:

(2.1)

(2.2)

oznaczające, że wartość E po okresie N lat, przy stopie dyskonta p osiągnie wartość F. Na podstawie powyższych założeń i zależności dokonujemy sprowadzenia kosztów inwestycyjnych do wartości równoważnej w roku zerowym. Natomiast rozkład kosztów w czasie nazywamy charakterystyką czasową kosztów.

Załóżmy przykładową charakterystykę czasową kosztów:

Rok	-M	..-j..	-2	-1	0	1	2	..i..	N
Koszt inwest.	Kn(-M)	Kn(-j)	Kn(-2)	Kn(-1)	Kn(0)	Kn(1)	Kn(2)	Kn(i)	Kn(N)

Sprowadzając koszty inwestycyjne poniesione w poszczególnych latach do roku zerowego, otrzymamy, zgodnie z wzorami (2.1) i (2.2) wartości równoważne tych nakładów

(2.3)

Całkowite koszty inwestycyjne zdyskontowane na rok zerowy będą sumą nakładów ze wszystkich lat.

(2.4)

W przypadku, gdy nakłady inwestycyjne ponoszone są jedynie do roku zerowego i są każdego roku takie same, czyli K_n(-j) =const wtedy wzór (2.4) przybiera postać:

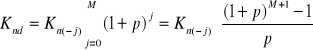
(2.5)

2.2 Metoda całkowitych kosztów rocznych

Koszty to wydatki pieniężne, jakie musimy ponieść w celu uzyskania określonych zasobów (najczęściej finansowych). Całkowite koszty roczne w elektroenergetyce to suma kosztów reprodukcji rozszerzonej i kosztów eksploatacyjnych.

(2.6)

gdzie: K_rr - koszty reprodukcji rozszerzonej,

K_e - koszty eksploatacyjne.

2.2.1 Koszty reprodukcji rozszerzonej

Koszty reprodukcji rozszerzonej stanowią sumę kosztów akumulacji K_ak i kosztów amortyzacji K_am [3].

(2.7)

Koszty akumulacji są to nakłady przeznaczane na rozwój środków produkcji i określone są zależnością:

(2.8)

gdzie: p - stopa dyskonta,

K_nd - nakłady inwestycyjne zdyskontowane na rok zerowy.

Czas akumulacji przyjmuje się dla stacji elektroenergetycznych najwyższych napięć na okres 35 lat, zaś dla stacji średnich napięć na okres 25 lat [1].

Koszty amortyzacji są częścią wartości obiektu, jaką trzeba odkładać, co roku, aby po okresie eksploatacji otrzymać równowartość obiektu na początku jego użytkowania. Czas amortyzacji przyjmujemy taki sam jak czas akumulacji. Poniższa zależność przedstawia sposób obliczania kosztów amortyzacji:

(2.9)

gdzie: a_r - stawka amortyzacji,

K_nd - nakłady inwestycyjne zdyskontowane na rok zerowy.

Zgodnie ze wzorem (2.1) wartość kosztów amortyzacji w N roku eksploatacji, czyli po N-1 latach użytkowania wyniesie:

(2.10)

Wartość kosztu amortyzacji w dowolnym roku eksploatacji wyniesie:

(2.11)

gdzie: i - dowolny rok,

czyli po N latach eksploatacji całkowita suma kosztów amortyzacji powinna być równa sumie nakładów inwestycyjnych zdyskontowanych na rok zerowy:

(2.12)

(2.13)

Wyrażenie
jest sumą ciągu geometrycznego o ilorazie
, dzięki czemu otrzymamy zależność:

(2.14)

Zależność (2.7) możemy przedstawić w postaci:

(2.15)

Wykorzystując zależność (2.14) otrzymamy następujący wzór określający wartość kosztów reprodukcji rozszerzonej:

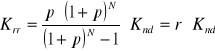
(2.16)

gdzie: r - współczynnik reprodukcji rozszerzonej.

2. Koszty eksploatacyjne

Koszty eksploatacyjne występują w czasie użytkowania obiektu i pokrywane są ze środków stanowiących efekt eksploatacji obiektu. Koszty eksploatacyjne można podzielić na dwie grupy:

a) koszty eksploatacyjne stałe K_es,

b) koszty eksploatacyjne zmienne K_ez.

Do pierwszej grupy zaliczamy koszty związane z remontami kapitalnymi i bieżącymi, zależne od kosztu urządzeń. Wyrażone są one jako części nakładów inwestycyjnych (bez dyskontowania). Następnym składnikiem tej grupy są koszty osobowe ruchu (tzw. robocizna), które są obliczone w zależności od liczby pracowników i średniego wynagrodzenia w ciągu roku. W obliczeniach gospodarczych można zastosować przybliżenie polegające na wyrażeniu tych kosztów jako proporcjonalnych do nakładów inwestycyjnych. Koszty administracyjne proporcjonalne do kosztów inwestycyjnych to następny składnik kosztów użytkowych stałych.

Tabela 2.1 Wskaźniki charakteryzujące koszty obiektów sieciowych [1].

Obiekt	Współczynniki kosztów eksploatacyjnych stałych [%]
		Remonty u	Ogólne o	Razem es
Urządzenia stacyjne (transformatory, rozdzielnie)	5	3,5	8,5

W powyższej tabeli koszty określone mianem „ogólne” oznaczają koszty osobowe ruch i koszty administracyjne.

Koszty eksploatacyjne stałe obliczane są wg zależności:

(2.17)

gdzie: K_n - nakłady inwestycyjne,

e_s - współczynnik kosztów eksploatacyjnych stałych.

Koszty eksploatacyjne zmienne K_ez związane są z obciążeniem stacji. Są to głównie straty mocy i energii. Określenie zmienne nie oznacza, że koszty te są różne każdego roku. Mogą być one jednakowe każdego roku przez cały okres eksploatacji, a „zmienność” ich oznacza zmiany związane ze sposobem eksploatacji i zmianami obciążenia stacji. Jeżeli składnik K_ez jest różny w poszczególnych latach eksploatacji (może to być spowodowane wzrostem obciążenia) to można zastąpić go równoważnym, czyli jednakowym każdego roku kosztem eksploatacyjnym zmiennym K_ezd. Dokonać tego możemy dyskontując te koszty wg następującej zależności:

(2.18)

gdzie: N - okres eksploatacji,

i - dowolny rok z okresu eksploatacji,

p - stopa dyskonta.

Koszty eksploatacyjne zmienne obliczamy z zależności [2]:

(2.19)

gdzie: ΔP - straty mocy,

ΔA - straty energii,

k_P - koszt jednostkowy strat mocy,

k_A - koszt jednostkowy strat energii,

τ - czas występowania strat maksymalnych.

Straty mocy są sumą strat mocy w transformatorze ΔP_t i dodatkowych strat mocy ΔP_d powstających na drodze przesyłu mocy biernej do transformatora.

Straty mocy w transformatorze ΔP_t obliczamy stosując wzór:

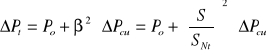
(2.20)

gdzie: P_o - jałowe straty mocy w transformatorze (wielkość katalogowa),

β - stopień obciążenia transformatora,

ΔP_cu - obciążeniowe straty mocy w transformatorze (wielkość

katalogowa).

Zainstalowanie transformatora, będącego odbiornikiem mocy biernej powoduje powstanie na drodze przepływu mocy biernej (od źródła do transformatora) dodatkowe straty mocy [2] czynnej ΔP_d.

(2.21)

gdzie: k_e - energetyczny równoważnik mocy biernej
,

Q_t - straty mocy biernej w transformatorze [kVar],

Q_o - jałowa strata mocy biernej [kVar],

Q_x - obciążeniowa strata mocy biernej przy obciążeniu

znamionowym,

i_o - prąd biegu jałowego [%] (wielkość katalogowa),

u_x - składowa bierna napięcia zwarcia [%],

S_Nt - moc znamionowa transformatora.

Składową bierną napięcia zwarcia można określić na podstawie: obciążeniowych strat mocy transformatora, mocy znamionowej transformatora, napięcia zwarcia.

(2.22)

(2.23)

gdzie: u_r - składowa czynna napięcia zwarcia,

u_z - napięcie zwarcia transformatora.

Energetyczny równoważnik mocy biernej k_e określa wpływ zmian wartości przesyłanej mocy biernej na wartość strat mocy czynnej.

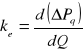
(2.24)

(2.24)

gdzie: ΔP_q - starty mocy czynnej wywołane przepływem mocy biernej,

Q - moc bierna obciążenia,

R - rezystancja jednej fazy.

Wartość równoważnika [2] będzie różna w poszczególnych punktach systemu elektroenergetycznego, zależnie od wartości przesyłanej mocy biernej i od odległości elektrycznej od źródła mocy. Wartości równoważnika przedstawione na poniższym rysunku można traktować jako przeciętne dla konkretnych obliczeń.

Straty energii obliczamy wykorzystując zależność:

(2.25)

lub po przekształceniach:

(2.26)

gdzie: τ - czas występowania strat maksymalnych [h],

T_r - czas włączenia transformatora do sieci [h].

Wielkość τ czyli czas trwania maksymalnych strat obciążeniowych została zdefiniowana wzorem:

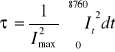
(2.27)

gdzie: I_max - największy prąd występujący w linii w danym roku,

I_t - wartość prądu w chwili t.

Obliczenie wartości τ z zależności (2.27) wymaga zarejestrowania przebiegu zmienności natężenia prądu w ciągu całego rozpatrywanego okresu, a więc praktycznie w ciągu całego roku. Jest to metoda niedogodna, jeżeli chodzi o obiekty znajdujące się w eksploatacji, a jest niemożliwa, jeżeli analizowane są obiekty będące w fazie projektowej (jak w naszym przypadku). Na podstawie danych z pomiarów zużytej energii oraz największego obciążenia można łatwo wyznaczyć czas użytkowania największego obciążenia T_s, który w jakiś sposób charakteryzuje przebieg obciążenia w czasie. Dlatego też powstało kilka wzorów określających zależność τ=f(T_s). Jednym z nich jest wzór Horaka [2]:

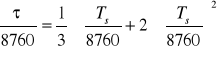
(2.28)

gdzie: τ - czas występowania maksymalnych strat obciążeniowych [h],

T_s - czas występowania maksymalnego obciążenia [h].

W pierwszym przybliżeniu możemy obliczać wartość τ jako:

(2.28)

Wzór Horaka odnosi się do warunków panujących w dużym systemie elektroenergetycznym. Przebiegi obciążenia u odbiorców różnią się od przebiegów obciążenia w systemie. Charakter przebiegu obciążenia u odbiorców przemysłowych uzależniony jest głównie od liczby zmian pracy. Z tego punktu widzenia należy odróżnić cztery kategorie odbiorców:

1) o ruchu ciągłym - roczny czas ruchu 8760[h],

2) o pracy trzyzmianowej - roczny czas ruchu 7000[h],

3) o pracy dwuzmianowej - roczny czas ruchu 4800[h],

4) o pracy jednozmianowej - roczny czas ruchu 2500[h].

U każdego z typów odbiorców zależność
należy interpretować inaczej. Służyć do tego mogą poniższe charakterystyki [3].

3. Koszty zawodności zasilania

Przerwy w dostawie energii mogą powodować powstawanie strat materialnych, dlatego też koszty zawodności zasilania możemy uwzględnić w rozszerzonej analizie kosztów całkowitych K_c.

(2.29)

gdzie: K_c - koszty całkowite,

K_cr - całkowite koszty roczne,

K_zi - koszty zawodności zasilania.

Koszty strat K_zi powodowane przerwami w dostawie energii elektrycznej w czasie t dają się określić zależnością [1]:

(2.30)

gdzie: W_rn - wartość rynkowa nie wykonanej produkcji,

K_m - koszty nie zużytych materiałów,

K_e - koszty nie zużytej energii,

K_d - koszty strat dodatkowych związanych z postojami.

Bardzo trudne do oszacowania są koszty dodatkowe, zmieniające się nieliniowo w czasie. Składają się na nie koszty spowodowane:

- zniszczeniem surowców i materiałów,

- naprawą lub wymianą zniszczonych maszyn i urządzeń,

- stratami wynikającymi z pogorszenia jakości wyrobów po wznowieniu

produkcji,

- stratami pośrednimi w zakładach wykorzystujących produkty

analizowanego zakładu.

Charakterystyki czasowe strat występują w następującej formie:

- liniowa o równaniu:

(2.30)

- nieliniowa aproksymowana odcinkami linii prostych o równaniach jak zależność (2.30).

Przedstawione zależności dotyczą procesów ciągłych o stałej w czasie intensywności produkcji, dla których chwila wystąpienia przerwy w zasilaniu nie wpływa na wartość strat. W rzeczywistości jednak występuje wiele zakładów produkcyjnych, w których intensywność wytwarzania zależy od pory dnia, a ponadto każda chwila odpowiada innej intensywności produkcji. Wynika więc z tego, iż koszty strat w tym samym zakładzie mogą być bardzo różne i trudne do oszacowania w fazie projektowej.

Skutki przerw w dostawach energii dla odbiorców komunalnych są wyjątkowo trudne do obliczenia lub nawet niemożliwe do oszacowania, ponieważ przy przerwach występujących w czasie pobytu mieszkańców w domu następuje wymuszona utrata lub bardzo silne ograniczenie ich aktywności, polegające na niemożliwości: przygotowywania posiłków, sprzątania, nauki, czy wykonywania dodatkowej pracy zawodowej.

Przeprowadzenie rozszerzonych obliczeń gospodarczych wydaje się celowe dla zakładów już istniejących i produkujących, ponieważ tylko dla nich możemy określić koszty dodatkowe, będące składnikiem kosztów zawodności zasilania.

3. Przykładowe obliczenia

3.1 Przykład 1

A. Dane wejściowe:

Transformatory:
Liczba transformatorów		2
	Transformator typ 1			Transformatory typ 2
Typ:	TONa 2000/30			TONa 1000/30
Liczba sztuk	1			1
Moc znamionowa Sn	2000 [kVA]			1000 [kVA]
Napięcie górne GN	31500 [V]			31500 [V]
Napięcie dolne DN	6300V			6300V
Napięcie zwarcia uz%	6%			6%
Straty jałowe ΔPo	3100 [W]			3100 [W]
Straty obciążeniowe ΔPcu	17000 [W]			17000 [W]
Prąd jałowy Io	0,8 [%]			1 [%]
Dane inwestycyjne:
Suma nakładów inwestycyjnych			6240000 zł.
Okres inwestowania			3 lata
Okres eksploatacji			30 lat
Stopa dyskontowania			0,08
Dane eksploatacyjne:
Stopień obciążenia β	Transformator 1			Transformatory 2
	0,85			0,85
Czas włączenia stacji do sieci T			2250 [h]
Czas użytkowania mocy szczytowej			2125 [h]
Energetyczny równoważnik mocy biernej ke			0,19

B. Obliczenia

Nakłady inwestycyjne są rozłożone równomiernie w okresie inwestycji oznaczana to, że w jednym roku inwestycji koszty wynoszą 2080000 zł.

1. Nakłady inwestycyjne zdyskontowane na rok zero wynoszą:

=2426112+2246400+208000=6752512zł.

2. Koszty akumulacji:

= 0,08*6752512 ≅ 540201 zł.

3.Koszty amortyzacji:

59607 zł.

4. Koszty reprodukcji rozszerzonej:

599808 zł.

5. Koszty eksploatacyjne stałe;

≅ 573964 zł.

6. Koszty eksploatacyjne zmienne:

6.1 Straty mocy w transformatorach:

dla TONa 2000/30
= 15,3825 [kW],

dla TAOo 1000/30
= 10,192 [kW],

6.2 Straty mocy powstałe na drodze przesyłu:

dla TONa 2000/30
=19,348 [kW],

dla TAOo 1000/30
= 9,605 [kW],

6.3 Suma strat mocy:

= 54,9125 [kW]

7. Straty energii:

dla TONa 2000/30
= 64970,76 [kWh],

dla TAOo 1000/30
= 38604,27 [kWh]

Suma strat energii:

= 103575,03 [kWh]

8. Koszty strat:

mocy = 10707,9375 zł,

energii = 29104,58343 zł.

9. Suma kosztów eksploatacyjnych:

= 39812,52 +573964 zł = 613776,52 zł.

10. Całkowite koszty roczne ≅ 1213584,52 zł.

D. Zestawienie.

Wyszczególnienie	Wynik obliczeń
Koszty akumulacji:	540201[zł.]
Koszty amortyzacji	59607[zł.]
Koszty reprodukcji rozszerzonej	599808[zł.]
Koszty eksploatacyjne stałe	573964[zł.]
Suma strat mocy	54,9125 [kW]
Suma strat energii	103575,03 [kWh]
Koszty eksploatacyjne zmienne	39812,52 [zł.]
Całkowite koszty roczne	1213584,52 zł

3.2 Przykład 2

A. Dane wejściowe:

Transformatory:
Liczba transformatorów			3
	Transformator typ 1				Transformatory typ 2
Typ:	TOd 630/15				TOd 400/15
Liczba sztuk	2				1
Moc znamionowa Sn	630 [kVA]				400 [kVA]
Napięcie górne GN	15750 [V]				15750 [V]
Napięcie dolne DN	400V				400V
Napięcie zwarcia uz%	6%				4,5%
Straty jałowe ΔPo	800 [W]				610 [W]
Straty obciążeniowe ΔPcu	6750 [W]				4600 [W]
Prąd jałowy Io	1,2 [%]				1,2 [%]
Dane inwestycyjne:
Suma nakładów inwestycyjnych				3448776 zł.
Okres inwestowania				3 lata
Okres eksploatacji				50 lat
Stopa dyskontowania				0,08
Dane eksploatacyjne:
Stopień obciążenia β		Transformator typ 1				Transformatory typ 2
		0,85				0,7
Czas włączenia stacji do sieci T				2250 [h]
Czas użytkowania mocy szczytowej				2000 [h]
Energetyczny równoważnik mocy biernej ke				0,15

B. Obliczenia „ręczne”

Nakłady inwestycyjne są rozłożone równomiernie w okresie inwestycji oznaczana, czyli w każdym z trzech lat inwestycji są jednakowe i wynoszą149592 zł.

1. Nakłady inwestycyjne zdyskontowane na rok zero wynoszą:

=1340884,12+1241559,36+1149592=3732035,5zł.

2. Koszty akumulacji:

= 0,08*3448776 ≅ 298562,824 zł.

3.Koszty amortyzacji:

6505 zł.

4. Koszty reprodukcji rozszerzonej:

305067,824 zł.

5. Koszty eksploatacyjne stałe;

≅ 298562,824 zł

6. Koszty eksploatacyjne zmienne:

6.1 Straty mocy w transformatorach:

dla TOd 630/15
= 5,6769 [kW],

dla TOd 400/15
= 2,864 [kW],

6.2 Straty mocy powstałe na drodze przesyłu:

dla TONa 2000/30
=5,1623 [kW],

dla TAOo 1000/30
= 1,9992 [kW],

6.3 Suma strat mocy:

= 26,5416 [kW]

7. Straty energii:

dla TOd 620/15
= 19926,14 [kWh],

dla TOd 400/15
= 8754,11 [kWh]

Suma strat energii:

= 48606,39 [kWh].

8. Koszty strat:

mocy = 5175,61 zł,

energii = 13658,4 zł.

9. Suma kosztów eksploatacyjnych:

= 298562,824 +18834,01 zł =317396,834 zł.

10. Całkowite koszty roczne ≅ 622464,658 zł.

D. Zestawienie.

Wyszczególnienie	Wynik obliczeń
Koszty akumulacji:	298562,824 [zł]
Koszty amortyzacji	6505[zł]
Koszty reprodukcji rozszerzonej	305067,824[zł]
Koszty eksploatacyjne stałe	298562,824[zł]
Suma strat mocy	26,5416[kW]
Suma strat energii	97212,78[kWh]
Koszty eksploatacyjne zmienne	18834,01 [zł]
Całkowite koszty roczne	622464,658 [zł]

4. Wniosek

Obliczenia całkowitych kosztów rocznych dla różnych rozwiązań techniczno-inwestycyjnych pomagają w wyborze rozwiązania przynoszącego najmniejsze koszty, czyli z ekonomicznego punktu widzenia, dającego największe zyski.

5. Literatura

[1] Bełdowski T., Markiewicz H.: Stacje i urządzenia elektroenergetyczne. Warszawa WNT 1998.

[2] Bartodziej G.: Dobór urządzeń rozdzielczych wysokiego napięcia. Gliwice Wydawnictwo Politechniki Śląskiej 1975.

[3] Gosztowt W.: Gospodarka elektroenergetyczna w przemyśle. Warszawa WNT 1971.

Obliczenia gospodarcze w elektroenergetyce

Strona 1

Rys 2.1 Wartość energetycznego równoważnika mocy w punktach układu elektroenergetycznego.

W liczniku wartość dla największego, a w mianownika dla najmniejszego obciążenia mocą bierną.

Rys 2.2 Zależność

dla odbiorców o ruchu ciągłym.

Rys 2.3 Zależność

dla odbiorców o pracy trzyzmianowej

Rys 2.4 Zależność

dla odbiorców o pracy dwuzmianowej

Rys 2.5 Charakterystyki czasowe strat powodowanych

zawodnością zasilania:

1 - liniowa (b=0),

2 - liniowa (b>0),

3 - nieliniowa aproksym.

Odcinkami prostych

t_a - czasy krytyczne przerw

w zasilaniu.

1

2

3

---