Rok akademicki 2006/2007	Laboratorium z fizyki
Nr ćwiczenia 62	Zależność oporności ciał stałych od temperatury
Wydział : WBiŚ Kierunek : IŚ OCiK, lab.3	Hanna Spierewka
Data	Ocena		Data zaliczenia	Podpis
21.11.2006r.	T
		S

1. Zasada pomiaru

Celem ćwiczenia było poznanie teorii przewodnictwa elektrycznego ciał stałych, sprawdzenie eksperymentalnych zależności oporności właściwej od temperatury dla metali, półprzewodników i konstantanu.

Oporność właściwa metali rośnie proporcjonalnie do temperatury - wynika to z zastosowania klasycznej teorii elektronowej przewodnictwa, w myśl której rosnąca temperatura powoduje wzrost drgań sieci krystalicznej, a tym samym wzrost prawdopodobieństwa zderzenia się nośnika prądu (elektronu) z atomem sieci, czyli skrócenie drogi swobodnej elektronów.

Do opisu właściwości połprzewodników lepiej nadaje się teoria pasmowa, zgodnie z którą rosnąca temperatura powoduje wzrost liczby swobodnych nośników, a tym samym zwiększenie przewodności ze wzrostem temperatury.

Konstantan natomiast jest mniej ciekawym, choć może bardziej intrygującym z badawczego punktu widzenia stopem wieloskładnikowym zawierającym Cu, Ni, Mn, Fe i C, odznaczającym się dużym oporem właściwym i małym współczynnikiem temperaturowym oporu oznacza to, że w szerokim zakresie temperatur nic się nie dzieje.

Jak wynika z klasycznej teorii elektronowej (przydatnej w opisie metali) oporność właściwa metali zwiększa się proporcjonalnie do temperatury. W myśl jej wzrost temperatury w metalu powoduje wzrost drgań sieci krystalicznej, a tym samym zwiększenie prawdopodobieństwa zderzenia się nośników prądu (jakimi są elektrony) z atomem sieci, czyli skrócenie ich drogi swobodnego poruszania.

Jednym z praw, wywodzących się od klasycznej teorii elektronowej, jest tzw. prawo Wiedemanna-Franza, które mówi, że:

„Stosunek współczynnika przewodnictwa cieplnego metalu λ do współczynnika      przewodnictwa właściwego σ jest jednakowy dla wszystkich metali i proporcjonalny do      temperatury”, tzn.:

gdzie: L - współczynnik wyznaczony eksperymentalnie (tzw. liczba Lorentza)

Otrzymana eksperymentalnie zależność ρ = f (T) pozwala wyznaczyć współczynnik temperaturowy zmiany oporności właściwej metalu:

Do opisu właściwości półprzewodników lepiej nadaje się tzw. teoria pasmowa, zgodnie z którą wzrostowi temperatury towarzyszy wzrost liczby swobodnych nośników. Jest to wynikiem „przeskoku” elektronów z pasma podstawowego do pasma przewodnictwa. Tym samym zwiększa się przewodność w półprzewodniku.

W przypadku półprzewodników samoistnych ich przewodnictwo jest funkcją ruchliwości odpowiednich nośników:

gdzie: μ_n - ruchliwość elektronów

μ_p - ruchliwość dziur

n - koncentracja elektronów

p - koncentracja dziur

2. Schemat układu pomiarowego

3. Ocena dokładności pojedynczych pomiarów

ΔR = ± 1% wartości odczytu + czułość

ΔT = 0,5 °C

4. Tabele pomiarowe

Lp.	T	german		miedź		konstantan
	[°C]	R [kΩ]	ΔR [kΩ]	R [kΩ]	ΔR [kΩ]	R [kΩ]	ΔR [kΩ]
1	25	0,447	0,0045	0,271	0,0027	0,177	0,0018
2	30	0,426	0,0043	0,275	0,0027	0,178	0,0018
3	35	0,377	0,0038	0,279	0,0028	0,194	0,0019
4	40	0,423	0,0042	0,298	0,0030	0,192	0,0019
5	45	0,298	0,0030	0,288	0,0029	0,180	0,0018
6	50	0,255	0,0025	0,292	0,0029	0,179	0,0018
7	55	0,214	0,0021	0,299	0,0030	0,179	0,0018
8	60	0,189	0,0019	0,301	0,0030	0,178	0,0018
9	65	0,180	0,0018	0,303	0,0030	0,178	0,0018
10	70	0,150	0,0015	0,312	0,0031	0,177	0,0018
11	75	0,140	0,0014	0,309	0,0031	0,176	0,0018
12	80	0,118	0,0012	0,314	0,0031	0,176	0,0018
13	85	0,107	0,0011	0,318	0,0032	0,176	0,0018
14	90	0,089	0,0009	0,323	0,0032	0,176	0,0018
15	95	0,078	0,0008	0,329	0,0033	0,176	0,0018
16	100	0.067	0,0007	0,334	0,0033	0,176	0,0018

Wyniki obliczeń temperatury i logarytmu oporu elektrycznego germanu.

Lp.	I [A]	t [°C]	T [K]	1/T [1/K]	German
										R	lnR
										[kΩ]
1	0,7	25	298	0,0034	0,447	-0,80
2	0,7	30	303	0,0033	0,426	-0,85
3	0,7	35	308	0,0032	0,377	-0,97
4	0,7	40	313	0,0032	0,423	-0,86
5	0,7	45	318	0,0031	0,298	-1,22
6	0,7	50	323	0,0031	0,255	-1,37
7	0,7	55	328	0,0030	0,214	-1,54
8	0,7	60	333	0,0030	0,189	-1,67
9	0,7	65	338	0,0029	0,180	-1,71
10	0,7	70	343	0,0029	0,150	-1,90
11	0,7	75	348	0,0029	0,140	-1,97
12	0,7	80	353	0,0028	0,118	-2,14
13	0,7	85	358	0,0028	0,107	-2,23
14	0,7	90	363	0,0027	0,089	-2,42
15	0,7	95	368	0,0027	0,078	-2,55
16	0,7	100	373	0,0027	0,067	-2,70

5. Przykładowe obliczenia wyniku pomiaru

Metal - miedź

Na podstawie wykresu możemy stwierdzić, że ze wzrostem temperatury rezystancja metali rośnie i charakter tego wzrostu jest liniowy. Tylko w bardo niskich temperaturach wzrost ten jest nieliniowy.

Wartość współczynnika temperaturowego oporu:

Półprzewodnik - german

Zależność lnR = f(1/T) jest liniowa. Możemy obliczyć wartość współczynnika B, który jest współczynnikiem kierunkowym tej prostej.

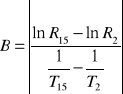
Stała materiałowa B jest właściwie energią aktywacji półprzewodnika znormalizowaną przez czynnik 2k (k - stała Boltzmana) i wyraża się wzorem:

Można więc na jej podstawie bezpośrednio wyznaczyć energię aktywacji:

1 [eV] = 1,602·10^-19 [J]

Znając stałą B można obliczyć współczynnik temperaturowy dla półprzewodnika:

Lp.		T[K]
1	- 0,032	298
2	- 0,031	303
3	- 0,030	308
4	- 0,029	313
5	- 0,028	318
6	- 0,027	323
7	- 0,026	328
8	- 0,025	333
9	- 0,025	338
10	- 0,024	343
11	- 0,023	348
12	- 0,023	353
13	- 0,022	358
14	- 0,021	363
15	- 0,021	368
16	- 0,020	373

6. Rachunek błędów

Błędy pomiaru oporów R materiałów:

Np. dla germanu nr 3:

R₃ = 0,377 [kΩ] ΔR = 1% · 0,377 = 0,0038 [kΩ]

7. Zestawienie wyników pomiarów

Temperaturowe współczynniki zmian oporu:

- dla metalu (miedzi) - α_m = 0,0031 [1/K]

- dla półprzewodnika (germanu) - α_p :

Lp.		T[K]
1	- 0,032	298
2	- 0,031	303
3	- 0,030	308
4	- 0,029	313
5	- 0,028	318
6	- 0,027	323
7	- 0,026	328
8	- 0,025	333
9	- 0,025	338
10	- 0,024	343
11	- 0,023	348
12	- 0,023	353
13	- 0,022	358
14	- 0,021	363
15	- 0,021	368
16	- 0,020	373

Energia aktywacji E_g = 0,49 [eV]

Stała materiałowa B = 2833,33 [K]

8. Uwagi i wnioski

Wyniki doświadczenia potwierdziły liniową zależność oporności właściwej metalu od temperatury oraz stabilność tej wielkości w szerokim zakresie temperatur dla konstantanu. Obliczona wartość energii aktywacji germanu wyniosła 0,49 eV.

---