POLITECHNIKA WROCŁAWSKA WROCŁAW, 20.01.2000

WYDZIAŁ GÓRNICZY

ROK V, EOP

REFERAT

ZASTOSOWANIE WSPÓŁCZYNNIKA PRZEJMOWANIA CIEPŁA W WYROBISKACH GÓRNICZYCH

WYKONAŁ:

TOMASZ ŚLĘZAK

W zagadnieniach związanych z regulacją warunków klimatycznych w wyrobiskach górniczych zasadniczą rolę odgrywa wymiana ciepła między przepływającym powietrzem i otaczającym górotworem.

W większości prac dotyczących prognozy temperatury powietrza przyjmuje się, że wymiana ciepła między górotworem a powietrzem zachodzi na drodze konwekcji opisanej równaniem Newtona:

q = α × Δt × A (1)

q - ilość ciepła, [W]

α - współczynnik wymiany ciepła, [W/m²K]

Δt - różnica temperatur ośrodków wymieniających ciepło. [K]

A - powierzchnia wymiany, [m²]

Analogicznie ilość wymienionej wilgoci opisuje zależność:

m_w = k × ΔΠ × A (2)

gdzie:

k - współczynnik wymiany wilgoci, [s/m]

ΔΠ-siła napędowa wymiany wilgoci, [Pa]

Siłę napędową przy wymianie wilgoci może być różnica ciśnień pary wodnej w warstwie granicznej Δp, różnica wilgotności właściwych Δx, różnica wilgotności względnej Δϕ czy różnica potencjałów Δ c.

Z tego względu współczynnik wymiany wilgoci k może być różnie określany. Jednakże istnieje dosyć silny związek między tymi współczynnikami niezależnie od użytej siły napędowej.

Istnieje także w określonych warunkach związek między współczynnikiem wnikania ciepła i wilgoci określony przez Lewisa:

ϕ = a/D = α/ β (3)

gdzie:

a - współczynnik wyrównania temperatury w powietrzu, [m²/s]

D - współczynnik dyfuzji pary wodnej w powietrzu, [m²/s]

β - współczynnik przejmowania masy, [m/s]

znając współczynnik przejmowania wilgoci β, ilość wymienionej wilgoci oblicza się z zależności:

(4)

gdzie:

R_w - stała gazowa pary wodnej, [J/kgK]

T - temperatura powietrza, [°K]

Podobne związki można znaleźć między współczynnikami wnikania ciepła i wilgoci przy stosowaniu siły napędowej Δx czy Δϕ.

Dokładność ilości ciepła, wg zależności (1) uzależniona jest od dokładności zastosowanego współczynnika wnikania ciepła.

W pracach dotyczących wymiany ciepła, współczynnik wnikania ciepła oblicza się z ogólnej zależności uzyskanej na drodze badań empirycznych:

Nu = A × Re^B × Pr^C (5)

Gdzie:

- liczba Nusselta,

- liczba Reynoldsa

- liczba Prandla

d - średnica hydrauliczna przewodu, [m.]

w - prędkość powietrza, [m/s]

l - współczynnik przewodnictwa cieplnego powietrza, [W/mK]

ν - współczynnik lepkości kinematycznej powietrza, [m²/s]

c_p - ciepło właściwe powietrza, [J/kgK]

η - współczynnik lepkości dynamicznej powietrza, [kg/ms]

Jeżeli zachodzi równoczesna wymiana ciepła i masy to przy tych samych wartościach liczby Re zmienia się grubość warstwy przyściennej w zależności od intensywności parowania. Zależność na określenie współczynnika α przyjmuje wtedy postać:

Nu = A × Re^B × Pr^C ×Gu^D (6)

gdzie:

- liczba Guchmana

t_s - temperatura powietrza mierzona termometrem suchym, [°C]

t_w - temperatura powietrza mierzona termometrem wilgotnym, [°C]

Wyznaczenie stałej A oraz wykładników potęgowych B,C i D zajmowali się między innymi: Nusselt, Guchman, Mc Adams, Michiejew, Fiodorow, Sergeew, Niestierenko i inni.

W tablicy 1 podano wartości A,B,C,D w odniesieniu do wymiany ciepła i masy.

Z tablicy wynika, że większość badań obejmuje zakres liczby R_e < 3 10⁵ , oraz wymiany ciepła bez równoczesnej wymiany masy w rurach gładkich. Celem uwzględnienia chropowatości ścian wyrobiska, Szczerbań przeprowadził badania, uwzględniając różną chropowatość oraz obudowę. Badania wykazały, że wzrost chropowatości ścian powoduje wzrost współczynnika wnikania ciepła 1-3 razy.

Tablica 1. Porównanie parametrów empirycznych stosowanych w zależnościach do obliczania współczynników wymiany ciepła i wilgoci.

Lp.	Zakres liczby Re	Wnikanie ciepła			Wnikanie masy			Autor	Rodzaj badań
		A	B	C	A	B	C
1	3,1 + 22 10^3	0,51	0,61	0,17	0,49	0,61	0,13	Niestierenko
2	2,2 + 31 10^4	0,027	0,9	0,17	0,025	0,9	0,13	Niestierenko
3	1+ 500 10^4	0,021	0,8	-	-	-	-	Michiejewa	Rury gładkie
4	1 + 20 10^4	0,023	0,8	-	-	-	-	Mc Adams	Rury gładkie
5	1 - 13 10^4	0,45	0,58	-	-	-	-	Stukało	Węgiel w wozach
6	1 - 13 10^4	0,028	0,8	-	-	-	-	Stukało	Węgiel w przenośnikach.
7	1 - 10 10^4	0,042	0,8	-	-	-	-	Szczerban	Wyrobiska górn.-model
8	1 - 10 10^4	0,024	0,8	-0,16	76 10^-5	0,8	-0,48	Fiodorow	Suszenie cegły
9		0,06	0,8	0,09	0,096	0,75	0,13	Sergeew	Parowanie wody z pow. kap
10	1 - 50 10^5	4,5 10^-4	0,9	-0,5	4,3 10^-4	0,90	-0,5	Frączek	Wyrobiska górnicze

W wyrobiskach zawilgoconych celem obliczania współczynnika wnikania Voss i Szczerbań proponują stosować współczynnik będący sumą współczynnika wnikania ciepła na drodze konwekcji α_{k i} parowania α_p .

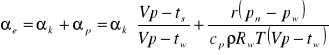
(7)

gdzie:

Vp - temperatura powierzchni wyrobiska, [°C]

t_s - temperatura powietrza, [°C]

t_w - temperatura wilgotna powietrza, [°C]

r - ciepło parowania wody, [kJ/kg]

p_n - ciśnienie pary wodnej na powierzchni wyrobiska, [Pa]

p_w - ciśnienie pary wodnej w powietrzu, [Pa]

c_p - ciepło właściwe powietrza, [kJ/kgK]

ρ - gęstość powietrza, kg/m³

R_w - stała gazowa pary wodnej, [kJ/kgK]

T - temperatura bezwzględna powietrza, [°K]

Zastosowanie wzoru (7) powoduje wzrost współczynnika wnikania ciepła 2÷3 razy. Nie uwzględnia jednak wilgoci, która bezpośrednia dyfunduje z górotworu.

W celu uwzględnienia wpływu wymiany wilgoci na wymianę ciepła zostanie empirycznie określony współczynnik wymiany wilgoci.

W wyrobiskach górniczych wydrążonych w skałach zawierających wilgoć, nawilżenie powietrza następuje równocześnie z dwóch źródeł:

• Bezpośrednio z górotworu pary wodnej powstałej w procesie parowania i desorpcji wewnątrz górotworu,

• Pary powstałej w procesie powierzchniowego parowania,

Z prowadzonych badań w zakresie ruchu wilgoci w wyrobiskach górniczych wynika, że:

• Nawilżanie powietrza następuje nie tylko w wyrobiskach wilgotnych, ale także w wyrobiskach kompletnie suchych,

• Strumień wilgoci nawilżający powietrze zmniejsza się wraz ze wzrostem czasu,

• Duży wpływ na wilgotność powietrza ma woda używana podczas urabiania i transportu urobku,

• Wzrost głębokości eksploatacji powoduje wzrost zawilżenia powietrza,

Poczyniono obserwacje pozwoliły autorowi wysunąć przypuszczenia, że dotychczasowy sposób ujęcia ruchu wilgoci w wyrobiskach górniczych w postaci ogólnej funkcji:

M_w = f(Δp, A, R_w, T, R_e, P_r) (8)

Jest niepełny. W celu ruchu wilgoci wewnątrz górotworu należałoby uwzględnić ciśnienie pary w stanie pierwotnym oraz zawartości wilgoci wolnej w górotworze. Ponadto znaczny wpływ na ruch wilgoci w górotworze ma ciśnienie górotworu oraz wytrzymałość mechaniczna na ściskanie skał wokół wyrobiska (σ_g). W skałach o większej wytrzymałości na ściskanie stwierdza się większy ruch wilgoci. Uwzględniając także czynniki zawarte w zależności (7) można napisać, że strumień wilgoci nawilżający powietrze opisze zależność:

M_w = f (Δp, A, R_w, T, R_e, P_r, ν, t_w, Δz, σ_g, ρ_g, τ,a_g, ρ_w ) (9)

Gdzie:

ν - temperatura pierwotna górotworu, [°C]

Δz - głębokość zalegania wyrobiska, [m.]

σ_g - współczynnik wytrzymałości mechanicznej skał na ściskanie, [Pa]

ρ_g - gęstość górotworu, [kg\m³]

τ - okres istnienia wyrobiska, [s]

a_g - współczynnik wyrównania temperatury w skałach, m²/s

ρ_w - gęstość przestrzenna wody w górotworze, kg/m³

Współczynnik dyfuzji pary wodnej z powierzchni wyrobiska do powietrza będzie o wiele większy od współczynnika dyfuzji pary wewnątrz górotworu, natomiast nie zawsze cała powierzchnia wyrobiska będzie pokryta wodą.

Celem uproszczenia modelu fizycznego wymiany wilgoci przyjęto, że nieznana wartości w zależności (4) stanowią:

• Powierzchnia (A) pokryta wodą,

• Wypadkowy współczynnik przejmowania wilgoci

Stosując metodę podobieństwa (4,5,6) ustalono liczby bezwymiarowe opisujące ruch wilgoci w wyrobisku górniczym w postaci:

Sh_w = A, R_e^B, Pr^C,Gu^D,R^E,K^F,Fo^G,W^H

Gdzie:

R = Δz × ρ_g /σ_g - liczba podobieństwa wytrzymałościowego górotworu,

K = t_s -ν/t_s+273 - liczba podobieństwa temperaturowego

Fo = a × τ /r^{2 -} Liczba Fouriera,

W = ρ_w / ρ_g - liczba podobieństwa wilgotności górotworu

Celem wyznaczenia wykładników potęgowych B,C,D,E,F,G,H, przeprowadzono niezbędne pomiary w 360 wyrobiskach górniczych 20 kopalń Górnośląskiego Zagłębia Węglowego. Wyrobiska górnicze ze względu na przeznaczenie sklasyfikowano w czterech grupach:

• szyby,

• wyrobiska kamienne,

• wyrobiska węglowe,

• ściany.

Stosując metodę najmniejszych kwadratów ustalono wykładniki potęgowe zależności (10) dla wyrobisk w poszczególnych grupach wyrobisk. Okazało się, że np. wykładnik liczby Re przyjmie najwyższe wartości B=1,6 w szybach a najmniejsze B= 0,25 w wyrobiskach węglowych. Natomiast wykładnik liczby Gu przyjmował najmniejsze wartości w szybach a największe w ścianach. Ponadto stwierdzono niewielki wpływ liczby Fo w danej grupie wyrobisk. Mając to na uwadze wykonano powtórne obliczenia już nie w poszczególnych grupach wyrobisk, lecz w całości. Następnie przeprowadzono rozdział całkowitego strumienia wilgoci, na strumień wilgoci odparowującej z powierzchni oraz wewnątrz górotworu m_g. Statystycznemu opracowaniu poddano funkcję typu:

Sh_w = Sh_p + Sh_g = A_g R^0,9 Gu^-0,5 + A₂ R^-0,7 K^0,6 W^-0,3 (11)

Okazało się jednak, że na strumień wilgoci płynący z górotworu ma także wpływ liczba Re. Ostatecznie ustalono postać funkcji:

Sh_w = Re^{0,9 (}A₁ Gu^-0,5 + A₂ R^-0,7 K^0,6 W^-0,3 (12)

Ostatecznie uzyskano następujące zależności w poszczególnych grupach wyrobisk;

Ścian

Sh_w = 10^-3 Re^0,9 Gu^-0,5 + 3,3 10^-4 Re^0,9 w^-0,3 R^-0,7 K^0,6 (13)

Wyrobiska węglowe

Sh_w = 4,7 10^-4 Re^0,9 Gu^-0,5 + 1,9 10^-4 Re^0,9 w^-0,3 R^-0,7 K^0,6 (14)

Wyrobiska kamienne

Sh_w = 0,72 10^-4 Re^0,9 Gu^-0,5 + 1,5 10^-4 Re^0,9 w^-0,3 R^-0,7 K^0,6 (15)

Szyby

Sh_w = 1,3 10^-3 Re^0,9 Gu^-0,5 K^0,6 (16)

Podane wzory uzyskano dla warunku ν > t_s. Ponieważ w szybach w okresie letnim mamy doczynienia z warunkiem ν < t_s wtedy zależność do obliczenia β ma postać:

Sh_w = 6 10^-6 Re^0,9 Gu^-0,5 K-^0,6 (17)

Korzystając z zależności (13-17) można ustalić zależność opisującą wymianę ciepła w wyrobiskach górniczych. W tym celu wykorzystujemy pierwszy składnik:

Nu = A Re^0,9 Gu^-0,5

Wartość stałej A proponuje się przyjąć A = 5 *10^-4 dla wyrobisk węglowych kamiennych i szybów oraz

A = 10* 10^-4 dla ścian. przyjmując ponadto średnią wartość liczby Gu = 0,005 uzyskamy zależność na obliczanie współczynnika wnikania ciepła w wyrobiskach węglowych:

Oraz w ścianach

Powyższe zależności ujmując wpływ wymiany wilgoci, pozwalają dokładniej obliczyć wymianę ciepła w wyrobisku niż zależności (5-7).

---