ZAJĘCIA NR 4

PRAWDOPODOBIEŃSTWO ROZKŁADU:

określenie normy

odrzucanie wyników

ROZKŁAD NORMALNY:

ROZKŁAD PRAWDOPODOBIEŃSTW:

• rzut JEDNĄ monetą:

2 możliwości

jednakowe prawdopodobieństwo = ½

orzeł (O) reszka (R)

• rzut DWOMA monetami:

4 możliwości OO OR RO RR

P_O = 0,25 P_O = 0,5 P_O = 0,25

P_R = 0,25 P_R = 0,5 P_R = 0,25

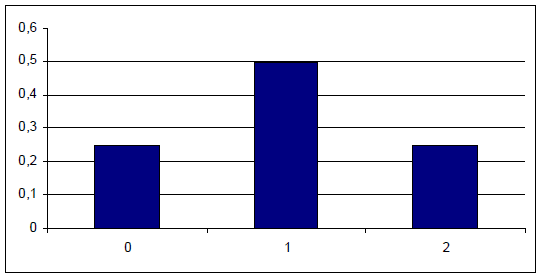
• rzut TRZEMA monetami:

8 możliwości OOO OOR ORO ROO

ROR RRO ORR RRR

liczba orłów/ reszek: prawdopodobieństwo:

0 ¹/₈ 0,125

1 ³/₈ 0,375

2 ³/₈ 0,375

3 ¹/₈ 0,125

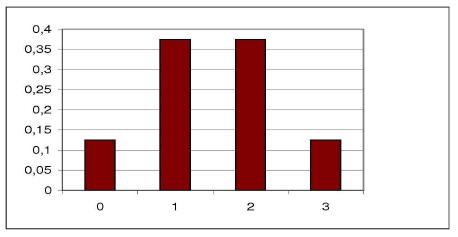
• rzut CZTEREMA monetami:

16 możliwości OOOO

OOOR OORO OROO ROOO

OORR ORRO RROO ROOR RORO OROR

ORRR RRRO RORR RROR

RRRR

liczba orłów/ reszek: prawdopodobieństwo:

0 ¹/₁₆ 0,0625

1 ⁴/₁₆ 0,25

2 ⁶/₁₆ 0,375

3 ⁴/₁₆ 0,25

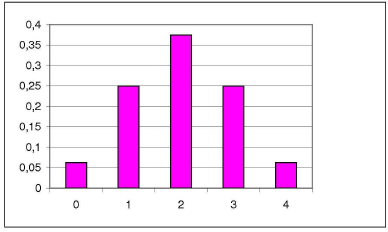
4 ¹/₁₆ 0,0625

Sposoby ustalania rozkładu prawdopodobieństw

uzyskania odpowiedniej liczby orłów i reszek:

empirycznie teoretycznie

rzucanie monetą ROZKŁAD DWUMIANOWY:

p = prawdopodobieństwo uzyskania orła w jednej próbie

q = prawdopodobieństwo uzyskania reszki w jednej próbie

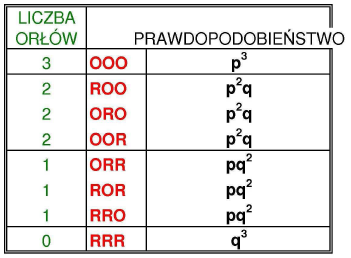
dodanie prawdopodobieństw dla tej samej liczby orłów

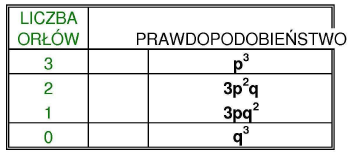
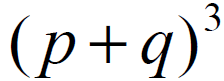
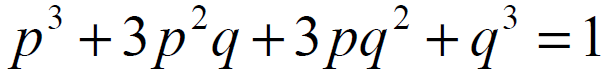
ROZKŁAD DWUMIANOWY,

będący rozwinięciem wzoru

TRÓJKĄT PASCALA:

przedstawia współczynniki równania, będącego rozwinięciem dwumianu dla właściwej liczby n:

Obliczanie prawdopodobieństwa uzyskania

k liczby zdarzeń („sukcesów”) w n próbach:

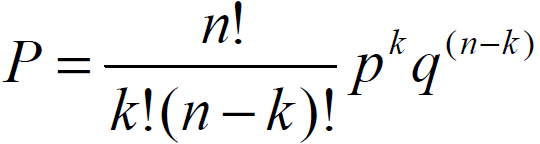
n - liczba prób

k - liczba sukcesów

p - prawdopodobieństwo sukcesu w pojedynczej próbie

q - prawdopodobieństwo porażki w pojedynczej próbie

ZADANIE 1.

Jakie jest prawdopodobieństwo, że w czterech rzutach orzeł wypadnie trzykrotnie ?

n = 4 k = 3 (orły) p = ½ q = ½ p + q = 1

4 !

P = (¹/₂) ³ (¹/₂) ^{(4 - 3)} P = ⁴/₁ * ¹/₈ * ¹/₂ = ⁴/₁₆

3 ! (4 - 3) !

ROZKŁAD PRAWDOPODOBIEŃSTW:

• w miarę wzrostu liczby prób w rozkładzie dwumianowym,

rozkład przybliża się do postaci normalnej, np. liczba prób = 10

rozkład dwumianowy: liczba prób rozkład

liczba orłów/ reszek: prawdopodobieństwo:

0 ¹/₁₀₂₄ 0,00097656

1 ¹⁰/₁₀₂₄ 0,00976563

2 ⁴⁵/₁₀₂₄ 0,04394531

3 ¹²⁰/₁₀₂₄ 0,1171875

4 ²¹⁰/₁₀₂₄ 0,20507813

5 ²⁵²/₁₀₂₄ 0,24609375

6 ²¹⁰/₁₀₂₄ 0,20507813

7 ¹²⁰/₁₀₂₄ 0,1171875

8 ⁴⁵/₁₀₂₄ 0,04394531

9 ¹⁰/₁₀₂₄ 0,00976563

10 ¹/₁₀₂₄ 0,00097656

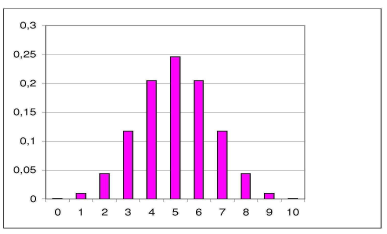
3 zdarzenia pozostałe zdarzenia

centralne

60 % przypadków 40 % przypadków

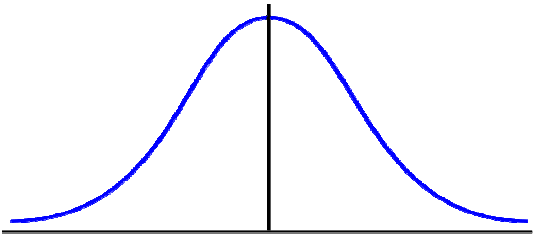
ROZKŁAD NORMALNY:

σ σ

• oś symetrii = ŚREDNIA = MEDIANA = DOMINANTA (ta sama wartość)

GĘSTOŚĆ ROZKŁADU NORMALNEGO:

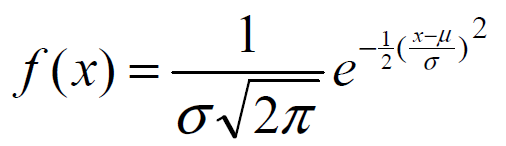
μ - średnia

σ - odchylenie standardowe

e - podstawa logarytmu naturalnego

KRZYWA ROZKŁADU NORMALNEGO (FUNKCJI GĘSTOŚCI):

• symetryczna względem prostej x = μ

• w punkcie x = μ osiąga wartość maksymalną

• 
  PUNKTY PRZEGIĘCIA ramion krzywej dla x = μ - σ x = μ + σ

• kształt funkcji gęstości (krzywej) zależy od wartości parametrów:

μ σ

przesunięcie krzywej „smukłość” krzywej

REGUŁA 3 SIGM:

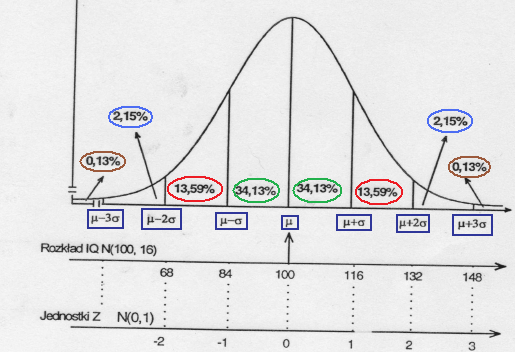
• kolejne odchylenia standardowe od średnie w obu kierunkach

• % populacji w poszczególnych przedziałach:

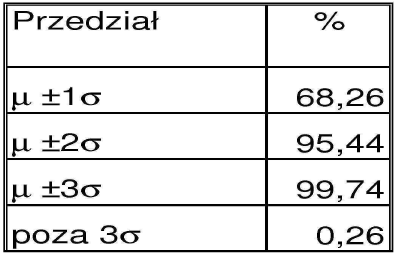
badanie:

WYNIKI SUROWE NORMALIZACJA ustalenie, że

ŚREDNIA = 100

REGUŁA 6 SIGM:

• rozszerzenie 3 sigm

• metoda zarządzania jakością (przemysł)

• określa liczbę dopuszczalnych wadliwych wyrobów poza 3 odchyleniem

(kilka na milion)

STANDARYZACJA ROZKŁADU:

• sprowadzenie dowolnego rozkładu normalnego o danych parametrach μ i σ do ROZKŁADU STANDARYZOWANEGO o wartości oczekiwanej μ = 0 i odchyleniu standardowym σ = 1

ROZKŁAD NORMALNY ROZKŁAD STANDARYZOWANY

μ i σ μ = 0 N (0,1)

σ = 1

μ σ

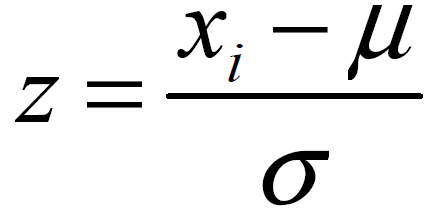
z - wartość wystandaryzowana

x_i - wartość, dla której standaryzowanie

μ - średnia

• umożliwia porównywanie wyników z różnych pomiarów

μ

z (-)

z z (+)

ZADANIE 1.

Studenci:

A B

μ = 50 μ = 80

σ = 7 σ = 10

x_i = 60 x_i = 95

Standaryzacja wyników z testów:

z = 60 - 50 / 7 = 1,43 z = 95 - 80 / 10 = 1,5

A B

0 1 2

μ (1 σ) (2 σ)

ZADANIE 2.

Jaki % populacji osiągnie wyniki wyższe niż 125 pkt? 50 %

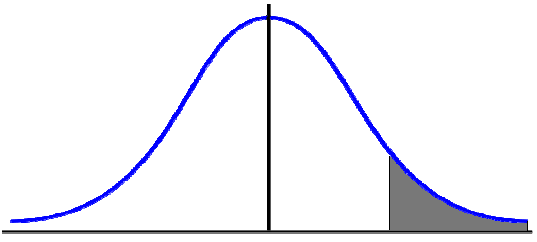
Test

μ = 100

σ = 20

μ 125

z = 125 - 100 / 20 = 1,25

pole powierzchni pod krzywą normalną

3944 39,44 %

50 % - 39,44 % = 10,56 %

TABLICA POWIERZCHNI:

Z

drugie miejsce po przecinku

pierwsze miejsce po przecinku

np. 3944 = 0,3944 = 39,44 %

10000

Pole powierzchni z tablicy = pole pomiędzy szukanym wynikiem a średnią

50 % 50 %

średnia

50 % - „tablica” = szukany wynik

ZADANIE 3.

Jaki % populacji osiągnie wyniki między 80 a 115 pkt?

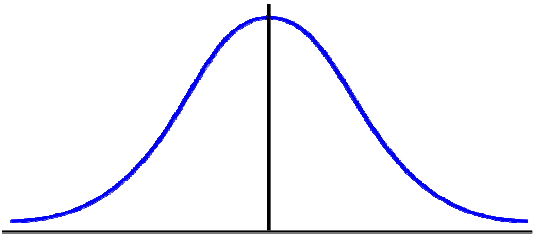
Test

μ = 100

σ = 20

80 100 115

policzyć pole jednego i drugiego i dodać

pole:

z = 80 - 100 / 20 = -1 0,3413 0,6147 61,47 %

z = 115 - 100 / 20 = 0,75 + 0,2734

ZADANIE 4.

Pomiędzy jakimi wynikami znajdzie się środkowe 25 % populacji? środkowa 25 % ćwiartka

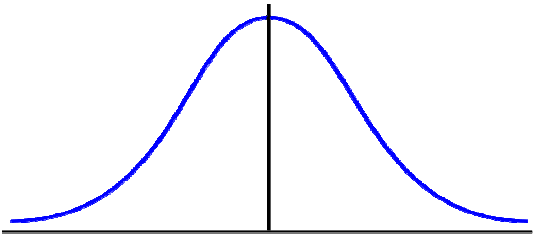
Test

μ = 100

σ = 20

? 100 ? ¹/₈ 0,125

x_i - μ

z = σ

z σ = x_i - μ

x_i = μ + |z| σ

wartość bezwzględna, bo wyniki z dwóch stron średniej

Tabela szukanie z wybiera się najmniejsze pole powierzchni, gdy na granicy

x₁ = 100 + 0,32 * 20 = 106,4

x₂ = 100 - 0,32 * 20 = 93,6

ZADANIE 5.

Jan uzyska w teście 150 pkt, 84 % uzyskało gorsze wyniki. Jaki był średni wynik?

84 %

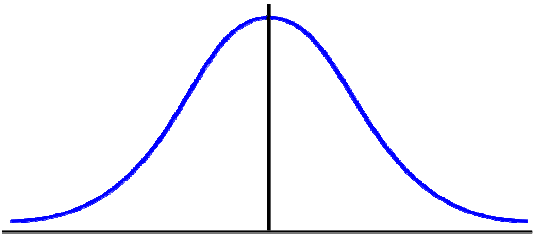
Jan 150 pkt σ = 30

μ = ?

μ 150

x_i - μ z = 1

z = σ μ = 150 - 1 * 30 = 120

z σ = x_i - μ

μ = x_i - z σ

SPSS:

OPIS STATYSTYCZNY ZMIENNEJ:

ANALIZA OPIS STATYSTYCZNY CZĘSTOŚCI ZMIENNA

STATYSTYKI

TENDENCJA CENTRALNA: dominanta

WYKRESY

KOŁOWY

RAPORT:

Tabela 1.

DOMINANTA: np. 2 sprawdzić, co oznacza 2:

ZMIENNE WARTOŚCI ETYKIETY

np. 2 - ...

Tabela 2.

wartości zmiennej przedstawione w kolejności

UWAGA: oznaczenia w etykiecie mogą zaczynać się od 0 (lub częściej od 1)

WYRZUCAĆ PROCENT SKUMULOWANY !!!

Rozproszenie: LICZBA KATEGORII

ANALIZA OPIS STATYSTYCZNY CZĘSTOŚCI ZMIENNA

STATYSTYKI

TENDENCJA CENTRALNA: mediana, dominanta

WARTOŚCI PERCENTYLI: percentyle, kwartyle

WYKERSY

SŁUPKOWY

MEDIANA: ... - co oznacza ...? WARTOŚCI

PERCENTYLE: 25 = ... pierwsze 25 % próby do ... i ...

ODCHYLENIE ĆWIARTKOWE:

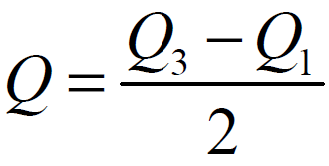
WSPÓŁCZYNNIK ZMIENNOŚCI:

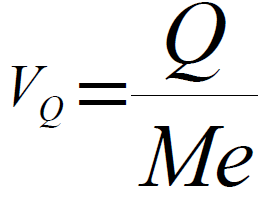
0 - mała zmienność

0,5 - umiarkowana zmienność

1 - duża zmienność

ANALIZA OPIS STATYSTYCZNY CZĘSTOŚCI ZMIENNA

STATYSTYKI

TENDENCJA CENTRALNA: mediana, dominanta, średnia

WARTOŚCI PERCENTYLI: percentyle, kwartyle

ROZPROSZENIE: odchylenie standardowe

ROZKŁAD: skośność, kurtoza

WYKERSY

HISTOGRAM

(+ krzywa)

DOMINANTA:

może mieć więcej wartości modalnych

WSPÓŁCZYNNIK ZMIENNOŚCI:

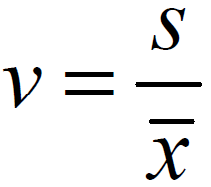
ODCHYLENIE ĆWIARTKOWE

50 %

34 %

ZMIENNE NOMINALNE

ZMIENNE PORZĄDKOWE

ZMIENNE ILOŚCIOWE

---