PROWADZĄCY: Dr Henryk Pykacz INSTYTUT FIZYKI POLITECHNIKI WROCŁAWSKIEJ LABORATORIUM Z FIZYKI
WYKONAWCY : SPR. EDYTA BUCZYŃSKA			GRUPA : 0	ROK AK. 1	SEMESTR : 2
(EWA JAGIELSKA)			WYKONANO : 25.04.1995	ODDANO : 09.05.1995	OCENA :
NR ĆWICZ. 22	TEMAT : POMIAR TEMPERATURY PIROMETREM OPTYCZNYM

1.WSTĘP TEORETYCZNY

Każde ciało znajdujące się w temperaturze wyżej niż 0 K jest źródłem promieniowania termicznego, wywołanego ruchem cieplnym cząsteczek i atomów, a zarazem odbiornikiem takiego promieniowania. Promieniowanie padające na ciało może być przez nie odbite, pochłonięte lub przepuszczone. Stosunek strumienia energii promieniowania pochłoniętego przez ciało do strumienia energii promieniowania padającego na nie nazywamy współczynnikiem pochłaniania.Współczynnik ten załeży od składu chemicznego, stanu powierzchni, temperatury oraz składu spektralnego, padającego na ciało promieniowania. Naukowcy wprowadzili dwa idealne przypadki:

1.CIAŁO SZARE którego współczynnik pochłaniania nie zależy od

długości fali (A()=const dla T=const);

2.CIAŁO DOSKONALE CZARNE - całkowicie pochłaniające promieniowenie

( A(,T)=1 ).

Inną wielkością, występującą w badanym zjawisku ,jest emitancja, czyli moc wypromieniowania na jednostkę powierzchni.Emitancję ciała rzeczywistego pozwala nam znaleźć prawo Kirchoffa, które mówi, że :stosunek spektralnej emitancji ciała rzeczywistego do jego spektralnego współczynnika pochłaniania jest równe spektralnej emitancji ciała doskonale czarnego.Musimy zatem znać emitancję ciała doskonale czarnego.

Emitancję tę określił Planck, wyprowadzając wzór :

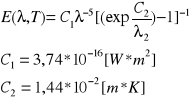
Jak możemy wywnioskować z wykresu przy wyższych temperaturach

emitowane jest więcej energii przy niższych długościach fali. Analizując wzór Plancka, kilku fizyków doszło do wielu ważnych wniosków. Mianowicie Boltzman zauważył, że po obliczeniu równania Plancka i wykonaniu kilku odpowiednich działań uzyskuje się zależność :

Tak więc uzyskujemy bezpośrednią zależność emitancji ciała doskonale

czarnego od temperatury.Inny fizyk Wien, sformułował prawo podające zależność długości fali, dla której krzywa spektralnej emitancji ciała doskonale czarnego ma max, od temperatury. Tak więc Wien stwierdził, że : iloczyn

temperatury ciała doskonale czarnego i długości fali, dla której występuje max zdolności emisyjnej, ma wartość stałą.

\/

2.CEL ĆWICZENIA I OPIS JEGO PRZEBIEGU.

Celem ćwiczenia było zapoznanie się z jedną z metod pomiaru temperatury. Pomiaru tego dokonywaliśmy za pomocą pirometru optycznego. Pirometr służy do pomiaru temp. czarnej badanego obiektu. Obiektyw pirometru tworzy obraz badanego ciała w płaszczyźnie włókna żarówki umieszczinej przed okularem. Obserwator patrzący przez okular pirometru widzi więc włókno żarówki na tle obrazu badanego ciała. W okularze mieści się filtr szklany, przepuszczający tylko niwielki przedział promieniowania. Emitancję włókna można zmieniać regulując rezystancję w obwodzie zasilania. Jeżeli włókno żarówki pirometru było takiej samej barwy co ciało badane, to temp.

odczytaną na pirometrze była temp. czarną ciała rzeczywistego. Opisując wzór można obliczyć temp. rzeczywistą badanego ciała.

Badaną żarówkę zasilamy w układzie

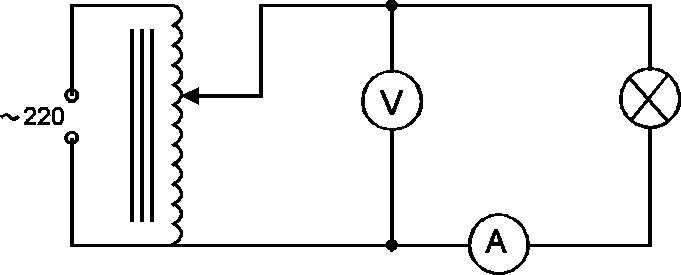
Ćwiczenie miało również na celu zbadanie zależności temp.włókna od pobranej mocy.

3.POMIARY WIELKOŚCI POŚREDNICH I OBLICZANIE WARTOŚCI SZUKANYCH.

Dane otrzymane w wyniku pomiaru oraz zamiana temperatury czarnej na rzeczywistą przy użyciu nomogramu i danego wzoru:

POMIARY DLA U=3[V]-10[V]

Lp.	U[V]	I[A]	P[ W]	Ep[%]	P[W]	Tcz[C]	Trz[K]	Trz[C]	wzórTrz[K]
1	3	1,9	0,4	7,0	5,7	1280	1633	1360	1644
2	4	2,2	0,5	5,7	8,8	1370	1743	1470	1746
3	5	2,4	0,55	4,6	12	1380	1753	1480	1758
4	6	2,7	0,64	3,9	16,2	1450	1833	1560	1838
5	7	2,9	0,70	3,4	20,3	1530	1933	1660	1930
6	8	3,2	0,78	3,0	25,6	1620	2023	1750	2034
7	8,5	3,3	0,82	2,9	28,05	1670	2083	1810	2092
8	9	3,4	0,85	2,7	30,6	1710	2123	1850	2139
9	9,5	3,5	0,87	2,6	33,25	1780	2213	1940	2221
10	10	3,6	0,92	2,55	36	1860	2253	1980	2429

POMIARY DLA U=4[V],I=2,2[A]

Lp.	U[V]	I[A]	P[W]	Ep[%]	P[W]	Tcz[C]	Trz[K]	Trz[C]	wTrz[K]	T
1	4	2,2	0,5	5,7	8,8	1370	1743	1470	1746	2
2	4	2,2	0,5	5,7	8,8	1380	1753	1480	1758	-8
3	4	2,2	0,5	5,7	8,8	1390	1753	1480	1769	-8
4	4	2,2	0,5	5,7	8,8	1410	1793	1520	1712	-48
5	4	2,2	0,5	5,7	8,8	1370	1743	1470	1746	2
6	4	2,2	0,5	5,7	8,8	1340	1713	1440	1712	32
7	4	2,2	0,5	5,7	8,8	1360	1733	1460	1735	12
8	4	2,2	0,5	5,7	8,8	1370	1743	1470	1746	2
9	4	2,2	0,5	5,7	8,8	1370	1743	1470	1746	2
10	4	2,2	0,5	5,7	8,8	1360	1733	1460	1735	12

Wyznaczanie średniego błędu kwadratowego i obliczanie błędu względnego temperatury dla pomiaru U=4[v],I=2,2[A]:

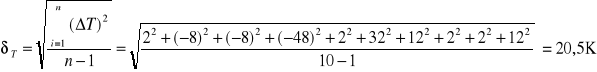
Ts=1745[K]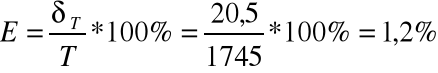

POMIARY DLA U=8[V],I=3,2[A]

Lp.	U[V]	I[A]	Tcz[C]	Ep[%]	P[W]	P[W]	Trz[K]	Trz[C]	wTrz[K]	T
1	8	3,2	1620	3,2	0,8	25,6	2023	1750	2034	15
2	8	3,2	1570	3,2	0,8	25,6	1973	1700	1976	65
3	8	3,2	1610	3,2	0,8	25,6	2013	1740	2020	25
4	8	3,2	1630	3,2	0.8	25,6	2033	1760	2045	5
5	8	3,2	1660	3,2	0,8	25,6	2063	1790	2080	-25
6	8	3,2	1680	3,2	0,8	25,6	2093	1820	2104	-55
7	8	3,2	1660	3,2	0,8	25,6	2063	1790	2080	-25
8	8	3,2	1640	3,2	0,8	25,6	2043	1770	2057	-5
9	8	3,2	1640	3,2	0,8	25,6	2043	1770	2057	-5
10	8	3,2	1630	3,2	0,8	25,6	2033	1760	2045	5

Wyznaczanie średniego błędu kwadratowego i obliczanie błędu względnego temperatury dla U=8[V],I=3.2[A]: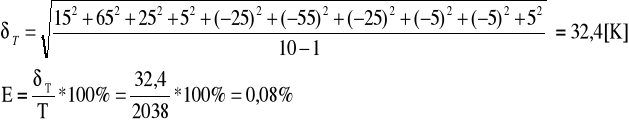

Ts=2038[K]

Metoda obliczania temperatury rzeczywistej na podstawie wzoru:

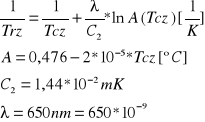
Błędy przyrządów : - woltomierz U =(1,5*10[V])/100=0,15[V]

- amperomierz I = (0,5*7,5[A])/100=0,038[A]

- pirometr T = 10 [C]

Moc P=U*I [W]

Błąd względny pomiaru mocy obliczamy z wzoru:

Błąd bezwzględny obliczamy za pomocą różniczki zupełnej

dP = IdU+UdI (przyjmujemy najmniej korzystny układ

P =IU+UI sumowania)

Błąd średni kwadratowy :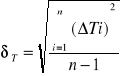

gdzie: T-średni błąd kwadratowy

Obliczanie błędu względnego temperatury:

gdzie:E-sredni błąd pojedynczego pomiaru

T-średni błąd pojedynczego pomiaru

T-średnia temperatura pojedynczego pomiaru

Ti-błąd bezwzględny pozsczególnych pomiarów

sr.T,Ti-średnia oraz składowa temperatury dla danego pomiaru

Przykładowe obliczenia:

Tcz=1620[C] U=8[V] I=3,2[A] I=0,038[A] U=0,15[V] P=IU+UI=0,8[W] E=P/P*100%=3,2% Trz=1750[C]=2023[K]

4.OCENA BŁĘDÓW I WNIOSKI.

Błędy, które są dosyć znaczne, wynikają z małej klasy dokładności mierników. Oprócz tego doświadczenie nie było wykonywane w warunkach idealnych tzn. odbicia światła dziennego w obiektywie mogły spowodować błędne odczyty. Jednak jak możemy odczytać z wykresu zależność temp. od pobranej mocy jest bardziej stroma w początkowej fazie doświadczenia, z czego możemy wywnioskować, że temp. wzrasta szybko przy mniejszym poborze mocy. Natomiast w późniejszej fazie wzrost temp o nieznaczną wartość powoduje znaczny wzrost pobranej mocy. Tak więc żarówkę powinno się wykorzystywać na poziomie "przegięcia" wykresu, w poziomie optymalnego świecenia żarówki.

---