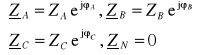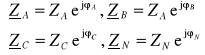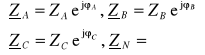Politechnika Częstochowska

Wydział Elektryczny

Katedra Elektrotechniki

Zakład Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Badanie obwodów trójfazowych

Częstochowa 2004

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z własnościami obwodów trójfazowych symetrycznych
i niesymetrycznych, ich wykresami topograficznymi oraz zjawiskami zachodzącymi w tych obwodach w przypadku istnienia różnych asymetrii.

2. Wiadomości podstawowe

2.1. Układy trójfazowe

Układem trójfazowym nazywamy zespół trzech odpowiednio połączonych obwodów elektrycznych, w których działają trzy napięcia źródłowe o jednakowej amplitudzie E_m i pulsacji , przesunięte względem siebie w fazie o kąt 120° (rys. 1):

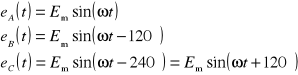
W postaci wykładniczej napięcia te można zapisać jako

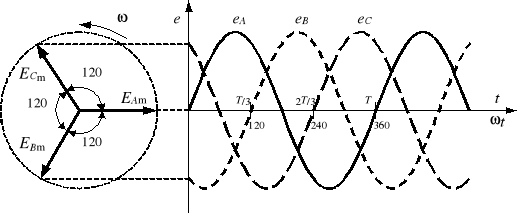
Rys. 1. Wykres wskazowy i czasowy napięć źródłowych w układzie trójfazowym o zgodnej kolejności

Z wykresu czasowego wynika, że wartości maksymalne napięć źródłowych występują po sobie w kolejności A, B, C, a na wykresie wskazowym występują one w kierunku zgodny z kierunkiem ruchu wskazówek zegara. Taki układ napięć nazywamy układem o zgodnej kolejności faz. Rozpatruje się także układy o niezgodnej kolejności faz, w których kolejność faz jest A, C, B.

Napięcia trójfazowe wytwarzane są w jednym urządzeniu zwanym generatorem trójfazowym. Każde uzwojenie generatora trójfazowego można uważać za odrębne źródło napięcia i korzystać z niego do zasilania odbiornika jednofazowego. Wtedy każde uzwojenie wraz z przyłączonym do niego odbiornikiem tworzy oddzielny obwód elektryczny. Jeżeli poszczególne obwody nie są połączone, układ trójfazowy nazywamy nieskojarzonym. Takie układy nie są stosowane w praktyce, ponieważ do przesyłu energii wymagają sześciu przewodów, a więc są nieekonomiczne.

Jeżeli poszczególne obwody są połączone ze sobą elektrycznie w określony sposób, układ trójfazowy nazywamy skojarzonym. Powoduje to zmniejszenie liczby przewodów z 6 do 3 lub 4. Trzy elementy można symetrycznie połączyć tylko na dwa sposoby: albo w gwiazdę (
) albo w trójkąt (
). Połączenia te można zastosować zarówno do uzwojeń generatora jak i do impedancji odbiornika. Ze względu na sposób kojarzenia wśród obwodów trójfazowych wyróżniamy:

• układ typu gwiazda-gwiazda (
  -
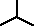
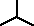
  ) bez przewodu neutralnego (trójprzewodowy),

• układ typu gwiazda-gwiazda (
  -
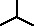
  ) z przewodem neutralnym (czteroprzewodowy),

• układ typu trójkąt-trójkąt (
  -
  ),

• układ typu gwiazda-trójkąt (
  -
  ),

• układ typu trójkąt-gwiazda (
  -
  ).

Fazą obwodu trójfazowego skojarzonego nazywamy część obwodu złożoną z uzwojenia generatora, przewodu przesyłowego oraz odbiornika energii.

Napięcia liniowe lub międzyfazowe to napięcia występujące między poszczególnymi przewodami fazowymi linii przesyłowej. Napięcia fazowe odbiornika to napięcia występujące na impedancjach poszczególnych faz odbiornika. Napięcia fazowe generatora, to napięcia występujące na uzwojeniach poszczególnych faz generatora. Dla odbiornika lub generatora połączonego w gwiazdę (
) napięcia fazowe są równe napięciom liniowym.

Prądy liniowe to prądy płynące w poszczególnych przewodach linii przesyłowej. Prądy fazowe odbiornika (generatora), to prądy płynące przez impedancje (uzwojenia) poszczególnych faz odbiornika (generatora). Dla odbiornika lub generatora połączonego w gwiazdę (
) prądy fazowe są równe prądom liniowym.

Punkt neutralny (zwany zerowym) to wspólny punkt trzech faz generatora lub odbiornika połączonych w gwiazdę. Przewód neutralny, to przewód łączący punkty neutralne generatora
i odbiornika - może on występować tylko w skojarzeniu
-
.

Generator trójfazowy nazywamy symetrycznym, gdy napięcia fazowe generatora są symetryczne (rys. 1). Odbiornik nazywamy symetrycznym, gdy impedancje poszczególnych faz odbiornika są jednakowe. Trójfazową linię przesyłową nazywamy symetryczną, gdy impedancje poszczególnych faz linii są jednakowe. Układ trójfazowy nazywamy symetrycznym, jeżeli generator, linia przesyłowa i odbiornik są symetryczne. Gdy choć jeden z powyższych warunków nie jest spełniony, układ jest niesymetryczny.

Układy trójfazowe posiadają następujące zalety:

• dla dostarczenia do odbiornika zadanej mocy wymagają najmniejszego zużycia materiału na przewody zasilające,

• powodują najmniejsze straty energii w przewodach przy danym napięciu i danej mocy przesyłowej,

• wytwarzają magnetyczne pole wirujące, które zostało wykorzystane do tanich i prostych silników indukcyjnych,

• moc chwilowa przekazywana do odbiornika jest stała w czasie.

W praktyce uzwojenia generatora łączy się w gwiazdę, natomiast odbiornik może być połączony bądź w gwiazdę, bądź w trójkąt. Z tego powodu opis analizy układów ograniczymy do opisu analizy obwodu z symetrycznym generatorze gwiazdowym, idealną linią przesyłową (impedancje linii równe 0) i odbiornikiem:

• gwiazdowym z przewodem neutralnym lub bez niego,

• trójkątowym.

2.2. Analiza prostego układu trójfazowego typu
-

W układzie pokazanym na rysunku 2 wyróżnia się:

EA, EB, EC	- napięcia fazowe generatora,
UAB, UBC, UCA	- napięcia liniowe,
VA, VB, VC	- napięcia fazowe odbiornika,
VN	- napięcie między punktami neutralnymi odbiornika i generatora,
JA, JB, JC	- prądy liniowe, będące jednocześnie prądami fazowymi,
JN	- prąd w przewodzie neutralnym,
ZA, ZB, ZC	- impedancje fazowe odbiornika,
ZN	- impedancja przewodu neutralnego,
0, N	- punkty neutralne odpowiednio generatora i odbiornika.

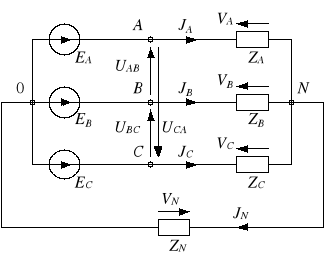
Rys. 2. Układ trójfazowy typu gwiazda-gwiazda

Dane:

Co najwyżej jedna z podanych impedancji może być równa zeru. Ponieważ generator jest symetryczny, to moduł napięcia liniowego wynosi U =
.

Obliczenia przeprowadza się następująco:

1. Obliczamy potencjał punktu N względem punktu 0 (metoda dwóch węzłów):

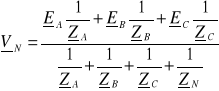
Przypadki szczególne:

• gdy impedancja Z_N = 0, potencjał V_N = 0,

• gdy Z_A = 0 lub Z_B = 0 lub Z_C = 0, potencjał V_N wynosi odpowiednio E_A, E_B lub E_C.

2. Obliczamy spadki napięć na impedancjach odbiornika:

3. Obliczamy prądy:

Gdy któraś z impedancji jest równa zeru, należy skorzystać z I prawa Kirchhoffa:

• dla układu trójprzewodowego (Z_N = ∞):
  ,

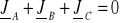
• dla układu czteroprzewodowego (Z_N ≠ ∞):
  .

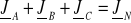
4. Napięcia liniowe oblicza się wg wzorów:

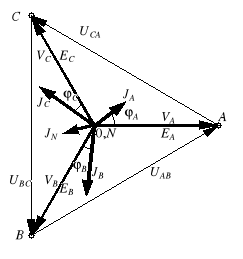
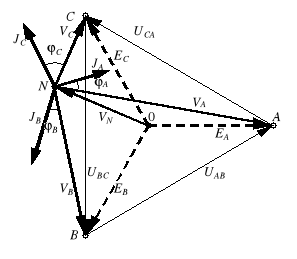
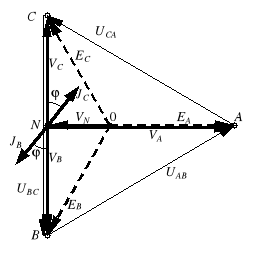
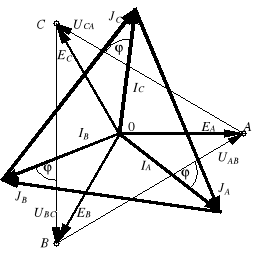
Obliczenia analityczne wygodnie jest zobrazować na wykresie topograficznym (rys. 3). Zaczynamy od narysowania gwiazdy napięć generatora i zaznaczenia napięcia V_N. Następnie zaznaczamy napięcia fazowe (np. wskaz V_A rysujemy od punktu N do punktu A) i liniowe
(np. wskaz U_AB rysujemy od B do A). Wreszcie umieszczamy wskazy prądów - najpierw nanosimy wskazy prądów wyznaczonych z prawa Ohma, a prąd obliczony na podstawie I prawa Kirchhoffa, zaznaczamy jako ostatni, sumując wszystkie wskazy prądów i biorąc sumę ze znakiem minus.

a)	b)
układ symetryczny
c)	d)
e)	f)
przerwa w fazie A	zwarcie fazy A

Rys. 3. Wykresy topograficzne prądów i napięć układu gwiazda-gwiazda dla wybranych przypadków

2.3. Analiza układu trójfazowego typu
-

W układzie pokazanym na rysunku 4 wyróżnia się:

EA, EB, EC	- napięcia fazowe generatora,
UAB, UBC, UCA	- napięcia liniowe, będące zarazem napięciami fazowymi odbiornika,
IA, IB, IC	- prądy fazowe odbiornika,
JA, JB, JC	- prądy liniowe,
ZA, ZB, ZC	- impedancje fazowe odbiornika,

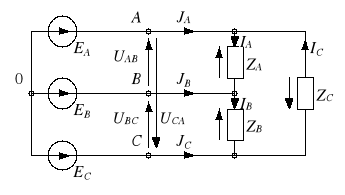
Rys. 4. Układ trójfazowy typu gwiazda-trójkąt

Dane:

Żadna z podanych impedancji może być równa zeru. Ponieważ generator jest symetryczny, to moduł napięcia liniowego wynosi U =
.

Obliczenia przeprowadza się następująco:

1. Oblicza się napięcia liniowe:

2. Oblicza się prądy fazowe odbiornika:

3. Oblicza się prądy liniowe:

Jeśli układ jest symetryczny, to moduł prądu liniowego J =
, a ponadto

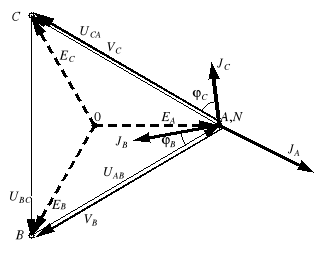
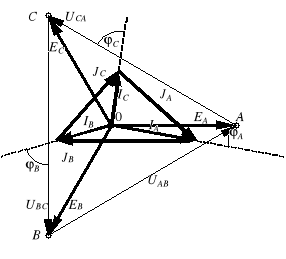
Obliczenia analityczne wygodnie jest zobrazować na wykresie topograficznym (rys. 5). Najpierw rysujemy układ napięć fazowych generatora i układ napięć liniowych. Następnie zaznaczamy prądy fazowe odbiornika. Wskazy prądów liniowych łatwo otrzymać łącząc końce wskazów odpowiednich prądów fazowych (np. wskaz J_A zaczyna się w końcu wskazu I_C i kończy
w końcu wskazu I_A).

W symetrycznym układzie trójfazowym obliczenia wystarczy przeprowadzić dla fazy A, gdyż prądy i napięcia w fazach B i C są przesunięte odpowiednio o -120° i +120° względem prądów
i napięć fazy A. Pozwala to znacznie skrócić czas obliczeń.

a)	b)
układ symetryczny

Rys. 5. Wykresy topograficzne napięć i prądów wybranych układów gwiazda-trójkąt

2.4. Moc w układach trójfazowych

W dowolnym układzie trójfazowym całkowita moc odbiornika jest równa sumie mocy poszczególnych jego faz:

lub w postaci symbolicznej

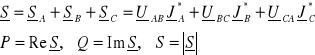
W układzie trójfazowym symetrycznym moce poszczególny faz są równe, co prowadzi do zależności:

gdzie U - moduł napięcia liniowego, J - moduł prądu liniowego,  - kąt fazowy impedancji odbiornika. Powyższe zależności są prawdziwe niezależnie od tego, czy odbiornik jest gwiazdowy, czy trójkątowy.

2.5. Wyznaczanie kolejności faz

Jeśli zaciski fazowe układu napięć trójfazowych nie są oznaczone i nie wiadomo, który zacisk jest fazą A, który B, a który C, do ich określenia można posłużyć się prostym układem. Oznaczając zaciski tymczasowo przez 1, 2, 3 podłączamy do nich układ z rysunku 7 (punkt 3.1), przy czym reaktancja cewki X powinna być równa w przybliżeniu rezystancji żarówek R.

Jeśli zaciski 1, 2, 3 tworzą układ kolejności zgodnej, to otrzymujemy

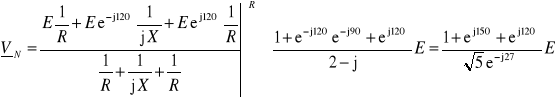
Wyrażenie to można uprościć, przekształcając odpowiednio licznik:

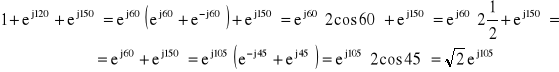
gdzie skorzystano ze wzoru

Wobec tego

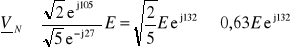
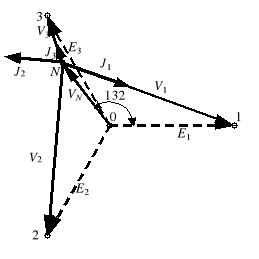
W dalszym ciągu wygodnie jest naszkicować wykres topograficzny (rys. 6a). Wynika z niego, że napięcie fazowe V₁ jest większe niż napięcie fazowe V₃. Ponieważ żarówki 1 i 3 są jednakowe, żarówka 1 będzie świecić jaśniej niż żarówka 3.

Jeśli natomiast zaciski 1, 2, 3 tworzą układ kolejności przeciwnej, to

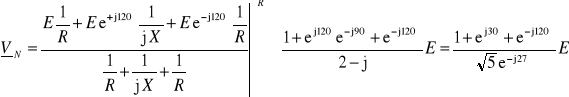
Postępując jak poprzednio, otrzymujemy

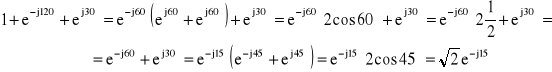
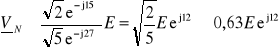
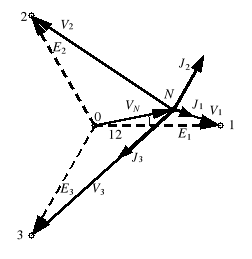
Posiłkując się ponownie wykresem topograficznym (rys. 6b), stwierdzamy, że tym razem żarówka 1 powinna świecić słabiej niż żarówka 3.

Tak więc gdy żarówka 1 świeci mocniej niż żarówka 3, zaciski 1, 2, 3 tworzą układ trójfazowy kolejności zgodnej i można je oznaczyć A, B, C. Natomiast gdy żarówka 1 świeci słabiej niż żarówka 3, układ 1, 2, 3 jest kolejności przeciwnej i zaciski można oznaczyć jako A, C, B.

a)	b)

Rys. 6. Wykresy topograficzne do wyznaczania kolejności faz: a) kolejność zgodna, b) kolejność przeciwna

3. Przebieg ćwiczenia

3.1. Wyznaczanie kolejności faz

Pomiary w tym punkcie przeprowadzać opcjonalnie (wg uznania prowadzącego ćwiczenia).

• Zestawić układ wg schematu z rysunku 7, zaciski 1, 2 i 3 wybrać losowo z zacisków fazowych strony wtórnej autotransformatora,

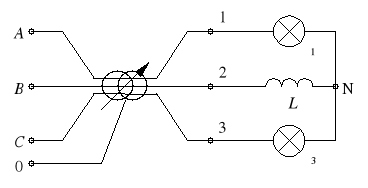
Rys. 7

• Stwierdzić, która żarówka świeci jaśniej (1 czy 3) i na tej podstawie (wiedząc, że od strony pierwotnej autotransformatora kolejność faz jest zgodna) wyznaczyć kolejność faz na zaciskach wyjściowych transformatora A, B, C (punkt 2.5); sprawdzić, czy wyznaczona kolejność faz pokrywa się z oznaczeniami na autotransformatorze.

3.2. Pomiary w układzie gwiazdowym

• Zestawić układ wg schematu z rysunku 8,

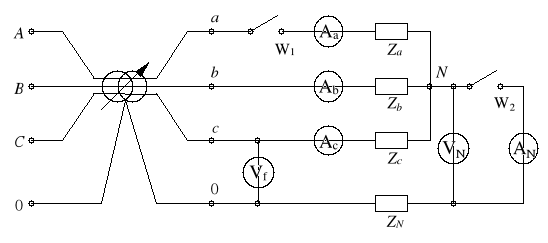
Rys. 8

• Dla różnych położeń wyłączników W₁ i W₂ oraz przy różnych obciążeniach dokonać pomiarów napięć i prądów (tabela 1) (UWAGA: wszelkie manipulacje łączeniowe należy wykonywać przy wyłączonym napięciu zasilania),

• Napięcie zasilania podaje prowadzący (zwykle napięcie fazowe wynosi około 40 V),

• W przypadku zwarcia fazy (Z_a = 0) koniecznie otworzyć wyłącznik W₂.

3.3. Pomiary w układzie trójkątowym

• Zestawić układ wg schematu z rysunku 9,

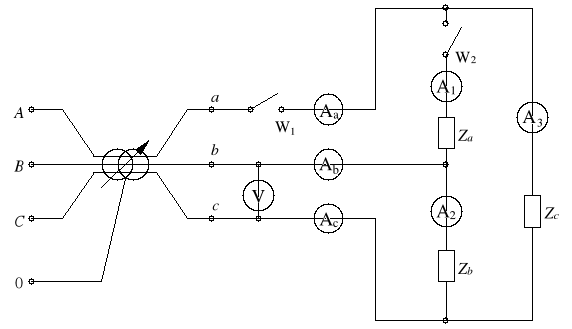
Rys. 9

• Pomiary przeprowadzać podobnie jak w poprzednim punkcie (tabela 2).

Tabela 1 (dla odbiornika gwiazdowego)

Lp.

Układ połączeń

Prze­wód zero­wy

W1

W2

Impedancje

Pomiary

Obliczenia

Za

Zb

Zc

ZN

Uf

UN

IA

IB

IC

IN

UN

IA

IB

IC

IN

SA

SB

SC

S









V

V

A

A

A

A

V

A

A

A

A

VA

VA

VA

VA

1

symetryczny

jest

Z

Z

R

R

R

RN

2

brak

Z

O

R

R

R

∞

3

przerwa w fazie A

jest

O

Z

∞

R

R

RN

4

brak

O

O

∞

R

R

∞

5

zwarcie fazy A

brak

Z

O

0

R

R

∞

6

niesymetryczny (Za ≠ Zb ≠ Zc, ZN = 0)

jest

Z

Z

R

L

C

0

7

brak

Z

O

R

L

C

∞

8

(Za = Zb ≠ Zc, ZN ≠ 0)

jest

Z

Z

R

R

C

RN

Z - zamknięty, O - otwarty

Dane: R = 55  (dla U_f = 85 V), L = 0,11 H, C = 40 F, Z_N = j79,6 

Tabela 2 (dla odbiornika trójkątowego)

Lp.

Układ połączeń

W1

W2

Impedancje

Pomiary

Obliczenia

Za

Zb

Zc

U

I1

I2

I3

IA

IB

IC

I1

I2

I3

IA

IB

IC

SA

SB

SC

S







V

A

A

A

A

A

A

A

A

A

A

A

A

VA

VA

VA

VA

1

symetryczny

Z

Z

R

R

R

2

przerwa w linii A

O

Z

R

R

R

3

przerwa w fazie A

Z

O

∞

R

R

4

niesymetryczny

Z

Z

R

L

C

Z - zamknięty, O - otwarty

Dane: R = 66  (dla U = 105 V), L = 0,11 H, C = 40 F

4. Opracowanie sprawozdania

1. Cel ćwiczenia.

2. Schematy pomiarowe i tabele wyników.

3. Parametry i dane znamionowe zastosowanych przyrządów.

4. Wyznaczenie kolejności faz - opis sposobu i wyniki.

5. Zamieścić obliczenia poparte wykresami wskazowymi dla każdego przypadku pomiarowego.

6. Uzupełnić tabele.

7. Wnioski.

5. Pytania sprawdzające

1. Co to jest obwód trójfazowy?

2. Kiedy obwód trójfazowy jest symetryczny?

3. Jakie są zalety układów trójfazowych.

4. Omówić tok obliczeń układu trójfazowego dla odbiornika gwiazdowego symetrycznego.

5. Omówić tok obliczeń trójfazowego dla odbiornika gwiazdowego niesymetrycznego trój-
   i czteroprzewodowego.

6. Omówić tok obliczeń układu trójfazowego dla odbiornika trójkątowego symetrycznego.

7. Omówić tok obliczeń układu trójfazowego dla odbiornika trójkątowego niesymetrycznego.

8. Omówić schemat do wyznaczania kolejności faz i zasadę pomiaru.

9. Zamienić w schemacie do wyznaczania kolejności faz cewkę na kondensator i przeprowadzić rozumowanie jak w punkcie 2.5. Która z żarówek będzie świecić jaśniej w przypadku zgodnej kolejności faz?

10. Narysować wykresy wskazowe dla rozpatrywanych w ćwiczeniu przypadków.

Literatura

[1] Bolkowski S.: Elektrotechnika teoretyczna, tom I - teoria obwodów elektrycznych, WNT,
W-wa 1986, ss. 200-219.

[2] Bolkowski S., Matusiak R.: Podstawy elektrotechniki, część 2, Wydawnictwa Politechniki Warszawskiej, W-wa 1971.

[3] Cholewicki T.: Elektrotechnika teoretyczna, tom I, WNT, W-wa 1970, ss. 547-612.

[4] Krakowski M.: Elektrotechnika teoretyczna, tom I - obwody liniowe i nieliniowe, PWN, W-wa 1991, ss. 187-207.

[5] Kurdziel R.: Podstawy elektrotechniki, WNT, W-wa 1973.

[6] Lubelski K.: Elektrotechnika teoretyczna, część 4, skrypt Politechniki Częstochowskiej, Cz-wa 1979.

Badanie obwodów trójfazowych

11

Politechnika Częstochowska, Wydział Elektryczny, Katedra Elektrotechniki

---