Filtracja

Filtracja jest procesem, w którym z mieszaniny cieczy z cząstkami stałymi usuwa się część jednej z faz. W efekcie procesu filtracji powstaje klarowna ciecz i zatężona zawiesina o różnej zawartości cieczy. Można wyróżnić dwa zakresy procesu filtracji. Jeśli filtruje się zawiesinę zawierającą niewielkie ilości cząstek stałych, to proces taki nazywa się filtracją oczyszczającą, a jeśli filtruje się zawiesinę o większych zawartościach ciała stałego, to proces nazywa się filtracją rozdzielającą. W obu rodzajach procesów rozmiary cząstek ciała stałego mogą przyjmować bardzo różnorodne rozmiary od kilku μm do kilku cm.

W procesach filtracji zawsze występuje jakaś przegroda filtracyjna. Funkcję przegrody mogą spełniać:

• usypane warstwy filtrujące,

• masy porowate, spieki, bibuły,

• tkaniny filtracyjne,

• własny osad wydzielony z zawiesiny (placek filtracyjny), osad może być nieściśliwy bądź ściśliwy.

Przegroda filtracyjna zawsze stawia opór przy przepływie cieczy, opór ten (spadek ciśnienia) można obliczyć ze zmodyfikowanego równania Darcy-Weisbacha w postaci:

Współczynnik oporu przepływu
w takim przypadku należy obliczać jak dla ruchu laminarnego (bo wszystkie procesu odbywają się powoli), a zależność w tym obszarze, tj. dla
ma postać:

gdzie:

stała zależna od kształtu ziaren,

Aby pokonać opory przepływu cieczy przez warstwę przegrody filtracyjnej należy zastosować różnicę ciśnień po jej obu stronach. Jeśli nad przegrodą panuje ciśnienie atmosferyczne, to pod nią należy wytworzyć podciśnienie, natomiast jeśli pod przegrodą panuje ciśnienie atmosferyczne, to nad nią należy wytworzyć podciśnienie.

W celu obliczenia wydajności filtra (strumienia objętości cieczy)
należy dokonać przekształceń wykorzystując powyższe równania i równanie ciągłości, co prowadzi do zależności:

Kłopotliwe do doświadczalnej weryfikacji liczby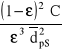
łączy się i zastępuje pojęciem oporu warstwy filtracyjnej R_o, co prowadzi do zależności zwanej równaniem Carmanna:

Opór warstwy filtracyjnej R_o wyznacza się doświadczalnie.

Filtracja plackowa

W czasie filtracji przez własny osad (filtracji plackowej) grubość warstwy filtracyjnej L systematycznie narasta, zatem można obserwować stały spadek szybkości odbioru filtratu (
) lub jeśli chce się zachować stałą szybkość odbioru, to należy systematycznie zwiększać różnicę ciśnień po obu stronach przegrody filtracyjnej. W celu dokonania matematycznego opisu takiego procesu należy rozpatrzyć go różniczkowo.

Wprowadźmy najpierw pojęcie stosunku masowego ciała stałego zawartego w zawiesinie:

i wybierzmy różniczkowy czas
, w którym z zawiesiny ubywa
ciała stałego i ta sama masa
pojawia się w placku powodując wzrost jego grubości o dL. Załóżmy dodatkowo, że placek jest nieściśliwy, porowatość placka jest stała, a ciało stałe osadza się tylko na powierzchni placka.

Bilansując obie fazy uzyskuje się:

Różniczkowy ubytek masy filtratu:

Różniczkowy przyrost masy placka filtracyjnego:

Z kolei różniczkowy przyrost objętości placka filtracyjnego wynosi:

,

a więc różniczkowy przyrost grubości placka wynosi:

Wartość porowatości placka
można wyznaczyć eksperymentalnie za pomocą prostych pomiarów.

Masa ciała stałego w placku filtracyjnym wynosi:

Ta sama masa może być wyznaczona z ubytku ciała stałego w zawiesinie:

Przekształcając oba równania otrzymuje się zależność:

z której wynika, że wystarczy wykonanie jednego eksperymentu, w którym zmierzone zostaną: objętość filtratu
, różnica stężeń ciała stałego w zawiesinie przed i po procesie
, oraz grubość placka L.

Aby opisać przebieg procesu w czasie filtracji należy różniczkowe równanie określające grubość placka filtracyjnego scałkować od początku do końca procesu. Jak pisano wcześniej możliwe są dwa różne przebiegi procesu filtracji plackowej.

• Filtracja przy stałej szybkości odbioru filtratu

W procesie filtracji o stałej szybkości odbioru filtratu musi ulegać zmianie różnica ciśnień po obu stronach przegrody filtracyjnej, a stała pozostaje wartość
. Zatem:

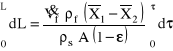
Jeśli do powyższego równania po lewej stronie wstawić zależność wynikającą z równania Carmanna, to można określić jaką różnicę ciśnień należy zastosować w każdym momencie procesu:

Jak widać różnica ciśnień jaką należy zastosować w procesie filtracji o stałej szybkości odbioru filtratu jest wprost proporcjonalna do czasu i do kwadratu szybkości odbierania filtratu, a odwrotnie proporcjonalna do kwadratu pola powierzchni fitlracji.

• Filtracja przy stałej różnicy ciśnień

Proces filtracji przy stałej różnicy ciśnień (w skrócie nazywany filtracją przy stałym ciśnieniu) jest najczęściej spotykaną formą filtracji plackowej. W celu uzyskania równania opisującego przebieg tego procesu w czasie należy do podstawowego równania różniczkowego wstawić zależność Carmanna i dokonać całkowania od początku do końca procesu:

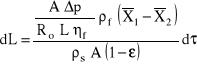
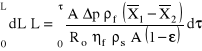
po scałkowaniu

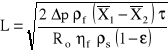
Wstawiając jeszcze raz grubość osadu wyznaczoną z równania Carmanna

i dokonując przekształceń uzyskuje się zależność:

,

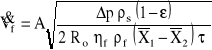
z której wynika, że szybkość odbioru filtratu maleje z czasem w potędze ½ i jest proporcjonalna do różnicy ciśnień po obu stronach przegrody.

Interesujące jest, jaka jest objętość filtratu uzyskiwanego po pewnym czasie
. Wielkość tę można otrzymać całkując szybkość filtracji w całym procesie zgodnie z zależnością:

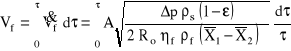
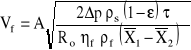
Kolejną wielkością interesującą ze względów procesowych jest grubość placka filtracyjnego, którą można obliczyć przytoczone wcześniej równania bilansowe:

Skąd:

Podczas filtracji różnych zawiesin, a w szczególności materiału biologicznego może wystąpić osad mający specyficzną właściwość, przejawiającą się porowatością zmienną w trakcie procesu. Osad taki nazywamy osadem ściśliwym. W tym szczególnym przypadku opór osadu
zależy od różnicy ciśnień
zgodnie z zależnością:

Wykładnik s nazywany jest współczynnikiem ściśliwości i przybiera wartości w obszarze
. Jeśli współczynnik ściśliwości jest równy 0, to osad jest nieściśliwy i wówczas obowiązują wszystkie prawa wyprowadzone wyżej. Jeśli mamy osad ściśliwy, to poczynając od równania Carmanna należy uwzględnić zależność oporu osadu od ciśnienia i otrzymuje się wówczas wzór:

4

---