Temat: Wektor położenia. (wektorowy opis ruchu)

Cele poznawcze i kształcące

Uczeń wie:

• Co nazywamy układem odniesienia;

• Co określa wektor wodzący;

• Co nazywamy przemieszczeniem ciała;

Poznanie tematu przez:

• Krótki wykład;

• Powtórzenie z uczniami;

• Wykonanie kilku zadań;

Materiały i środki dydaktyczne:

• Książka;

• Tablica;

• Ćwiczenia;

Przebieg lekcji:

1. Część nawiązująca:

• Czynności organizacyjne, sprawdzenie obecności;

• Przypomnienie wiadomości potrzebnych do przeprowadzenia lekcji przez wybranego ucznia wspólnie z klasą;

• Wyjaśnienie uczniom na czym będzie polegała ich praca na lekcji;

• Część postępująca:

• Zapisanie tematu lekcji na tablicy;

• Omówienie tematu;

• Przeprowadzenie ćwiczeń i wykonanie kilku zadań dla utrwalenia materiału i sprawdzenia, czy poznane na lekcji wiadomości są zrozumiałe;

3. Podsumowanie:

• Prowadzący wraz z uczniami podsumowuje temat, powtórzenie wiadomości poznanych na dzisiejszej lekcji;

• Zadanie zadania domowego;

Cel główny lekcji: Poznanie wektorowej metody opisu ruchu.

Uwagi:

Szczegółowe opracowanie przebiegu lekcji:

a) Czynności wstępne

• Sprawdzenie obecności;

• Określenie celu lekcji i napisanie tematu lekcji na tablicy;

2. Przypomnienie potrzebnych wiadomości i umiejętności:

Dodawanie wektorów leżących na jednej prostej

o zgodnych kierunkach i zwrotach: o jednakowych kierunkach i przeciwnych zwrotach:





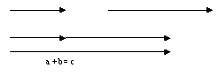
Dodawanie wektorów

Przypuśćmy, że ktoś wyszedł z punktu A, przeszedł 4 m na wschód, następnie 3 m na północ i doszedł do punktu B. Ostatecznie jest w miejscu odległym o 5 m od punktu wyjścia - wynika to z Twierdzenia Pitagorasa. Jest to przykład dodawania wektorów. Dwa wektory przesunięcia o długości 3 m i 4 m, dodajemy po to, by dostać przesunięcie wypadkowe - wektor przesunięcia o długości 5 m.

Ta zasada obowiązuje dla każdego rodzaju wektorów.

Mamy dwie siły 3 N i 4 N, działające prostopadle do siebie. Trójkąt zbudowany z tych wektorów wyznacza ich wypadkową. Dodawane wektory należy rysować tak, by grot jednej strzałki łączył się z końcem drugiej. Siła wypadkowa biegnie od końca jednej strzałki do grotu drugiej.




Równoległobok wektorów

Innym sposobem znajdowania dwóch sił 3 N i 4 N zaczepionych w jednym punkcie i działających prostopadle do siebie jest zastosowanie reguły równoległoboku. Wektory te stanowią dwa boki prostokąta. Przekątna przechodząca przez punkt O określa wartość i kierunek wypadkowej.

Metodę tę można stosować również do dodawania wektorów, które nie są do siebie prostopadłe.





Wartość wypadkowej zależy od ustawienia dodawanych wektorów względem siebie. Wartość wypadkowa tylko zastępuje dwa inne wektory. Nie są to trzy działające wektory.

c) Realizacja tematu: Wektor położenia.

Ruch jest jednym z podstawowych pojęć w fizyce. Każdy z nas potrafi wskazać ciała, które się poruszają i które pozostają w spoczynku. To czy jakieś ciało porusza się czy nie, zależy od wyboru układu odniesienia. Weźmy na przykład jazdę pociągiem. Biorąc pod uwagę stację jesteśmy w ruchu, choć tak naprawdę siedzimy w przedziale i względem siedzenia jesteśmy w spoczynku.

Każdy ruch jest względny, gdyż wymaga przyjęcia układu odniesienia. Ciała poruszają się zawsze względem wybranego układu. Obserwator na Ziemi przyjmuje najczęściej układ odniesienia związany z przedmiotami znajdującymi się na powierzchni Ziemi. Prawidłowego opisu ruchu możemy dokonać dobierając dowolny układ odniesienia.

W celu dokładnego określenia ruchu przyjmujemy układ odniesienia składający się z trzech prostopadłych do siebie osi O_x, O_y, O_z. W układzie tym za pomocą współrzędnych x, y, z można wyznaczyć położenie dowolnego punktu w przestrzeni. Położenie można wskazać także za pomocą wektora łączącego początek układu (punkt O)z danym punktem M. Wektor ten nazywamy wektorem położenia lub wektorem wodzącym i oznaczamy OM = r




Do określenia położenia punktu na płaszczyźnie potrzebne są tylko dwie współrzędne, np. x (odcięta) i y (rzędna). I służy do tego prostokątny układ współrzędnych nieruchomy względem ciał wybranych jako układ odniesienia. Wektor OA = r₁ określa położenie ciała w punkcie A. Zapis r₁ =(x,y) oznacza, że wektor r₁ ma współrzędne x i y. Znając je można łatwo obliczyć długość wektora, czyli odległość przemieszczającego się punktu od początku układu współrzędnych, korzystając z Twierdzenia Pitagorasa:




Dla każdego wektora pierwiastek z sumy kwadratów współrzędnych nazywamy wartością wektora. Podanie współrzędnych x i y wektora położenia nie jest jedynym sposobem zdefiniowania położenia. Równie dobrze można podać samą wartość r tego wektora oraz kąt skierowany α jaki tworzy ten wektor z dodatnią częścią osi odciętych.

Gdy punkt się porusza i pod wpływem swego ruchu przejdzie z punktu A do punktu B , zajmie nowe położenie, które określimy wektorem r₂. Wektor łączący A z B czyli AB = Δr nazywamy wektorem przemieszczenia. Stosując rachunek wektorowy poznany na poprzednich lekcjach, otrzymujemy wektor przemieszczenia Δr, który jest różnicą wektorów położeń r₂ i r₁. Jest to wektorowy zapis ruchu. Δr = r₂ - r₁

W miarę upływu czasu koniec wektora położenia zakreśla na płaszczyźnie linię, która nazywa się torem ruchu. Kształt toru zależy od wyboru układu odniesienia.

Jeżeli wektor wodzący danego punktu, określający położenie w układzie odniesienia ulega zmianie, to punkt ten jest w ruchu względem tego układu.

Wektor ten ulega zmianie, gdy zmienia się jego kierunek (czyli prosta, na której leży), zwrot lub wartość (długość wektora). Wszystkie te wielkości mogą ulegać zmianie niezależnie od siebie.

Ze składaniem ruchów jednostajnych możemy mieć do czynienia analizując ruch człowieka jadącego pociągiem po szynach (ruch w kierunku x) i jednocześnie podnoszącego torbę (ruch w kierunku y). Podobnie przedstawia się sytuacja , gdy pływak przeprawia się przez spokojnie płynącą rzekę, prostopadle do jej brzegu. Prąd wody znosi go (ruch wzdłuż osi x), nie wpływając praktycznie na ruch w kierunku prostopadłym do nurtu rzeki (ruch wzdłuż osi y).

Zadania:

1. Po prostym odcinku przemieszcza się pociąg. Początek układu odniesienia przyjmij w jakimś punkcie. Przeanalizuj i opisz jak zmienia się ruch siedzącego w nim człowieka, gdy za układ odniesienia przyjmiemy tory, a gdy pewną stację.

2. Dziecko siedzi na krzesełku karuzeli. Przyjmij układ odniesienia w środku karuzeli i przeanalizuj jego ruch.

3. Oblicz długość wektora r określającego położenie ciała w punkcie A o współrzędnych (3,4).

4. Oblicz przemieszczenie Δr ciała z punktu A, którego wektor wodzący ma długość r₁ = 4 cm do punktu B o r₂ = 8 cm.




---