Rok akademicki 2006/2007 |
Laboratorium Fizyki |
|||
Nr ćwiczenia: 50 |
Pochłanianie światła |
|||
Wydział: WBiIŚ Kierunek: IŚ Grupa: OCiK lab. 3 |
Hanna Spierewka |
|||
Data wykonania |
Ocena |
Data zaliczenia |
Podpis |
|
14.11.2006 r. |
Teoria |
|
|
|
|
Sprawozdanie |
|
|
|
Zasada pomiaru
Celem ćwiczenia było wyznaczenie zależności współczynnika absorpcji światła od długości fali (krzywej absorpcji) dla barwnych szkieł przy pomocy jednowiązkowego spektrofotometru fotoelektrycznego spekol.
Absorpcją światła, czyli pochłanianiem, nazywamy straty energii strumienia światła, występujące przy przechodzeniu tego strumienia przez ośrodek materialny, w którym to światło nie ulega rozproszeniu. Straty strumienia świetlnego w substancji są wynikiem przemiany energii strumienia świetlnego w różne rodzaje energii wewnętrznej substancji (np. ciepło, jonizacja) oraz w energię promieniowania wtórnego, wysyłanego w innych kierunkach lub mającego inny skład widmowy.
Gdy przez warstwę dx jednorodnego, przezroczystego ośrodka przechodzi w kierunku x wiązka światła monochromatycznego, to osłabienie strumienia świetlnego dΦ na drodze dx jest proporcjonalne do wartości tego strumienia i grubości warstwy.
![]()
a więc,
![]()
(1)
gdzie k - współczynnik absorpcji, jest wielkością charakteryzującą absorpcyjne własności ośrodka.
Jeśli strumień światła przechodzi przez warstwę o skończonej grubości l i zmienia się od wartości początkowej Φ0 do wartości końcowej Φl , to całkując równanie różniczkowe (1) w tych granicach otrzymamy:
lnΦl - lnΦ0 = - k⋅l (2)
czyli
![]()
(3)
Zależność tę nazywamy prawem Lamberta - Beera. Sens fizyczny współczynnika absorpcji k wynika bezpośrednio ze wzoru (3).
Dla
![]()
Zatem odwrotność współczynnika absorpcji k określa taką drogę w ośrodku, po przejściu której strumień światła zmaleje e razy.
W układzie współrzędnych logarytmicznych równanie (2) przedstawia linię prostą.
Stosunek ![]()
nazywany jest transmisją T.
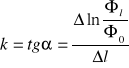
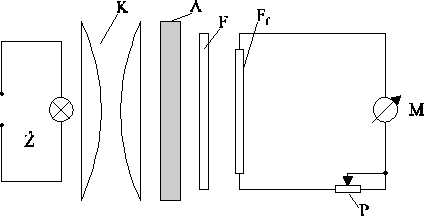
Schemat układu pomiarowego
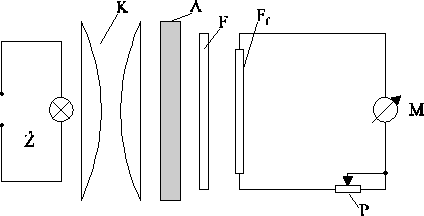
Kolorymetr użyty w pomiarach składa się ze źródła światła Ź, kondensatora K, filtru selektywnego F (komplet filtrów), fotodiody lub fotoogniwa Ff, połączonego z miernikiem M przez potencjometr P. Badane płytki szklane A umieszcza się na drodze wiązki światła w specjalnej komorze, prostopadle do wiązki. Miernik kolorymetru ma dwie skale - skalę transmisji i absorpcji. Skala transmisji podaje w procentach wartość stosunku
![]()
gdy bez absorbenta strumień Φ0 spowoduje pełne wychylenie wskazówki miernika (100%). Do regulacji tego wskaźnika służy potencjometr P.
Ocena dokładności pojedynczych pomiarów
W doświadczeniu użyto:
1. Kolorymetr do pomiaru transmisji T ΔT = 0.5%
ΔT = 0,005
2. Śruba mikrometryczna do pomiaru d Δd = 0.01 [mm]
Tabele pomiarowe
Płytki przezroczyste
Grubości płytek użytych do pomiarów
1,24 [mm]
1,26 [mm]
1,25 [mm]
1,22 [mm]
1,26 [mm]
1,24 [mm]
1,22 [mm]
Długość fali [nm] |
1d |
2d |
3d |
4d |
5d |
6d |
7d |
|
T lnT |
T lnT |
T lnT |
T lnT |
T lnT |
T lnT |
T lnT |
750 |
0,89 -0,12 |
0,81 -0,21 |
0,73 -0,31 |
0,66 -0,41 |
0,59 -0,53 |
0,53 -0,63 |
0,48 -0,73 |
700 |
0,89 -0,12 |
0,81 -0,21 |
0,73 -0,31 |
0,66 -0,41 |
0,60 -0,51 |
0,54 -0,62 |
0,50 -0,69 |
620 |
0,88 -0,13 |
0,78 -0,25 |
0,71 -0,34 |
0,64 -0,45 |
0,58 -0,54 |
0,52 -0,65 |
0,45 -0,80 |
570 |
0,89 -0,13 |
0,80 -0,22 |
0,73 -0,31 |
0,65 -0,43 |
0,61 -0,49 |
0,55 -0,60 |
0,50 -0,69 |
500 |
0,90 -0,10 |
0,81 -0,21 |
0,74 -0,30 |
0,67 -0,40 |
0,61 -0,49 |
0,55 -0,60 |
0,50 -0,69 |
450 |
0,90 -0,10 |
0,79 -0,24 |
0,72 -0,33 |
0,67 -0,40 |
0,60 -0,51 |
0,54 -0,62 |
0,50 -0,69 |
Płytki brązowe
Grubości płytek użytych do pomiarów
2,15 [mm]
2,25 [mm]
2,22 [mm]
2,22 [mm]
2,15 [mm]
Długość fali [nm] |
1d |
2d |
3d |
4d |
5d |
|
T lnT |
T lnT |
T lnT |
T lnT |
T lnT |
750 |
0,72 -0,33 |
0,52 -0,65 |
0,38 -0,97 |
0,28 -1,27 |
0,22 -1,51 |
700 |
0,69 -0,37 |
0,50 -0,69 |
0,34 -1,08 |
0,24 -1,43 |
0,19 -1,66 |
620 |
0,55 -0,60 |
0,33 -1,11 |
0,21 -1,56 |
0,11 -2,21 |
0,07 -2,66 |
570 |
0,38 -0,97 |
0,16 -1,83 |
0,07 -2,66 |
0,03 -3,51 |
0,01 -4,60 |
500 |
0,11 -2,21 |
0,01 -4,60 |
|
|
|
450 |
0,03 -3,51 |
|
|
||
Przykładowe obliczenia wyniku pomiarów wielkości złożonej
- obliczenie współczynnika absorpcji ze wzoru:
![]()
Przykładowe obliczenie współczynnika k dla pomiaru nr 1 z tabeli 1:
![]()
Zestawienie współczynników k
Długość fali [nm] |
Przezroczyste |
Brązowe |
750 |
0,08 |
0,13 |
700 |
0,08 |
0,15 |
620 |
0,09 |
0,23 |
570 |
0,07 |
0,41 |
500 |
0,08 |
1,06 |
450 |
0,08 |
|
Rachunek błędów
Błąd współczynnika absorpcji obliczono metodą różniczki zupełnej

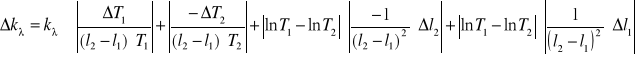
przy czym: l1, l2 - grubości płytek
Δl1, Δl2 - błędy pomiaru grubości płytek
- Przykładowe obliczenie dla danych zawartych w tabeli 1, pozycja nr 1:
ΔT1 = ΔT2 = 0,005
T1 = 89% = 0,89 T2 = 48% = 0,48
lnT1 = - 0,12 lnT2 = - 0,73
d1 = 1,24 [mm] d2 = 8,69 [mm]
Δd1 =0,01[mm] Δd2 = 0,07 [mm]
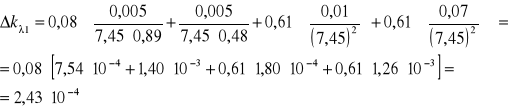
Tabela błędów współczynnika
|
Przezroczysta |
Brązowa |
|
Δkλ1 |
2,43 ⋅10-4 |
6,52⋅10-4 |
|
Δkλ2 |
2,33⋅10-4 |
8,43⋅10-4 |
|
Δkλ3 |
2,90⋅10-4 |
2,76⋅10-3 |
|
Δkλ4 |
2,03⋅10-4 |
0,03 |
|
Δkλ5 |
2,35⋅10-4 |
0,27 |
|
Δkλ6 |
2,35⋅10-4 |
- |
|
Zestawienie wyników pomiarów
|
Przezroczysta |
Brązowa |
|
kλ1 |
(80,00 ± 0,24) ⋅ 10-3 |
(130,00 ± 0,65) ⋅ 10-3 |
|
kλ2 |
(80,00 ± 0.23) ⋅ 10-3 |
(150,00 ± 0,843) ⋅ 10-3 |
|
kλ3 |
(90,00 ± 0,29) ⋅ 10-3 |
(230,00 ± 2,76) ⋅ 10-3 |
|
kλ4 |
(70,00 ± 0,20) ⋅ 10-3 |
0,41 ± 0,03 |
|
kλ5 |
(80,00 ± 0,23) ⋅ 10-3 |
1,06 ± 0,27 |
|
kλ6 |
(80,00 ± 0,23) ⋅ 10-3 |
- |
|
Uwagi i wnioski
Decydujący wpływ na pomiary mogły mieć niedokładności w umieszczeniu płytek
w spektrometrze, jak również zabrudzenia i nieznaczne pęknięcia płytek.
Wyszukiwarka
Podobne podstrony:
Sprawozdanie fiza 5 (ćw.71), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
ĆW-68-~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Sprawozdanie fizyka 4, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, Fizyka
CW 7211, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, fizyka1, fiza, Fizyka 2, 72(dodatk
WYKRES73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizzad2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
STOS-EM, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizyka21, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizWyks2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
065S~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizPrad, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
051C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
SUCHY73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
062C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
więcej podobnych podstron