Sprawozdanie pobrano z http://www.studentsite.pl
Chcesz pobrać więcej sprawozdań? Wejdź na http://www.studentsite.pl/materialy_studenckie
1.Wytrz.mat.-dziedzina wiedzy inżynierskiej,część mechaniki technicznej zajmująca się opisem zjawisk zachodzących w mat.konstrukcyjnych poddanych zew. obciążeniom. Wytrzymałość to nauka o odkształceniach i naprężeniach. 2.Wytrz.mat.to dział mechaniki zajmujący się ciałami odkształcalnymi.Obejmuje teoretyczne i doświadczalne badania procesów odkształcania i niszczenia ciał poddanych różnorodnym obciążeniom.Prowadzi do analizy zachowania się konstrukcji pod działaniem obciążeń.Pozwala to zaprojektować konstrukcję tak,aby mogła poprawnie pracować tworząc jednocześnie układ racjonalnie zaprojektowany.W ogólnym przypadku wytrz.mat.zajmuje się obserwowaniem zachowania się ciała poddanego siłom zew.pod kątem odpowiadającym im siłom wew.i odpowiadającym im naprężeń oraz wywołanych przez nie odkształceń
3. Stal St 35, stal sprężynowa 60 SGH, żeliwo zwykłe, aluminium, cyna, cynk, ołów, miedź, wolfram, stop Al.-Cu D16, stop Cu-Sn (brąz), sosna i dąb (wzdłuż włókien), beton,szkło potasowe, kauczuk miękki
4. Założenie sprężystości liniowej (materia wypełnia w sposób ciągły dowolną część ciała), założenie jednorodności materiału (własności materiału we wszystkich punktach są jednakowe), założenie izotropii materiału (materiał wykazuje jednakowe własności mechaniczne we wszystkich kierunkach), założenie niezależności działania sił (skutek działania na ciało ukł.sił jest sumą skutków działania poszczególnych sił,przykładanych w dowolnej kolejności)
5.Odkształcenie-zmiana wymiaru w stosunku do wymiaru początkowego (zmiana długości).Dzielimy na:bezwzględne Δl=l - l0 [mm], względne ε =Δl / l0.Ponad to mamy odkszt.kątowe,liniowe oraz ściskanie, rozciąganie,ścinanie,skręcanie,zginanie 6.Naprężenie-siła wew.wywołana przez obciążenie zew.przypadające na jednostkę pow.Dzielimy na naprężenia: całkowite,normalne,styczne
7.Równania konstytutywne są związkami materiałowymi,definiującymi materiał.W procesach mech.takimi związkami są zależność pomiędzy tensorem naprężenia a miarami deformacji (odkształcenia).Równ.konstytutywnym ciał liniowo sprężystych jest prawo Hookea.Ogólna charakterystyka: nie wynikają z ogólnych zasad termodynamiki,mają charakter postulatywny,nie ma uniwersalnych zasad konstruowania zasad konstutatywnych, teoria tych równań jest w ciągłym rozwoju i jest uzupełniana
8. Zależność pomiędzy napręż.a odkszt.formułuje prawo Hookea,które głosi że odkształcenie ciała pod wpływem działającej nań siły jest wprost proporcjonalne do tej siły. Trójosiowy stan napręż. σz= Łmax= ½ (σ1-σ3)-<kr
Oznacza to, że naprężenie σ1 może być większe od granicy plastyczności, zanim powstanie w materiale krytyczny stan zapoczątkowujący jego płynięcie. Hipoteza daje wyniki najbardziej zgodne z doświadczeniem dla materiałów plastycznych stale niskowęglowe).
9..Rodzaje obciążeń
Jednym z podstawowych zadań elementów konstrukcyjnych jest zrównoważenie obciążeń
zewnętrznych lub wykonanie określonej pracy, sprowadzonej do przemieszczania w kierunkachwyznaczonych działaniem działających sił. W tym rozumieniu obciążenia zewnętrzne są równeciężarowi własnemu konstrukcji, obciążeniom użytkowym oraz wpływom zewnętrznym związanym z użytkowaniem urządzenia. Zwykle obciążenia działające na konstrukcję dzielimy na:
• Obciazenia stale. Do obciążeń tych zalicza się ciężar własny konstrukcji oraz ciężar własnyelementów podtrzymywanych przez konstrukcję. Obciążenie to w okresie eksploatacji naniezmienną wartość.
• Obciazenia uzytkowe (zmienne). Jest to grupa zasadniczych obciążeń, dla których projektuje się
daną konstrukcję. Do obciążeń tych należą m.in.: obciążenia od wyposażenia technologicznego,
siły bezwładności wynikające z pracy urządzeń, wpływ prędkości odkształceń, wpływ czasu
obciążenia, wpływ obciążeń wielokrotnych. Zakres tych obciążeń jest bardzo szeroki a ich
oszacowanie należy do najbardziej istotnych fragmentów budowy modelu statycznego.
• Wplyw otoczenia. Grupa warunków pracy konstrukcji obejmująca wpływy atmosferyczne (śnieg,
wiatr), wpływ temperatury otoczenia, napromieniowanie itp. Zwykle zakres tych wpływów
określają odpowiednie normy, ale może zachodzić potrzeba indywidualnej analizy, szczególnie w
przypadku konstrukcji prototypowych.
• Obciazenia transportowe i montazowe. Są to obciążenia określające zachowanie się elementu lub
konstrukcji w czasie transportu i montażu, gdy elementy nie są jeszcze całkowicie złączone
zgodnie z ich udziałem w maszynie lub urządzeniu.
Oczywiste jest przy tym, że w trakcie analizy ze zbioru możliwych kombinacji obciążeń należy
uwzględniać zestawy obciążeń wywołujące najbardziej niekorzystne układy sił i momentów zarówno
elementów składowych jak i całej konstrukcji.
10..Zasada de Saint-Venanta
Równowazne uklady sil dzialajace na maly obszar ciala wywoluja takie same stany naprezenia w
calym ciele z wyjatkiem bezposredniego otoczenia przylozonych sil.
Spiętrzenia naprężeń w miejscach styku dociskanych wzajemnie ciał są rozpatrywane jako
osobne zagadnienie naprężeń powierzchniowych (wytrzymałości kontaktowej) w odróżnieniu od
naprężeń występujących w całej objętości rozpatrywanych ciał.
Jeżeli na pewny niewielki obszar ciala sprężystego działają kolejno rozmaicie rozmieszczone ale statycznie równowarte obciążenia to w odległości od obszaru dużo większej niż ego wymiary powstaja praktycznie jednakowe stany naprężenia i odkształcenia jest to zasada sprężystej równoważności statycznie równoważnych układów sił.
Zasada mówi, że jeśli na sprężyste ciało działa układ sił statycznych to w przekroju tego ciała znacznie odległym od punktów przyłożenia tych sił, ich wpływ się uśrednia.
Ilustracją zasady jest rysunek. Pokazuje on pręt rozciągany przez parę sił przyłożonych punktowo na obu końcach. W bezpośredniej bliskości końców stan naprężenia odpowiada rzeczywistemu stanowi obciążenia. W dostatecznej odległości od końców uśrednia się i równy jest sumie sił podzielonej przez pole przekroju pręta.
11.jednorodność
takie same właściwości materiału w każdym punkcie
izotropia niezależność właściwości mechanicznych (jak np. moduł Younga) od kierunku; dla ciał izotropowych, fizykalnie liniowych, kierunki główne naprężeń i odkształceń pokrywają się a liczba stałych materiałowych redukuje się do 2.
12.stała materiałowa
wielkość charakterystyczna dla materiału; dla ciała izotropowego tylko dwie stałe są niezależne
13 Liniowa sprezystosc mat. Polega na tym ze proces odksztalcenia sprezystego i odciazenie jest odwracalne.
14 Wymien podstawowe stale materiałowe dla materialu liniowo sprężystego -wydluzalnosc As -granica sprężystości Rc -modul Kirhoffa G -modul Yanga E 15. Podaj definicje: momentow statycznych przekroju oraz promieni bezwładności Moment statyczny pola przekroju względem dowolnej osi rowny iloczynowi pola tego przekroju i wspolzednej srodka ciężkości tego pola przekroju względem danej osi . Moment statyczny dowolnej figury względem osi przechodzącej przez srodek ciężkości tej figury jest rowny zeru. Moment bezwładności-pierwiastek kwadratowy z ilorazu momentu bezwładności i powierzchni przekroju , odległość od osi na jakiej należy skupic cala mase przekroju aby moment bezwl. Względem tej osi był taki sam jak dla rzeczywistego przekroju
17.Biegunowy moment bezwładności przekroju (tylko kołowego lub pierścieniowego) belki jest parametrem przekroju opisującym wytrzymałość na skręcanie. Gdy przemnożymy biegunowy moment przekroju razy moduł Kirchhoffa to otrzymamy sztywność na skręcanie belki. Patrz: Skręcanie (wytrzymałość materiałów) (dla przekrojów kołowych IS = IO).
.Moment bezwładności przekroju po angielsku jest zwany Second moment of area.
Moment bezwładności figury płaskiej ma wymiar długość^4 (w SI m^4).
Biegunowy moment bezwładności to moment bezwładności względem punktu będącego środkiem ciężkości. Definicja:
Moment bezwładności to miara bezwładności ciała w ruchu obrotowym. Im większy moment tym trudniej rozkręcić dane ciało lub zmniejszyć jego prędkość obrotową.
gdzie:
m - masa fragmentów ciała oddalonych od osi obrotu o długość r
r - odległość fragmentów ciała od jego osi obrotu
czynnik jest sumą iloczynów mas cząstek przez kwadraty ich odległości od osi obrotu. Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od sposobu rozmieszczenia masy ciała. Moment bezwładności ma wymiar ML2. Zwykle mierzy się go w kgm2 .Posługując się pojęciem momentu bezwładności można wyrazić energię kinetyczną obracającego się ciała sztywnego w postaci.
21Skutkiem dzialania sily normalnej jest odksztalcenie preta przejawiajace sie w przemieszczeniu przekroju wzdluz kierunku dzialania sily.Przekroje preta po odksztalceniu pozostaja plaskie i prostopadle do jego osi.
22.εp=-νε, υ=εn/εm, ε-odkształcenie, n-dowolny kierunek prostopadły do -m
23.Δl=l-lo, Δl=F*lo/A*E
24Stan naprezenia w przekrojach , w ktorych wystepuja tylko naprezenia styczne nazywamy czystym scinaniem.W elementach konstrukcyjnych spotykanych w technice można znalezc takie przekroje w ktorych wystepuja czyste scinanie np. Podczas czystego skrecania.Przewaznie w przekrojach elementow konstrukcyjnych wystepuja jednoczesnie naprezenia normalne i styczne.Scinaniem technologicznym nazywamy naprezenia i odksztalcenia mat. Spowodowane 2 silami tworzacymi pare o bardzo malym ramieniu.
25a)czy nie zostalo przekroczone dopuszczalne naprezenie rozciagajace dla mat. Czesci laczonych,b)czy nie zostalo przekroczone dopuszczalne naprezenia scinajace dla mat nitow,c)czy nie zostalo przekroczone naciski dopuszczalne dla mat nitow*wytrzymalosc nitow na scinanie ma byc mniejsza od wytrzymalosci blach na naciski powierzchniowe. d./g=3,2/m d-średnica otworu litowego, g- gr. Blachy, m- liczba ścinanych przekrojów w 1 nicie
26. Ścinanie spoiny pow. τ=F/S≤kt S-pole przekroju spoiny kt-dopuszczalne napręzenie na ścinanie, pole przekroju S=a*l, a- grubość spoiny, całkowita długość spoiny pow. L=F/kt*a,
27. Kąt skręcania wału jest proporcjonalny do momentu skręcającego i długości wału a odwrotnie proporcjonalny do modułu Kirchoffa i momentu bezwładności =Ms*l/G*I0
-kąt skręcania (rad) I0-moment bezwład G-moment Kirchoffa
28. Wzór na moment bezwładności na skręcanie I0=d4/32
29. rozkład naprężeń przy skręcaniu -wartość naprężeń stycznych r zwieksza się proporcjonalnie do odległości od osi wału poczynając od 0 w jego środku do wartości max we włóknach skrajnych -naprężenia r są styczne do odpowiednich okręgów przekroju, czyli są prostopadłe do odpowiednich promieni -elementy siły styczne dt p=rp*dA τmax=Ms/W0≤ks
W0-wskaźnik wytrzymałości na skręcanie Ms- moment skręcający ks- naprężenia dopuszczalne przy skrecaniu
30.Podaj warunki projektowania przekroju przy skręcaniu
*τmax= 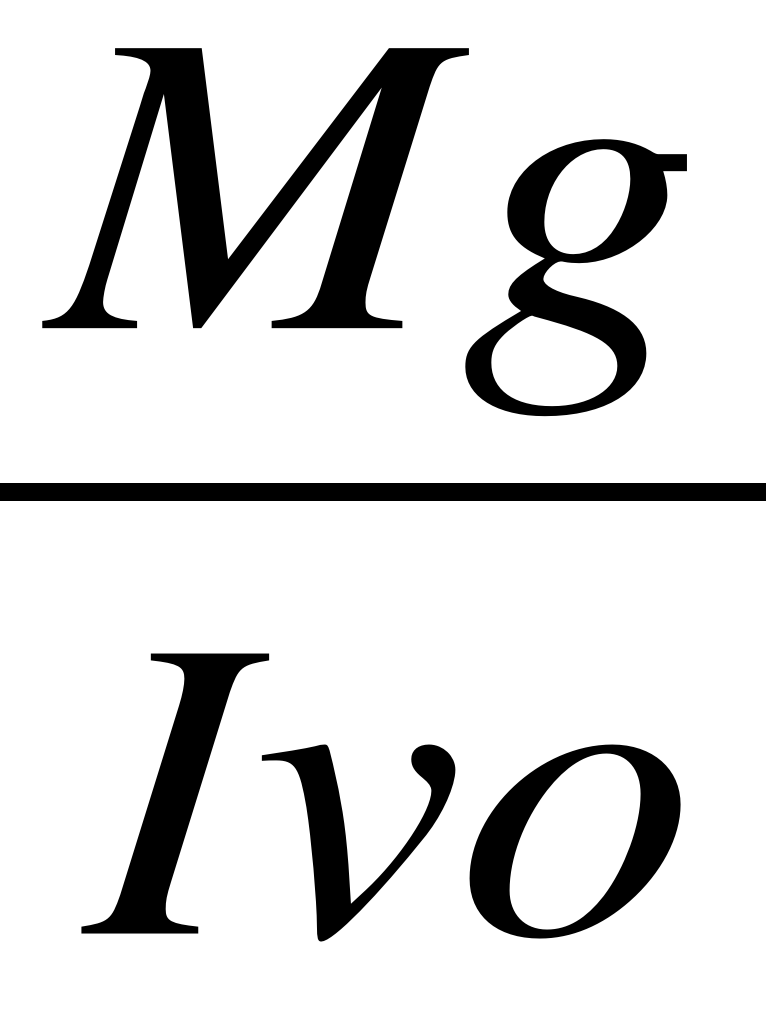
\ Ks (naprężenia dopuszczalne na skrecanie)
*warunek odkształceniowy Cpmax=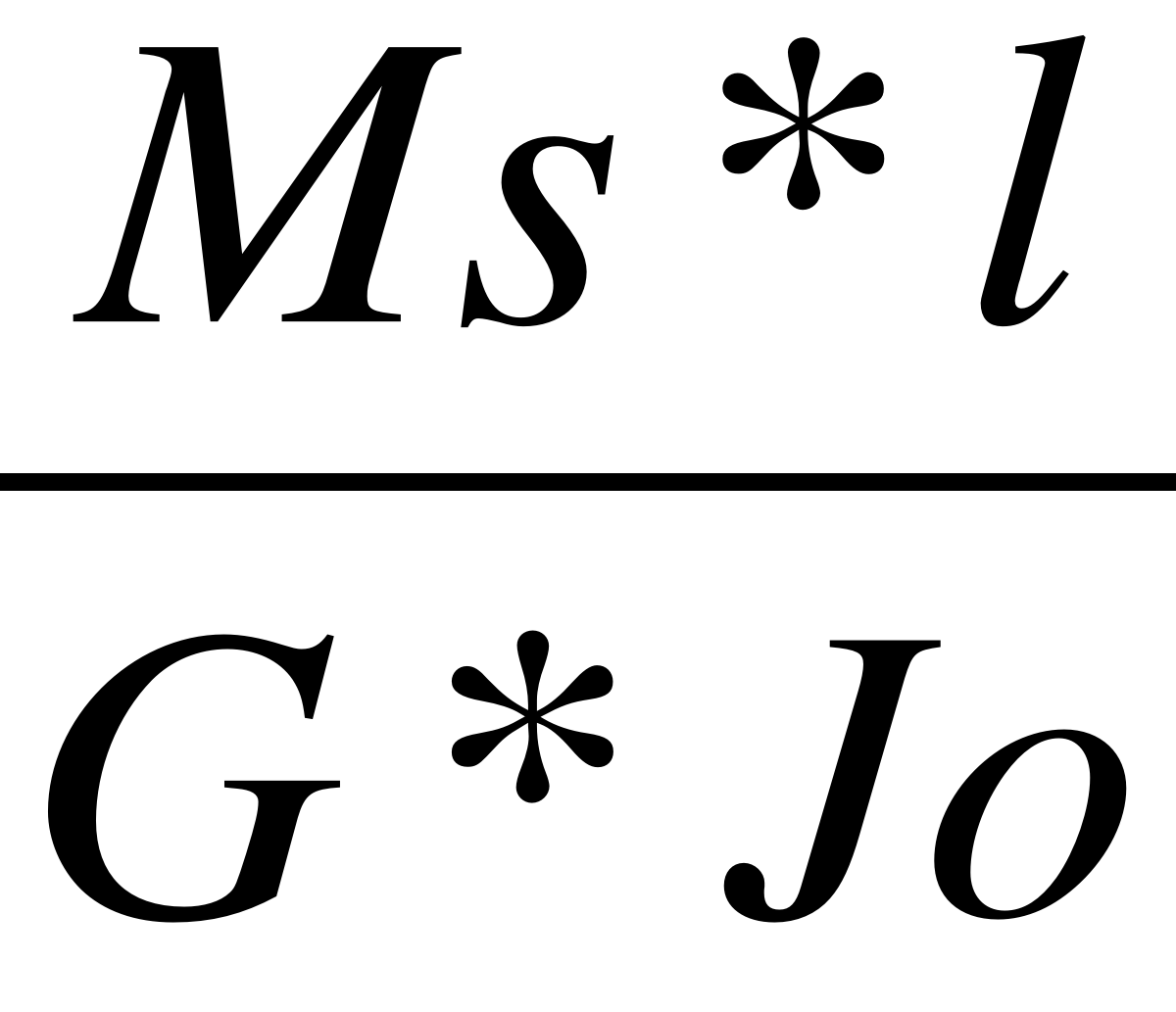
\ Cpdop (najweikszy dopuszczony kąt skrcania)
31. podaj def kata skrecania i jednostkowego kąta skrecania -kąt skrecania jest proporcjonalny =Ms*l/G*I0 Ms- moment skręcający l-długośc I0-biegunowy moment bezwladnosci G-moment Kirchoffa
32. Stan naprężenia i rozkład naprężeń przy skrecaniu -w określonym punkcie ciała rozumiemy ogół naprężeń otrzymanych dla wszelkich możliwych przekrojów przechodzących przez punkt. (Cd 29)
33.Moment bezwładności na skrecanie- We wzorach dotyczących wytrzymałości materiałów wykorzystywane są statyczne momenty powierzchniowe wyższego rzędu które przez analogię do pojec znanych ze statyki nazywamy momentami bezwładności pow. Miarą bezwładności sa m4
34.Scharakteryzuj stan naprężenia przy czystym zginaniu.
Przez stan naprężenia w pkt. ciała rozumie się zbiór naprężeń występujących w tym
pkt. na dowolnych przezeń poprowadzonych przekrojach. Stan naprężenia w pkt ciała uważa
się za określony,gdy można wyznaczyć wektor naprężenia całkowitego w tym pkt na dowolnie
nachylonym przekroju,poprowadzonym przez ten pkt. czystym zginaniem(zginaniem równomiernym)
nazywa sie taki przypadek wytrzymałościowy, w którym w przekroju poprzecznym pryzmatycznego
pręta prostego wystąpi tylko moment zginający(pozostał siły wew powinny być równe
0)
35.Wzór na naprężenie przy czystym zginaniu
Czyste zginanie dzielimy:a)zginanie równomierne proste(strefa rozciągania,warstwa włókien
obojętnych,strefa ściskania. w przypadku zginania równomiernego prostego występuje tylko
naprężenie normalne, działające wzdłuż pręta,WZOR!!!b)zginanie równomierne ukośne(wartość
naprężenia normalnego w pkt A utrzymuje się sumując algebraicznie wyniki cząstkowe)
36.Określ rozkład naprężeń normalnych w przekroju poprzecznym przy czystym zginaniu
Z przeprowadzonej relacji wynika, że w przypadku zginania równomiernego prostego rozkład
naprężeń normalnych na wysokości przekroju jest liniowy. Największe naprężenia co do
wartości bezwzględnej wystąpią w pkt przekroju najdalej odsuniętych od linii obojętnej
Dla wszystkich pkt leżących w przekroju na linii obojętnej otrzymuje się sigma=0
37.Opisz położenie osi obojętnej przy czystym zginaniu
Miejsce geometryczne punktów przekroju, w których znikają naprężenia nazywa sie osią
obojętną. W przypadku zginania bez udziału innych uogólnionych wielkości wew nazywanego
zginaniem czystym, os obojętna przechodzi przez środek geometryczny przekroju. Jeżeli oś
obojętna jest prostopadła do płaszczyzny pary sił zginających wówczas mamy do czynienia
ze zginaniem prostym Rys!!!!
38.Gdzie występuje największe naprężenie w przekroju przy czystym zginaniu?
Największe naprężenie co do wartości bezwzględnej występuje w pkt przekroju
najdalej odsuniętych od linii obojętnej. Dla wszystkich punktów leżących w przekroju nalinii obojętnej otrzymuje sie sigma=0
39.Scharakteryzuj stan odkształcenia przy czystym zginaniu.
stan odkształcenia może być:trójosiowy(przestrzenny)różnymi od 0 są wszystkie 3
wydłużenia główne,dwuosiowy(płaski)różnymi od 0 sa 2 wydłużenia główne,jednoosiowy
(liniowy)różnym od 0 jest jedno wydłużenie główne. Pod działaniem obciążenia a także innych przyczyn(zmiana temp,skurcz)ciało odkształca się. Odkształcenia polegają na zmianach długości i zmianach katów. Elementarny prostopadłościan zawierający rozpatrywany punkt ciała przechodzi na ogół w równoległościan przy czym długości boków i kąty między nimi zmieniają się. W każdym punkcie ciała można wyznaczyć 3 wzajemne prostopadłe kierunki główne:1,2,3 takie że odpowiadający im elementarny prostopadłościan nie dozna odkształceń kątowych a dozna jedynie odkształceń liniowych E1,E2,E3 zwanych wydłużeniami głównymi.
40.Co wiesz o deformacji przekroju poprzecznego przy czystym zginaniu?
Do rozważań przyjęto pręt pryzmatyczny. Obciążenie momentem spowoduje,że pręt uprzednio prosty ulegnie deformacji. Jeżeli założy się umownie,że na ramach pojęcia ciągłości materialnej struktura pręta jest włóknista to można stwierdzić że po deformacji włókna górne będą rozciągane zaś dolne ściskane. Skoro włókna górne w pręcie są rozciągalne a dolne ściskane to przy ciągłości
rozkładu skutków musi istnieć na wysokości\ warstwa włókien , które nie będą rozciągane ani też ściskane nazywa sie je włóknami obojętnymi (warstwa obojętna)
41.Co to jest wskaźnik wytrzymałości?
Wz=Iz/e Iz moment bezwładności przekroju względem osi z. E-odległość punktów skrajnych od osi obojętnej. Jest to iloraz momentu bezwładności i przekroju względem osi obojętnej i odległości skrajnych włókien od tej osi.
42..jaki przekrój najlepiej pracuje na zginanie? Dwuteownik.
- Dwuteownik - kształtownik walcowany o przekroju poprzecznym zbliżonym do dwóch liter T, połączonych podstawami. W zależności od szerokości stopki w stosunku do wysokości środnika, dwuteownik dzieli się na zwykłe, szeroko stopowe, niskie.
Ze względu na dużą wytrzymałość na zginanie dwuteownika stosuje się na konstrukcje nośne budynków przemysłowych (hal i wiat fabrycznych i magazynowych), konstrukcje dźwignic, w kolejnictwie itp.
Wyszukiwarka
Podobne podstrony:
sciaga drogi 2, NAUKA, budownictwo nowe 4.12.2011, Budownictwo komunikacyjne
sciaga drogi, NAUKA, budownictwo nowe 4.12.2011, Budownictwo komunikacyjne
sciaga test z drogi 2007, NAUKA, budownictwo nowe 4.12.2011, Budownictwo komunikacyjne
sciaga drogi 2, NAUKA, budownictwo nowe 4.12.2011, Budownictwo komunikacyjne
Materialy Budowlane-3R, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
FOLIE MIESZANKA BETON, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
METODA 3 RÓWNAŃ- wzorki, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
Drogi TEST, NAUKA, budownictwo nowe 4.12.2011, Budownictwo komunikacyjne
Beton CAŁY, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
Beton, NAUKA, budownictwo nowe 4.12.2011, a) RÓŻNE
Otulenie ziaren kruszywa zaczynem cementowym, NAUKA, budownictwo nowe 4.12.2011, a) RÓŻNE
materialy budowlane, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
Ile wynosi wartość pochylenia poprzecznego nawierzchni na prostej, NAUKA, budownictwo nowe 4.12.2011
Kopia BADANIA MIESZANKI BETONOWEJ, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
Przykład projektowania betonu, NAUKA, budownictwo nowe 4.12.2011, a) RÓŻNE
Projektowanie betonu, NAUKA, budownictwo nowe 4.12.2011, a) RÓŻNE
DO WYDRUKOWANIA NA ZAJĘCIA, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
TB - opracowane, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
Materialy Budowlane-3R, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
więcej podobnych podstron