Pracownia Zakładu Fizyki Politechniki Lubelskiej

Nazwisko						Wydział Elektryczny Grupa EdI 2.1.
Data wyk. ćwicz.: 1998-03-05		Numer ćwiczenia: OP.1.1		Temat ćwiczenia: Wyznaczanie współ. załamania światła z pomiarów kąta załamania oraz kąta granicznego
	ZALICZENIE		Ocena		Data		Podpis

1. WYNIKI POMIARÓW I OBLICZEŃ

a). Tabelka

Próbka nr 1
Lp	α	α	β	β	n	γ	n (zγ)	n
	^0	^rad	^0	^rad		^0
1	3	0.052	3	0.052	1.00	43.5	1.45	1.38
2	5	0.087	4.5	0.079	1.11
3	7	0.122	6	0.105	1.17
4	10	0.174	8	0.140	1.25
5	12	0.209	9	0.157	1.33
6	15	0.262	11.5	0.201	1.30
7	17	0.297	13	0.227	1.30
8	20	0.349	15	0.262	1.32
9	22	0.384	16	0.279	1.36
10	25	0.436	18	0.314	1.37
11	28	0.488	20	0.349	1.37
12	30	0.523	21	0.366	1.40
13	32	0.558	22.5	0.393	1.38
14	35	0.611	24	0.419	1.41
15	40	0.698	27	0.471	1.42
16	45	0.785	30	0.523	1.41
17	50	0.872	32	0.558	1.45
18	55	0.959	35	0.611	1.43
19	60	1.047	37	0.645	1.44
20	65	1.134	39	0.680	1.44
21	70	1.221	41	0.715	1.43
22	75	1.308	42	0.733	1.44

b). Przykładowe obliczenie wyników:

dokładność tarczy - 0.5 ⁰ - 0,0087 rad

Zgodnie z zaleceniem (skrypt "Optyka") w obliczaniu średniej nie uwzględniam wyników które najbardziej odbiegaj od innych; są to pomiary nr 1-3.

2. KRÓTKA TEORIA TEMATU OGÓLNEGO

Falą nazywamy zaburzenie mechaniczne lub elektromagnetyczne rozchodzące się w czasie
i przestrzeni z określoną prędkością, charakterystyczną dla danego rodzaju fal i ośrodka,
w którym fale się rozchodzą.

Jeżeli wybraną cząstkę jednowymiarowego ciągłego ośrodka materialnego pobudzimy
w dowolny sposób do drgań harmonicznych, to jej drgania można opisać równaniem:

y = Asin( ω t ) , gdzie y jest wielkością wychylenia cząstki z położenia równowagi,

A - amplituda drgań ( największym wychyleniem ), ω - częstością kołową,

t - czasem, natomiast ωt fazą drgań. Drgania te będą się przenosić na cząstki sąsiednie. Wielkość opóźnienia będzie proporcjonalna do odległości x tych cząstek od cząstki pierwotnej ( źródła fali ). Równanie ruchu dla tych cząstek przyjmuje więc następującą postać:
y = Asin( ωt - kx ). Odległość pomiędzy punktami ośrodka, dla których różnica faz wynosi 2Π stanowi długość fali i oznaczamy ją symbolem - λ . Jeżeli więc ( ωt - kx1 ) - ( ωt - kx₂ ) = 2Π, to x₂ - x₁ = λ.

Podstawiając tak określoną wielkość k do równania y = Asin( ωt - kx ) oraz przyjmując, że
ω = 2Π / T

( T - okres drgań ) otrzymamy: y = A sin 2Π . Jest to równanie dla przypadku jednowymiarowego.

Niektóre zjawiska związane z ruchem falowym można wyjaśnić w oparciu o zasadę Huygensa, według której każdy punkt, do którego dociera czoło fali, można traktować jako źródło fali kulistej, tzw. elementarnej fali cząstkowej.

Rozpatrzmy przypadek, gdy fala płaska przechodzi z jednego ośrodka do drugiego, przy założeniu, że prędkości fali

w obu ośrodkach są różne i wynoszą: w ośrodku I - v1, a w ośrodku II - v₂ ( v₁ > v₂ ); odpowiadające im długości fali są λ₁ i λ₂.

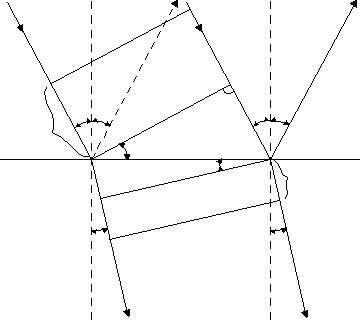
Rys 1. Przejście fali płaskiej przez granicę dwóch ośrodków o różnych prędkościach rozchodzenia

się fali.

Przyjmując, że kierunki SA i SC rozchodzenia się fali padającej tworzą kąt α z prostą prostopadłą do powierzchni rozgraniczającej ośrodki. Na granicy ośrodków fala zostanie częściowo odbita w kierunku prostych AS1 i CS1, częściowo przejdzie do drugiego ośrodka i będzie rozchodzić się w kierunkach AS2 i CS2.

W czasie Δt, w przeciągu którego fala w ośrodku I rozejdzie się na odległość BC = v₁ *Δt,
w ośrodku II z punktu A rozejdzie się na odległość AD = v₂ * Δt. Z punktów pośrednich, leżących pomiędzy A i C, też rozejdą się fale cząstkowe - oczywiście na odległość odpowiednio mniejsze. Czoło fali rozchodzącej się w ośrodku II, stanowi obwiednię fal elementarnych, będzie płaszczyzną. To oznacza, że po przejściu granicy dwu ośrodków fala płaska pozostaje falą płaską.

W związku z założeniem, że v₁ ≠ v₂ promien fali rozchodzącej się w ośrodku II, będzie tworzył z normalną do powierzchni rozgraniczającej β ≠ α. Kąt β nazywamy kątem załamania fali.
Z konstrukcji geometrycznej przedstawionej na rysunku wynika, że

AC * sinα = BC = v₁ * Δt = λ₂

oraz AC * sinβ = AD = v₂ * Δt = λ₂

Dzieląc stronami równanie pierwsze przez drugie otrzymamy
₂₁
. A więc stosunek sinusa kąta padania do sinusa kąta załamania fali, dla danych dwu ośrodków, jest wielkością stałą i równą stosunkowi prędkości fali w tych ośrodkach. Wielkość tę oznaczamy przez n21 i nosi ona nazwę współczynnika załamania ośrodka drugiego względem pierwszego. W oparciu o zasadę Huygensa można wykazać, że α = α`, oraz że promień padający , promień odbity i normalna w punkcie padania leżą w jednej płaszczyźnie. Formuła ta stanowi prawo odbicia fali.

2a. KRÓTKA TEORIA ĆWICZENIA OP.1.1

Posługując się pojęciem promieniowania świetlnego rozpatrzmy prawo odbicia i załamania światła (tzw. Prawo Snelliusa). Rys 2 ilustruje zjawisko odbicia i załamania promienia świetlnego na granicy ośrodków I i II gdzie:

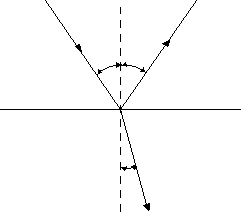
SO - promień odbity

OP- promień załamany

O - punkt padania

NN₁ - normalna padania

Kąt SON - kąt padania

Kąt NOS₁ - kąt odbicia

Kąt NOP - kąt załamania

Prawo odbicia i załamania brzmi następująco:

Rys 2. Odbicie i załamanie promienia świetlnego.

1. promień padający, odbity i załamany oraz normalna padania leżą w tej jednej płaszczyźnie.

2. Kąt odbicia jest równy kątowi padania,

3. Stosunek kąta padania i kąta załamania promienia świetlnego jest wielkością stałą dla danych dwóch ośrodków i określonej długości fali; nazywamy go współczynnikiem załamania ośrodka II względem I.

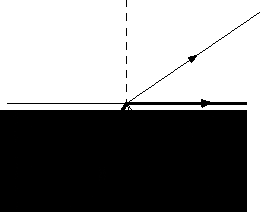
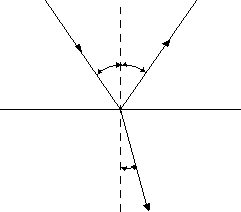
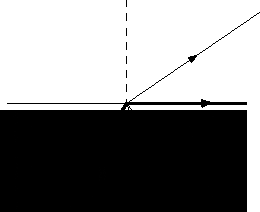
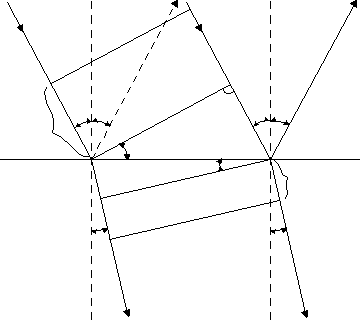
Jeżeli promień świetlny biegnie z ośrodka optycznie gęstszego do ośrodka optycznie rzadszego, to na granicy tych ulega on załamaniu, odchylając się od normalnej padania. Przy pewnym kącie α=γ promień załamany biegnie wzdłuż powierzchni granicznej. Kąt γ nazywamy kątem granicznym.

3. OPIS WYKONANIA ĆWICZENIA

W celu wyznaczenia współczynnika załamania, umieszczamy próbkę nr 1 na tarczy z podziałką kątową. Na jej płaską ścianę rzucamy w punkcie centralnym wąski strumień światła i mierzymy kąt padania oraz kąt załamania. Pomiary wykonujemy dla dziesięciu różnych kątów α. Następnie oświetlając próbkę od strony wypukłej, znajdujemy jej kąt graniczny.

4. RACHUNEK BŁĘDÓW

Błąd względny maksymalny możliwy do popełnienia (Δα i Δβ wyrażamy w mierze łukowej):

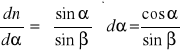
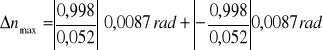
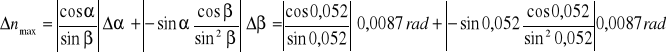
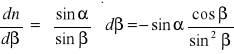
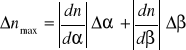
2

S₂

S₂

A

C

α α`

λ₁

λ₂

α α`

β

β

D

β

α

Rys 3 Przejście promienia z ośrodka optycznie gęstszego do rzadszego.

I

II

β

d

S

N

S₁

O

I

II

N₁

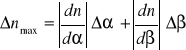
n₂

P

n₁

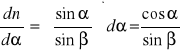
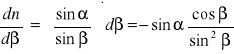
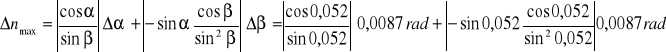
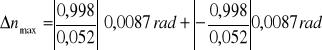
n₁ 1

β

N

D

I β

2

n₂>n₁

II α α`

n₂

3 γ 3

2

1 N₁ 1

II

I

S₂

S₂

B

S₁

λ₂

α α`

α α`

λ₁

α

β

β

A

C

S

S

S

---