1.1 Praktyczne przykłady (odpowiedniki) strzałkowania.
Napięcie i jednocześnie prąd w dwójniku (elemencie posiadającym dwa zaciski) można zastrzałkować odbiornikowo (napięcie przeciwnie do prądu) rys. 1.1 a, albo źródłowo (napięcie i prąd zgodnie) rys. 1.2 b.
Rys. 1.1 Dwójnik zastrzałkowany odbiornikowo
Odbiornikowemu zastrzałkowaniu w praktyce może odpowiadać włączenie amperomierza i woltomierza jak na rysunku 1.1 b. Gdyby zamienić zaciski amperomierza to taki układ odpowiadałby zastrzałkowaniu odbiornika jak na rysunku 1.2 a (zastrzałkowanie źródłowe).
Rys.1.2 Dwójnik zastrzałkowany źródłowo
Inną interpretacją zastrzałkowania w praktyce może być obserwacja napięcia i prądu na elemencie przy pomocy oscyloskopu. Na rysunku 1.2b podano sposób pomiaru odpowiadający zastrzałkowaniu źródłowemu.
Rys.1.3 Przykładowe przebiegi uzyskane z pomiaru napięcia i prądu oscyloskopem dla układu z rys. 1.2
Zastrzałkowanie dwójnika odbiornikowe bądź źródłowe nie określa jeszcze charakteru jego pracy. Na rysunku 1.3 przedstawiono możliwe przebiegi napięcia i prądu przy czym z rysunku 1.3a wynika, że dwójnik zastrzałkowany odbiornikowo (rys. 1.2) pobiera energię, natomiast w przypadku przebiegów otrzymanych jak na rys. 1.3b wydaje energię.
UI>0 źródło UI>0 odbiornik
UI<0 odbiornik UI<0 źródło
Rys. 1.4 Interpretacja znaku mocy i zastrzałkowania dwójnika.
Iloczyn napięcia i prądu określa moc elektryczną pobieraną (lub oddawaną przez dwójnik 1.1). W obwodach prądu stałego jednostką mocy jest wat (W).
![]()
albo tak ![]()
(1.1)
Podsumowując: jeżeli dwójnik jest zastrzałkowany źródłowo to iloczyn napięcia i prądów otrzymanych dla takiego zastrzałkowania (czy to z pomiarów, czy z obliczeń) będziemy nazywać mocą wydawaną, natomiast dla napięcia i prądu uzyskanych dla zastrzałkowania odbiornikowego ich iloczyn określa moc pobieraną. Oczywiście dopiero znak tej mocy decyduje czy odbiornik pracuje w charakterze źródła czy odbiornika.
1.2 Modele elementów rzeczywistych.
Rezystorem nazywamy urządzenie , którego główną cechą jest wielkość elektryczna zwana rezystancją R . Rezystorem idealnym będziemy nazywali urządzenie , które można zamodelować za pomocą tylko rezystancji. Inaczej rezystor idealny to dwójnik w , którym energia elektryczna zamienia się na tylko ciepło (dyssypatywność) stąd rezystancje nazywamy dwójnikiem pasywnym . Rezystancja dwójnika (idealnego) to wielkość proporcjonalna do przyłożonego napięcia , a odwrotnie proporcjonalna do płynącego prądu. Jednostką rezystancji jest ohm mający wymiar wolta przez amper. Zależność powyższa określana jest mianem Prawa Ohma ( 1.2).
(1.2)
Rys.1.5 Schemat elektryczny rezystancji zastrzałkowany odbiornikowo
Dla rezystora zastrzałkowanego odbiornikowo zawsze ![]()
gdyż ![]()
lub ![]()
W dalszym ciągu dwójnik , o którym wiadomo , że jest rezystancją będziemy strzałkować zawsze odbiornikowo . Jeżeli charakterystyka napięciowo-prądowa dwójnika jest dana funkcją liniową (1.3) to mówimy wówczas , że dwójnik jest liniowy (rys. 1.6)
![]()
(1.3)
Rys.1.6 Charakterystyka rezystancji liniowej
Wielkość fizyczna będąca odwrotnością rezystancji , nazywa się przewodnością albo konduktancją . Jednostką konduktacji jest simens
G - konduktancja ![]()
(1.4)
Elementy obwodu są połączone przewodami, których rezystancja jest z reguły dużo mniejsza od rezystancji elementów obwodu . Wówczas przewody modelujemy jako elementy bezrezystancyjne (rys. 1.7), to jest takie, na których nie ma spadku napięcia.
![]()
Rys.1.7 Przewód idealny (bezrezystancyjny)
Jeżeli pominięcie rezystancji spowodowałoby zbyt duże błędy to należy przewód zamodelować jako rezystancje, która dla przewodu o stałym przekroju określa wzór:
![]()
(1.50)
gdzie: ![]()
- odpowiednio rezystywność i konduktywność materiału z którego zrobiono przewodnik
Wówczas przewód rzeczywisty modelujemy jak rezystancję (rys1.8).
Rys.1.8 Przewód rzeczywisty
Jeżeli ![]()
to rezystor nazywamy nieliniowym a jego charakterystyka nie jest linią prostą i może mieć postać jak na rys. (1.9). Stosunek napięcia do prądu w danym punkcie pracy nazywamy wówczas rezystancją statyczną. Jeżeli obwód zawiera chociaż jeden element nieliniowy to mówimy, że obwód jest nieliniowy. Metody rozwiązania takich obwodów przedstawiono w rozdziale 3.
Rys.1.9 Charakterystyka napęciowo-prądowa elementu nieliniowego
1.3 Źródła idealne (niezależne, autonomiczne)
Źródłami napięcia lub prądu elektrycznego nazywa się przetworniki innych rodzajów energii w energię elektryczną. Inaczej źródło to element aktywny w trwały sposób utrzymujący napięcie między zaciskami zewnętrznymi (źródło napięciowe) lub prąd w gałęzi (źródło prądowe).
Schematy źródeł
a) b)
c) d)
Rys.1.10 Schemat źródeł idealnych napięciowych i prądowych: a,c- schematy najczęściej występujące w literaturze b,d- schematy obowiązujące według polskiej normy PN.
Rys.1.11 Punkt przecięcia się charakterystyk idealnych z charakterystyką obciążenia
SEM i SPM źródeł autonomicznych (wymuszeń) nie zależą odpowiednio od prądu, lub napięcia (odpowiedzi). Źródła, które można zamodelować za pomocą tylko SEM i SPM nazywa się idealnymi . W rzeczywistości takie źródła nie istnieją i można je tak modelować tylko w określonych warunkach pracy. Modele źródeł rzeczywistych przedstawiono w rozdziale (3.5).
1.4 Źródła sterowane.
Wśród istotnych elementów występujących zwłaszcza w obwodach elektronicznych , należy wymienić źródła sterowane . Zasada działania takiego źródła polega na tym , że jego SEM albo SPM zależy do sygnału sterującego , czyli napięcia albo prądu występującego w innym fragmencie obwodu . Symbole graficzne określające różne typy źródeł przedstawiono na rys. (1.12)
![]()
Rys.1.12 Symbole graficzne żródeł sterowanych .
Źródła sterowane mają (charakter), strukturę czwórników.
1.5 Podstawowe właściwości topologiczne obwodu.
Gałąź- odcinek obwodu, w którym prąd w dowolnej chwili ma tę samą wartość.
Na rys. 1.13 przedstawiono graf obwodu , a więc schemat uwzględniający tylko gałęzie.
Rys.1.13 Graf obwodu złożony z sześciu gałęzi
Węzeł obwodu - punkt, w którym łączą się co najmniej trzy gałęzie.
Obwód zamknięty - połączenie gałęzi tworzące kontur (drogę) zamkniętą.
Oczko obwodu - połączenie gałęzi tworzące kontur zamknięty, w środku którego nie ma
żadnej gałęzi.
Na rys. 1.14 przedstawiono graf obwodu, w którym można wyróżnić 4 węzły 3 oczka oraz 5 dróg tworzących obwód zamknięty.
Rys.1.14 Graf obwodu zawierający 4 węzły i składający się z 3 oczek
Obwód nieplanarny - gdy gałęzie skrzyżowane nie tworzą węzła (brak połączenia galwanicznego)
Rys 1.15 Przykład obwodu nieplanarnego
Liczba oczek obwodu
Można wykazać ,że obwód składający się z g - gałęzi i w- węzłów składa się z liczby oczek danej wzorem :
Gdzie : g- liczba gałęzi
w- liczba węzłów o = g-w+1 (1.5)
o- liczba oczek
Rys.1.16 Grafy planarne obwodów
1.6 Prawa Kirchhoffa
Prąd jest wielkością skalarną definiowaną najczęściej jako zmiana w czasie, płynącego ładunku q przy czym prąd chwilowy określa wzór (1.7):
![]()
(1.7)
Z drugiej strony z prądem związana jest wielkość wektorowa zwana gęstością prądu, której moduł określany jest przez (1.8):
![]()
(1.8)
Jeżeli zatem gęstość prądu w przekroju poprzecznym przewodnika nie jest stała (np. przy przepływie prądu zmiennego) to prąd może być wyrażony jako strumień wektora gęstości prądu (1.9):
![]()
(1.9)
W obwodzie ,w którym występuje przepływ prądu obowiązuje zasada: strumień gęstości prądu przez zamkniętą powierzchnię jest równy 0 albo inaczej: w tym samym czasie ładunek wpływający do danej objętości jest równy ładunkowi wypływającemu z niej. Zasada ta nazywana jest I prawem Kirchhoffa w postaci całkowej (1.10):
I Prawo Kirchhoffa
Postać całkowa:
![]()
(1.10)
Rys.1.17 Fragment obwodu z prądem z zaznaczoną powierzchnią zamkniętą
Całkowity strumień przez powierzchnią zamkniętą (rys.1.17) przy założeniu stałej gęstości w danym przekroju przewodnika określa się następująco:
![]()
α1=< (J1, dS) = 180 cos 180 = -1 znaki prądu wynikają z faktu , że pod całką ၡ2= < (J2, dS) = 0 cos α2 = 1 występuje iloczyn skalarny gęstości prądu ၡ3= < (J3, dS) = 0 cos α3 = 1 i wektora orientacji powierzchni dS
Ostatecznie I Prawo Kirchhoffa (dalej w skrócie IPK) w postaci algebraicznej ma postać:
Σik = 0 (1.14)
Prawo to można wyrazić następująco : algebraiczna suma prądów wpływających do węzła (prąd wpływający np. z plusem a wypływający z minusem ) jest równa zero.
Wykorzystując I prawo Kirchhoffa można wykazać, iż nie da się przesłać energii elektrycznej miedzy dwoma układami jednym przewodem (czasami jako tor powrotny wykorzystuje się ziemię), gdyż prąd w tym przewodzie zgodnie z IPK musi być równy zero (rys 1.18).
Rys.1.18 Przypadek dwóch obwodów połączonych jednym przewodem.
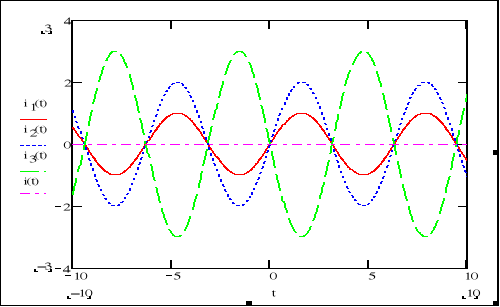
Prawo Kirchhofa musi być spełnione w każdej chwili czasowej bez względu na to czy prądy płynące w gałęziach są stałe czy zmienne. Na rys 1.19 przedstawiono wyniki symulacji prądów „wpływajacych” do węzła pewnego obwodu. Suma wartości chwilowych tych prądów w każdej chwili jest równa zero.
i1(t)+ i2(t)+ i3(t)=i(t)=0
Rys. 1.19 Pierwsze Prawo Kirchhoffa jest spełnione w każdej chwili czasowej
Liczba węzłów niezależnych
Jeżeli obwód ma „w” węzłów to można napisać „w”- równań.
Twierdzenie: Obwód zawierający „w” węzłów ma „w-1” węzłów niezależnych.
II Prawo Kirchhoffa (IIPK)
W przewodzie, w którym płynie prąd, ładunki elektryczne poruszają się pod wpływem pola elektrycznego. Ze względu na to, że do każdej objętości tyle samo ładunków dopływa, jak i odpływa, pole elektryczne na zewnątrz przewodnika jest takie samo jak pole elektrostatyczne wywołane przez nieruchome ładunki. Stąd znajdują zastosowanie takie wielkości jak natężenie pola elektrycznego E czy potencjał V w punkcie tego pola. W teorii pola napięcie między dwoma punktami w obszarze w którym występuje pole E wyraża się zależnością:
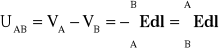
(1.15)
gdzie: VA,VB - potencjał elektryczny pola odpowiednio w punkcie A i B
W praktyce w teorii obwodów jako potencjał odniesienia można przyjąć dowolny punkt obwodu i przyjąć dowolną wartość (patrz paragraf 3.3). Ze względu na to, że pole elektrostatyczne jest bezwirowe, stąd całka krzywoliniowa po drodze zamkniętej jest równa zero, a to oznacza, że suma napięć określonych na tej drodze jest też równa zero:
![]()
![]()
(1.16)
gdzie: znak Uk zależy od orientacji oczka.
Prawo określone wzorem (1.16) jest II Prawem Kirchhoffa (dalej IIPK) odpowiednio w postaci całkowej lub algebraicznej. W teorii obwodów zastosowanie znajduje przede wszystkim IIPK w postaci algebraicznej które można wyrazić następująco:
Algebraiczna suma napięć (np. z plusem jeżeli napięcie jest zgodne z przyjętym obiegiem dla danej drogi, a z minusem jeżeli przeciwne) wzdłuż dowolnej drogi zamkniętej jest równa zero.
Przykład 1.1
Wyróżnijmy w obwodzie pewną drogę zamkniętą
Sformułowane równanie na podstawie II prawa Kirchhoffa dla drogi ABCDEFGA:
-E1-I1R1+E2-I3R2-I4R3-I5R4+UI-IR5=0
Dla g - gałęzi oraz „w” węzłów istnieje: o=g-w+1 niezależnych równań napięciowych z II Prawa Kirchhoffa.
Wniosek:
w-1 niezależnych równań z I Prawa Kirchhoffa
g-w+1 niezależnych równań z II Prawa Kirchhoffa
![]()
równań = liczbie niewiadomych prądów w gałęziach
W przypadku SPM liczba niewiadomych prądów zamienia się na niewiadome UI źródeł SPM.
g=6, w=4, o=6-4+1=3
IE+I1-I=0
I+I3-I2=0
-IE-I1+I4=0
-I4+I2-I3=0
![]()
0 = 0
I=IE+I1
I4=IE+I1
UKŁAD RÓWNAŃ z I i II prawa Kirchhoffa.
E+I1R1=0
UI-I2R2-I4R4-I1R1=0
E3-I2R2-I3R3=0
IE+I1-I=0
I+I3-I2=0
I=I4
1.7 Równoważne dwójniki pasywne
Rys.1.23 Dwa równoważne dwójniki
Definicja:
Dwa dwójniki uważamy za równoważne jeżeli przy jednakowym wymuszeniu powstaje jednakowa odpowiedź.
Czyli dwójniki z rys. 1.23 będą równoważne jeżeli przy jednakowym napięciu zasilania U popłynie przez dwójniki jednakowy prąd I.
Rodzaje połączeń dwójników:
Połączenie szeregowe - jednakowy prąd.
Połączenie równoległe - jednakowe napięcie.
Rys.1.24 Równoważna (zastępcza) rezystancja szeregowo połączonych rezystorów.
Z II Prawa Kirchhoffa otrzymamy:
U-U1-U2-U3=0
U=I(R1+R2+R3) U=IRZ
Zatem dwójniki na rys.1.24 będą równoważne jeżeli :
R1+R2+R3=RZ
Ogólnie wzór na połączenie szeregowe rezystancji ma postać:
RZ=RK
Równoważna (zastępcza) rezystancja równolegle połączonych rezystorów
Z IPK mamy:
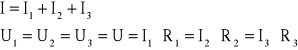
![]()
![]()
![]()
Wstawiając powyższe prądy do I-go prawa Kirchhoffa otrzymamy:

stąd 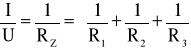
Ogólnie wzór na połączenie równoległe ma postać:
![]()
lub ![]()
Warto zauważyć że jeżeli R1=R2=R3=...RN=R to ![]()
Przykłady do rozdziału 1.1
Zad. 1.1
Oblicz wskazania mierników oraz moc wydzielaną przez źródło (mierniki idealne).
Dane
E = 100 [V]
Rk+1 = Rk + 2 [Ω]
gdzie k= 1...5
oraz R1 = 2 Ω
Na podstawie wzoru na rezystancje wiedząc że R1 = 2 Ω następne rezystancje mają wartości:
R2 =4 Ω; R3 =6 Ω; R4 =8 Ω; R5 =10 Ω; R6 =12 Ω.
Obwód po zastosowaniu i założeniu , że mierniki są idealne ma postać:
![]()
Obwód po połączeniu równoległym:
Jak można zauważyć I3 = I4 = (I5 + I6)
R3456 = R3 + R4 + R56 = 6 + 8 + 5.455 = 19.455 Ω
Po połączeniu równoległym R2 i R3456:
![]()
Łącząc szeregowo R1 i R23456 otrzymany:
Rz= R1+ R23456 = 2 + 3.318 = 5.318 Ω
Korzystając z prawa Ohma można wyliczyć I1
![]()
Moc wydzielana przez źródło :
P = E · I1 = 100 · 18.805 = 1880.5 W
Wskazanie woltomierza to:
U23456 = I1 · R23456 = 18.805 · 3.318 = 62.395 V
Wskazanie amperomierza to wartość prądu I3:
![]()
Odpowiedź:
Wskazanie amperomierza wynosi 3.207A
Wskazanie woltomierza wynosi 62.391 V
Moc wydzielana przez źródło 1880.5 W
Zad. 1.2
Rozwiązać obwód metodą praw Kirchhoffa . Oblicz wskazania mierników
Dane:
E = 20 V + 2n [V]
Rk+1 = Rk + 2 [Ω]
gdzie k= 1..6
oraz R1 = 0 Ω
dla n = 15
E = 50 V
Poszczególne rezystancje
wynoszą:
R1= 0 Ω; R2= 2 Ω; R3= 4 Ω
R4= 6 Ω; R5= 8 Ω; R6= 10 Ω
R7= 12 Ω.
m - liczba gałęzi
α - liczba węzłów
w celu otrzymania rozwiązania obwodu układam w - 1 równań na podstawie I P.K., a pozostałe g - w + 1=o równań układam na podstawie II P.K. dla wszystkich niezależnych oczek obwodu.
W tym przykładzie o = 3; w = 4
I P.K. w - 1 = 3
Układamy równania dla węzłów oznaczonych a, c, d
a → I1 = I3 + I4
c → I1 = I5 + I7
d → I4 = I6 + I7
Liczba równań z IIPK wynosi: m - α + 1 = 3
Układamy równania dla oczek oznaczonych A, B, C
A → - R4I4 - R6I6 + R3I3 = 0
B → R6I6 - R7I7 + R5I5 = 0
C → - R1I1 - R3I3 - R5I5 - R2I1 + E = 0
Po podstawieniu wartości rezystancji oraz wartość napięcia źródła
- 6I4 - 10I6 + 4I3 = 0
10I6 - 12I7 + 8I5 = 0
- 4I3 - 8I5 - 2I1 + 50 = 0
z równań dla I P.K. podstawiam prądy (I3, I5, I6) tak aby uzyskać układ trzech równań z trzema niewiadomymi:
- 6I4 - 10(I4-I7) + 4(I1-I4) = 0
10(I4-I7) - 12I7 + 8(I1-I7) = 0
- 4(I1-I4) - 8(I1-I7) - 2I1 = - 50
- 6I4 - 10I4 + 10I7 + 4I1- 4I4 = 0
10I4 - 10I7 - 12I7 + 8I1- 8I7 = 0
- 4I1+ 4I4 - 8I1+ 8I7 - 2I1 = - 50
4I1
- 20I4 + 10I7 = 0
8I1+ 10I4 - 30I7 = 0
- 14I1 + 4I4 + 8I7 = - 50
Powyższy układ równań można napisać w postaci macierzowej:
![]()
![]()
gdzie:

Zatem:
![]()
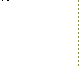
I3 = I1 - I4
I5 = I1 - I7
I6 = I4 - I7
Aby obliczyć wartość wskazywaną przez woltomierz trzeba obliczyć wartość prądu gałęziowego I6
I6 = 2.174 - 2.174
I6 = 0
Jak wynika z obliczeń w gałęzi 6 prąd nie płynie i dlatego na rezystancji R6 nie odkłada się żadne napięcie. Fakt zerowej wartości prądu I6 można stwierdzić automatycznie z warunku równowagi mostka (patrz przykład x).
Odpowiedź:
Amperomierz wskazuje 5,43 [A],
Woltomierz wskazuje 0[V].
Zad.1.3
Określ wartość rezystancji R w układzie zwanym układem poprawnie mierzonego napięcia (rys.P1.3) jeżeli wskazanie amperomierza IA = 1A, a woltomierza UV = 10V, oraz jeżeli mierniki są rzeczywiste o wartościach rezystancji: RA = 10mΩ oraz RV = 2kΩ.
Oblicz wartość rezystancji pomiarowej określonej jako stosunek![]()
(przy znajomości RA i RV jak wyżej ) jeżeli rzeczywista rezystancja wyniosłaby:
R =10Ω
R =5kΩ
Wylicz procentowy błąd popełniany przy określaniu rezystancji pomiarowej.
Ad 1.
Aby obliczyć wartość rezystancji R należy skorzystać z prawa Ohma oraz Kirchhoffa
Dane:
IA = 1A UV = 10V RA = 10m Ω RV = 2kΩ
R =?
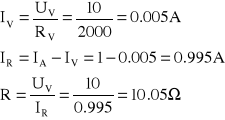
Ad. 2a
Dane:
Wartość rzeczywista rezystancji R = 10Ω;
RA = 10mΩ RV = 2kΩ

rezystancja pomierzona wynosi Rp:
![]()
stąd: ![]()
Wstawiając w miejsce Rp wyrażenie określające RRV otrzymujemy wzór z którego wynika, że błąd pomiarowy w tym układzie zależy tylko od wartości mierzonej rezystancji i rezystancji woltomierza:
![]()
Ad. 2b
Rezystancja rzeczywista R = 5kΩ
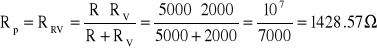
Względny błąd procentowy wynosi:
![]()
Odpowiedź:
Ad.1 Obliczona wartość rezystancji wynosi 10.05Ω.
Ad. 2a Dla pomiaru rezystancji o wartości 10Ω w układzie poprawnie mierzonego napięcia błąd względny procentowy wynosi -0.498%.
Ad. 2b Dla pomiaru rezystancji o wartości 5000Ω tą metodą błąd względny procentowy wyniósł -71.42%.
Układ poprawnie mierzonego napięcia daje dokładniejsze wyniki dla rezystancji zdecydowanie mniejszych od rezystancji woltomierza, błąd dla tej metody jest zawsze ujemny.
Zad.1.4
Określ wartość rezystancji R jeżeli wskazanie amperomierza IA = 1A, a woltomierza UV = 10V, oraz jeżeli mierniki są rzeczywiste o wartościach RA = 10mΩ oraz RV = 2kΩ.
Wylicz procentowy błąd popełniany przy określaniu rezystancji jako stosunek ![]()
jeżeli rzeczywista rezystancja wyniosłaby:
R =50 mΩ
R =500Ω
Ad 3.
Dane:
IA = 1A
UV = 10V
RA = 10mΩ
RV = 2kΩ
R =?
Z II prawa Kirchhoffa
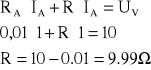
Ad. 4a
R =50 mΩ; RA = 10m Ω RV = 2kΩ
![]()
Względny błąd procentowy wynosi:
![]()
Ad. 4b
R =100Ω
Rp=RA+R=100.01
![]()
odpowiedzi:
Ad.3
obliczona wartość rezystancji wynosi 9.99Ω.
Ad. 4a
dla pomiaru rezystancji o wartości 50mΩ w układzie poprawnie mierzonego prądu błąd względny procentowy wynosi 20%.
Ad. 4b
dla pomiaru rezystancji o wartości 100Ω tą metodą błąd względny procentowy wynosi 0.01%.
Układ poprawnie mierzonego prądu daje dokładniejsze wyniki dla rezystancji zdecydowanie większych od rezystancji amperomierza.
Zad.1.5
Oblicz wskazania mierników oraz moc żarówek przy zasilaniu napięcieciem nominalnym. Zbadaj jaką moc pobierają żarówki przy połączeniu szeregowym :
Dane znamionowe pojedynczej żarówki :
UN = 110V
PN = 100W
Dane dotyczące parametrów obwodu: E = 110V RW = 2Ω
Rozwiązanie:
Obliczamy moc dwóch żarówek: ![]()
Obliczamy rezystancję żarówek z zależności: 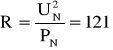
Zatem rezystancja zastępcza obu żarówek wynosi: ![]()
Prąd w obwodzie (wskazanie amperomierza): ![]()
Wskazanie woltomierza: ![]()
Wskazanie watomierza: ![]()
W przypadku połączenia szeregowego ![]()
Stąd moc pobierana przez obie żarówki: 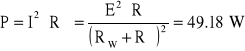
Czy można zatem powiedzieć że dwie takie same rezystancje będą pobierały większą moc w przypadku połączenia równoległego, aniżeli w przypadku połączenia szeregowego.
Żeby odpowiedzieć na to pytanie określmy funkcje mocy dla obu przypadków:
Jeżeli połączymy dwie rezystancje R szeregowo do rzeczywistego źródła to funkcja mocy ma postać: 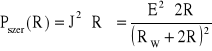
Natomiast w przypadku połączenia tych rezystancji funkcja mocy ma postać:
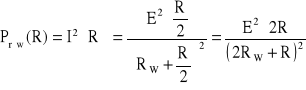
Z powyższego rysunku wynika, że dla rezystancji obciążenia R mniejszej od Rw
(dla danych z zadania Rw=2) większą moc będzie pobierał układ szeregowo połączonych takich rezystancji, natomiast dla R> Rw układ rezystancji połączonych równolegle.
Odpowiedzi:
Wskazanie woltomierza: U = 106.5V
Wskazanie watomierza: P = 187.2W
Moc przy połączeniu szeregowym P=49.18 W
Zad.1.6
Do zacisków a-b dwójnika źródłowego (zastępczego rzeczywistego żródła napięcia) przyłączono idealne źródło o napięciu E = 120V i zmierzono prąd I = 10A, a po zmniejszeniu E o 10V prąd zwiększył się do 30A. Wyznaczyć napięcie ![]()
w stanie jałowym i przy obciążeniu prądem 45A.
Dwójnik źródłowy można przedstawić w postaci źródła napięciowego i rezystancji, połączonych szeregowo i wówczas szukane napięcie w stanie jałowym Uab = Eź (rys.P1.6).
rys.P1.6
Z IIPK układamy równanie przy zastrzałkowaniu źródłowym Eź:
![]()
Po podstawieniu za E wartości 120V i za I wartości 10A, mamy dwie niewiadome w równaniu:
![]()
Drugie równanie otrzymamy z układu z obniżonym napięciem E = 110V (rys.P1.6.1) przy czym zakładamy, że prąd nie zmienił zwrotu.
![]()
rys.P1.6.1
![]()
Po rozwiązaniu układu:
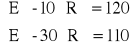
![]()
otrzymujemy:
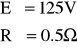
Należy zwrócić uwagę, że w treści zadania nie jest podany kierunek prądu, ani przed, ani po zmniejszeniu napięcia E. Zatem należałoby sprawdzić jeszcze dwa przypadki:
b) prąd po zmniejszeniu E zmienia zwrot,
c) prąd przed zmniejszeniem E ma zwrot w „lewo” , a po zmniejszeniu w prawo.
W przypadku b) otrzymamy równania:
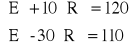
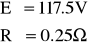
W przypadku c) wynik rezystancji jest ujemny
Gdyby założyć przeciwny zwrot źródła Eź to po rozwiązaniu odpowiednich układów równań wartość tego SEM wyszłaby i tak ujemna (czyli zwrot jak dotychczasowy) co jest zrozumiałe gdyż w oczku dwie siły SEM jednakowo zwrócone mogą wymusić prąd w jednym kierunku, a zmniejszenie jednej z nich nie mogłoby spowodować wzrostu tego prądu.
Wyznaczamy napięcie dwójnika w stanie jałowym (![]()
, nie ma spadku napięcia na rezystancji)( rys.P1.6.2)
![]()
rys.P1.6.2
![]()
lub 117.5V
Wyznaczamy napięcie dwójnika w stanie gdy prąd ![]()
( rys.P1.6.3)
rys.P1.6.3
![]()
dla przypadku a) ![]()
dla przypadku b) ![]()
Odp: Napięcie Uab w stanie jałowym(![]()
A) wynosi 125V lub 117.5V, a przy obciążeniu prądem ![]()
wynosi odpowiednio 102.5V lub 106.25V.
Zarys teorii obwodów w zadaniach (proste obwody prądu stałego)
_________________________________________________________________________________________________________________
1
24
I
U
R
![]()
I[A]
U[V]
![]()
![]()
![]()
![]()
40
30
20
10
1 2 3 4
U=0
![]()
![]()
![]()
R
I
R
Iz
E
R
I
U
Idealne źródło napięciowe SEM-siła elektromotoryczna
U
Idealne źródło prądowe SPM -siła prądomotoryczna
U
I
R
I
U
![]()
punkt
pracy
U
E
![]()
I
I
I
Iz
U
punkt
pracy
![]()
![]()
źródło napięciowe sterowane
napięciem ŹNSN
źródło napięciowe sterowane
prądem ŹNSP
![]()
![]()
źródło prądowe sterowane
prądem ŹPSP
![]()
![]()
![]()
źródło prądowe sterowane
napięciem ŹPSN
![]()
A
C
B
D
![]()
![]()
![]()
![]()
![]()
![]()
![]()
D
B
C
A
5
4
3
2
1
![]()
![]()
![]()
![]()
1
2
3
4
5
6
7
8
o=8-5+1=4
1
2
3
4
5
6
o=6-4+1=3
I4
I5
I6
U
I
V
A
Rb
U=IRb![]()
I
U
U,I
U>0
I<0
t
U,I
U>0
I>0
t
I
U
I
U
dS
S3
S2
S1
J1
dS
dS
J2
J3
sieć
sieć
i=0
i1
i1
i2
i3
i3
1
2
i1-i2-i3=0
-i1+i2+i3=0
0=0 równania zależne
i1
i2
i3
A
B
C
D
E
F
G
I
I
R1
R2
R3
R4
E1
E2
UI
I1
I2
I3
I4
I5
R5
a)
E
E3
R1
R2
R3
I1
I4
I3
I3
IE
I
I2
1
2
3
4
Jedno równanie jest zależne
sieć
sieć
I4
I
- ![]()
I4=I
B
I i1(t
A
I
U
U
I
U
RZ
UZ
I
R1
R2
R3
U1
U2
U3
U
U
I
U1
I1
R1
U2
I2
R2
U3
I3
R3
U
I
V
*
W
*
A
A
2 →
2
1
RV
RA
I
IV
IA
UV
R
E
V
A
RV
RA
IA
IV
IR
UV
R
E
V
A
z I P.K. można łatwo obliczyć pozostałe prądy
I1
I4
I7
Rys.P1.3

= 0
R4
R1
R6
R7
R5
R3
R2
I7
I5
I6
I4
I3
I1
d
A
B
CA
a
c
b
V
A
E
I1
Rz
E
R23456
E
R1
I1
R3456
E
R2
R1
I1
I2
I3
I3
I2
I1
R1
R3
R56
R2
E
R4
I6
I5
I3
I2
I1
I4
R1
R3
R6
R5
R4
R2
E
R2
V
R4
R6
R5
A
R3
R1
E
RŻ
UN
E
RW
I
Dwójnik
źródłowy
A
a
b
.
.
Eź
Rź
a
b
E = 120V
.
.
A
Eź
Rź
a
b
E = 110V
.
.
Eź
Rź
a
b
I = 0
.
.
Eź
Rź
R
I = 45A
a
b
![]()
![]()
b)
a)
b)
RZ