POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI |
||
Paweł Proń |
Sprawozdanie z ćwiczenia nr 9 Temat: Pomiar przewodności cieplnej izolatorów |
|
Wydział Elektroniki Rok I |
Data: 30.04.1998 |
Ocena: |
I.Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie ćwiczących z zagadnieniami przenoszenia ciepła, z podstawowymi jego mechanizmami, a także z metodą pomiaru przewodności cieplnej izolatorów i pomiarze współczynnika przewodności cieplnej izolatora.
II. Wstęp teoretyczny.
Jeżeli pomiędzy różnymi ciałami (które są połączone) lub elementami tego samego ciała powstanie różnica temperatur, to następuje samorzutny przepływ ciepła w kierunku obszaru o niższej temperaturze, trwa on do chwili, gdy temperatury wyrównują się. Istnieją trzy sposoby przenoszenia ciepła: przez promieniowanie, konwekcję (unoszenie), oraz przez przewodzenie. Ten ostatni występuje w ciałach stałych.
Jeżeli w wyniku pewnych warunków przeciwległe ścianki pewnej płyty o powierzchni przekroju S i grubości d1, mają odpowiednio temperatury T1 i T2 (T1>T2), to następuje przepływ ciepła w kierunku powierzchni o niższej temperaturze.
Ilość ciepła przepływającego w jednostce czasu w stanie stacjonarnym wyraża się wzorem :
![]()
gdzie:
k - współczynnik przewodności cieplnej, oznacza ilość ciepła przechodzącego w jednostce czasu przez jednostkę powierzchni przy jednostkowym gradiencie temperatury (rożnica temperatury 1K przypada na jednostkę grubości).
Różne ciała mają różne wartości przewodności cieplnej. Ciała o małej wartości współczynnika przewodności cieplnej ![]()
nazywają się izolatorami termicznymi. Badana płytka, której współczynnik przewodności cieplnej k należy wyznaczyć, jest okrągła, w związku z czym zależność można napisać w postaci:
![]()
r1 - promień badanej płytki
Aby wyznaczyć współczynnik przewodności cieplnej płytki, należy zmierzyć jej grubość d1, promień r1, temperatury T1 i T2 przeciwległych powierzchni oraz ilość ciepła Q przechodzącą w jednostce czasu między powierzchniami o tych temperaturach.
Ta ilość ciepła jest bezpośrednio trudna do zmierzenia, dlatego też wyznacza się ją pośrednio metodą stygnięcia. Układ do wyznaczania przewodności cieplnej składa się z puszki mosiężnej o grubym dnie P1, płytki mosiężnej P2, płytki badanej P oraz ultratermostatu Hopplera.
Puszka, płytka badana i mosiężna są okrągłe. Mosiężna płytka P2 opiera się na trzech izolujących nóżkach, na niej jest położona badana płytka a następnie mosiężna puszka. Z ultratermostatu połączonego przewodami gumowymi jest ogrzewana puszka P1 , a następnie ciepło jest przewodzone przez płytkę P do płyty P2. W dnie puszki oraz w mosiężnej płycie znajdują się spojenia termopary w metalowych oprawkach. Układ płyt ogrzewa się do momentu ustalenia temperatury T1 górnej płyty (puszki) i temperatury T2 dolnej płyty. Można wówczas przyjąć, że temperatura górnej powierzchni badanej płytki równa jest temperaturze T1 puszki, a temperatura dolnej powierzchni badanej płytki jest równa temperaturze T2 dolnej płyty mosiężnej. Ustalenie się temperatur zachodzi wówczas, gdy ilość ciepła przewodzona przez badaną płytkę jest równa ilości ciepła wypromieniowanej przez dolną płytę. Aby określić tę ilość ciepła, należy wyznaczyć szybkość stygnięcia dolnej płytki w pobliżu temperatury T2. W tym celu po wyjęciu badanej płytki, ogrzewa się dolną płytę do temperatury T2 +5oC, a następnie po zdjęciu puszki wyznacza się szybkość jej stygnięcia jednakowych odstępach czasu (co 10 sek.) mierzy się temperaturę do chwili, gdy temperatura dolnej płyty będzie wynosiła T2 - 5oC.
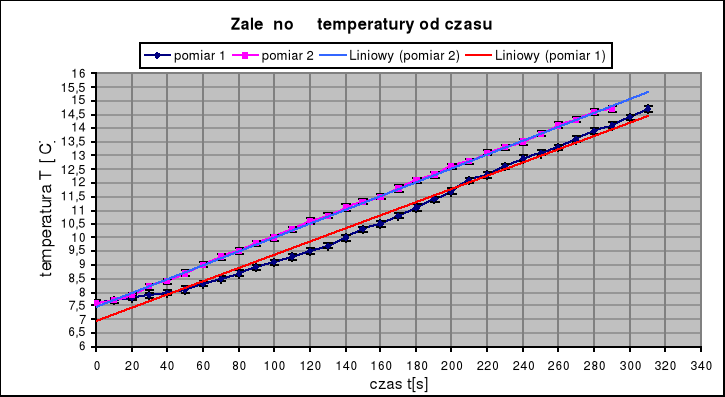
Przebieg chłodzenia należy przedstawić graficznie odkładając na osi rzędnych temperatury T, a na osi odciętych czas t. Z wykresu można określić szybkość stygnięcia ![]()
w pobliżu temperatury T2.
Jeżeli szybkość stygnięcia jest n, to ilość wypromieniowanego ciepła w jednostce czasu jest równa mcn , przy czym m oznacza masę mosiężnej płytki c - ciepło właściwe mosiądzu.
Zakładając, że ilość wypromieniowanego ciepła jest proporcjonalna do powierzchni, można wyrazić ilość ciepłą wypromieniowaną przez jednostkę powierzchni w jednostce czasu jako
![]()
gdzie
r- promień mosiężnej płytki
d- grubość mosiężnej płytki
Uwzględniwszy fakt, że po ustaleniu się temperatur ilość ciepłą przewodzona przez badaną płytkę jest równa ilości ciepła wypromieniowanej przez boczną i dolną powierzchnię mosięznej płyty, można napisać
![]()
stąd wzór obliczeniowy:
![]()
Wzór został wyprowadzony, przy założeniu, że strumień ciepła jest prostopadły do powierzchni badanej płytki. Warunek ten jest spełniony tylko częściowo.
![]()
III. Wyniki pomiarów.
pomiary zostały przeprowadzone dla płyty tekstolitowej w oparciu o wzór:
(*) ![]()
gdzie:
c - ciepło właściwe mosiądzu c = 375![]()
40 ![]()
m - masa mosiężnej płyty (odbiornika ciepła) m = 1,699![]()
0,002 [kg]
n - szybkość stygnięcia (zostanie wyznaczona na końcu ćwiczenia)
d1 - grubość badanej płyty d1 = 3,00![]()
0,01 [mm]
r - promień płyty mosiężnej r = 7,65![]()
0,01 [mm]
d - grubość płyty mosiężnej d = 12,20 ![]()
0,01 [mm]
r1 - promień badanej płyty r1 = 7,48![]()
0,01 [mm]
TS.r.- różnicowa temperatura stanu równowagi
Płyn w ultratermostacie ogrzano do temperatury 80 oC, a po ustaleniu się temperatur T1 i T2 - odczytano temperaturę różnicową TS.r.:
TS.r. = (T1 - T2) = (10,6![]()
0,1) oC
następnie podgrzano płytę mosiądzową o 3 oC (TS.r. = 7,6 oC) i notowano temperaturę stygnięcia tej płyty co 10 s, do TS.r. = 14,6 oC , pomiar przeprowadzono dwukrotnie
czas t mierzono stoperem z dokładnością 0,01 [s].
pomiar 1
Lp. |
t [s] |
T [oC] |
1 |
0 |
7,6 |
2 |
10 |
7,7 |
3 |
20 |
7,8 |
4 |
30 |
7,9 |
5 |
40 |
8,0 |
6 |
50 |
8,1 |
7 |
60 |
8,3 |
8 |
70 |
8,5 |
9 |
80 |
8,7 |
10 |
90 |
8,9 |
11 |
100 |
9,1 |
12 |
110 |
9,3 |
13 |
120 |
9,5 |
14 |
130 |
9,7 |
15 |
140 |
10,0 |
16 |
150 |
10,3 |
Lp. |
t [s] |
T [oC] |
17 |
160 |
10,5 |
18 |
170 |
10,8 |
19 |
180 |
11,1 |
20 |
190 |
11,4 |
21 |
200 |
11,7 |
22 |
210 |
12,1 |
23 |
220 |
12,3 |
24 |
230 |
12,6 |
25 |
240 |
12,9 |
26 |
250 |
13,1 |
27 |
260 |
13,3 |
28 |
270 |
13,6 |
29 |
280 |
13,9 |
30 |
290 |
14,1 |
31 |
300 |
14,4 |
32 |
310 |
14,7 |
pomiar 2
Lp. |
t [s] |
T [oC] |
1 |
0 |
7,6 |
2 |
10 |
7,7 |
3 |
20 |
7,9 |
4 |
30 |
8,2 |
5 |
40 |
8,4 |
6 |
50 |
8,7 |
7 |
60 |
9,0 |
8 |
70 |
9,3 |
9 |
80 |
9,5 |
10 |
90 |
9,8 |
11 |
100 |
10,0 |
12 |
110 |
10,3 |
13 |
120 |
10,6 |
14 |
130 |
10,8 |
15 |
140 |
11,1 |
Lp. |
t [s] |
T [oC] |
16 |
150 |
11,3 |
17 |
160 |
11,5 |
18 |
170 |
11,8 |
19 |
180 |
12,1 |
20 |
190 |
12,3 |
21 |
200 |
12,6 |
22 |
210 |
12,8 |
23 |
220 |
13,1 |
24 |
230 |
13,3 |
25 |
240 |
13,5 |
26 |
250 |
13,8 |
27 |
260 |
14,1 |
28 |
270 |
14,3 |
29 |
280 |
14,6 |
30 |
290 |
14,7 |
IV. Obliczenia i opracowanie wyników
wykres do wyznaczania szybkości stygnięcia n =
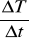
z pomiarów 1 i 2 wyznaczam współczynniki n1 i n2, a następnie n =
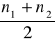
n = ![]()
![]()
[![]()
]
![]()
[![]()
]
![]()
[![]()
]
błąd bezwzględny n1 i n2 szybkości stygnięcia n1 i n2 wyznaczam metodą różniczki zupełnej:
![]()
[![]()
]
n2 = ![]()
[![]()
]
błąd bezwzględny n szybkości stygnięcia n wyznaczam tą sama metodą:
n = ![]()
[![]()
]
n = 0,0254![]()
0,0009 [![]()
]
obliczam współczynnik przewodności cieplnej ze wzoru:
![]()
![]()
[![]()
]
obliczam błąd względny pomiaru współczynnika przewodności cieplnej ze wzoru:
![]()
![]()
%
Uwaga: wszystkie wartości wraz z ich bezwględnymi błędami użyte w powyższym wzorze są podane na początku punktu III.Wyniki pomiarów.
k = ![]()
[![]()
]
k = (0,0211![]()
0,0039) [![]()
]
k = (0,0218![]()
18,38%) [![]()
]
V. Wnioski
Współczynnik przewodności cieplnej płyty tekstolitowej wynosi k = (0,0211![]()
18,38) % [![]()
], co oznacza, że jest rzędu 10-2, zatem badana płyta tekstolitowa jest izolatorem. Współczynnik ten został wyznaczony w oparciu o poprawność wzoru (*). Przy wyprowadzeniu tego wzoru założono warunek, że strumień ciepła jest prostopadły do powierzchni badanej płyty, co jest prawdziwe tylko w części ze względu na wypromieniowanie ciepła z brzegów badanej płytki. We wzorze jak i w samym ćwiczeniu ważną rolę odgrywa szybkość stygnięcia n, którego wartość rzeczywista może być inna od wyznaczonej, ponieważ prądy konwekcyjne mają większy wpływ na stygnięcie górnej płyty aniżeli dolnej. Otrzymany współczynnik jest obarczony względnie dużym błędem, który wyniósł 18,38 %. Duża część tego błędu została wniesiona przez błąd względny związany z ciepłem właściwym mosiądzu, którego wartość jest w przybliżeniu równa 10 %. Duży wpływ na dokładność pomiaru współczynnika k miał także błąd wyznaczenia szybkości stygnięcia n, jego wartość jest rzędu 1%. Błąd ten jest pośrednio związany z dokładnością odczytu temperatury z miliwoltomierza, dokładność ta wynosi 0,1 %.
Podsumowując można stwierdzić, iż dokładność tej metody wyznaczania współczynnika przewodności cieplnej jest dość dobra, pod warunkiem dysponowania dokładną wartością ciepła właściwego mosiądzu. W przeciwnym wypadku powyższa metoda może jedynie służyć do wyznaczenia rzedu wielkości badanego współczynnika i nie może służyć jako stała do dalszych badań laboratoryjnych.
Instytut Fizyki - Politechnika Wrocławska © 1998
- 3 -
t1
T1
t2
Wyszukiwarka
Podobne podstrony:
Fizyka- Pomiar przewodności cieplnej izolatorów.4, _________Andrzej G?rczak
Laboratorium Podstaw Fizyki spr 24 Pomiar przewodności cieplnej izolatorów, PWR, MATERIAŁY PWR 1, LA
Fizyka Pomiar Przewodności cieplnej izolatorów
Pomiar przewodności cieplnej izolatorów
POMIAR PRZEWODNOSCI CIEPLNEJ IZOLATORÓW 1(1) DOC
Fizyka Pomiar przewodności cieplnej izolatorów 2 DOC
Fizyka Pomiar przewodności cieplnej izolatorów 1 DOC
Fizyka Pomiar przewodności cieplnej izolatorów 3 DOC
5 Pomiar przewodności cieplnej izolaorów
pomiar przewodności cieplnej i elektrycznej metali
Wyznaczanie współczynnika przewodnictwa cieplnego, FIZYKA-sprawozdania
Pomiar przewodnictwa cieplnego, Przewodnictwo cieplne
5 Pomiar przewodności cieplnej izolaorów
Wyznaczanie współczynnika przewodnictwa cieplnego, Studia pomieszany burdel, FIZA EGZAMIN, FIZYKA-sp
POMIAR TEMPERATURY PIROMETREM OPTYCZNYM, MIBM WIP PW, fizyka 2, laborki fiza(2), 38-Badanie przewodn
więcej podobnych podstron