15.11.208

„Szereg czasowy”

y₁; y₂; y₃; ...; y_n

Jest to szereg szczegółowy, uporządkowany ze względu na czas, który reprezentują kolejne numery: 1, ..., n

y_t to wartość badanej cechy w okresie lub momencie „t”

Wskaźnik dynamiki (indexy)

y_b to wartość cechy w okresie badanym

y₀ to wartość cechy w okresie bazowym, podstawowym (branym jako pkt. odniesienia)

Interpretacja:

i>100% oznacza wzrost wartości cechy w okresie badanym w porównaniu z okresem podstawowym o i-100%

i=100% oznacza brak zmiany w okresie badanym w porównaniu z okresem podstawowym

i<100% oznacza spadek wartości cechy w okresie badanym w porównaniu z okresem podstawowym o 100%-i

Rodzaje indeksów:

• o podstawie stałej (okresem bazowym jest y₁)

pokazują zmiany w kolejnych okresach (momentach) w porównaniu z okresem (momentem) podstawowym jest ich „n” tj. tyle ile elementów szeregu czasowego.

• łańcuchowe

pokazują zmiany w kolejnych okresach (momentach) czasu w porównaniu z okresem (momentem) poprzednim (jest ich n-1) tj. brak jest pierwszego.

Średnie tempo zmian

to średnia geometryczna z indeksów łańcuchowych, którą w skrócie można zapisać jako:

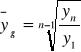
określa przeciętną zmianę wartości cechy okresu (momentu) za okres (moment):

jeśli
to oznacza przeciętny wzrost

jeśli
to oznacza przeciętny spadek

WIG

od 1993 roku jego wartość jest liczona według formuły kapitałowej

gdzie

M.(t) to wartość rynkowa (kapitalizacji) wszystkich spółek notowanych na giełdzie

M.(0) to kapitalizacja wszystkich akcji w dniu 16.04.1991 (pierwsza sesja giełdy, która wynosiła 57 140 000 starych złotych)

K(t) współczynnik korygujący dla okresu badanego

M.(t) cena akcji, ilość akcji, dywidenda, prawo poboru

Współczynnik korygujący uwzględnia prawo poboru i dywidendę

gdzie:

S(t) to skorygowana (o dywidendy i prawa poboru) wartość notowanych spółek

K(t -1) wartość współczynnika dla poprzedniej sesji. Przyjmuje się, że na pierwszej sesji (16.04.1991) jego wartość wynosiła K=1

Indexy indywidualne - pozwalają analizować zmiany cen (p.), ilości (q) i wartości (qp) pojedyńczych produktów.

• cen
  

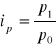
• ilości
  

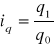
• wartości
  

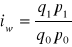
Indexy zespołowe (agregatowe)

pozwalają analizować zmiany wartości , cen oraz ilości zbioru (grupy produktów, wyrobów, artykułów ) które nie są jednorodne, np.: nabiał oznacza zarówno sery, mleko, jak i jaja mierzone w zupełnie inny sposób.

• wartości:
  

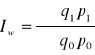
• ilości Laspeyresa:
  

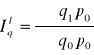
Mówią o przeciętnym wzroście (spadku) ilości określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że cena w okresie badanym była na poziomie z okresu podstawowego (cena stała).

• ilości Peaschego:
  

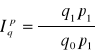
Mówi o przeciętnym wzroście (spadku) ilości określanego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że cena w okresie badanym była na poziomie okresu podstawowego (cena stała).

• cen Laspeyresa:
  

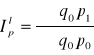
Mówi o przeciętnym wzroście (spadku) cen określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że ilość w okresie badanym była na poziomie z okresu podstawowego.

• cen Peaschego:
  

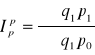
Mówi o przeciętnym wzroście (spadku) cen określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że ilość w okresie podstawowym była na poziomie z okresu badanego.

• ilości Fishera:
  

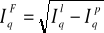
Mówi o przeciętnym wzroście(spadku) ilości określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym.

• cen Fishera:
  

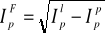
Mówi o przeciętnym wzroście (spadku) cen określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym.

---