Wydział Inżynierii Lądowej

Zespół 8

Chrzanowska Urszula

Fijoł Dominika

Głowacka Justyna

Sprawozdanie z ćwiczenia nr 10: Pomiar długości fal elektromagnetycznych metodami interferencyjnymi.

Spis treści

• Wstęp teoretyczny

Jednym z charakterystycznych zjawisk ruchu falowego jest interferencja, czyli efekt nakładania się fal. Fale mogą nakładać się w fazach zgodnych (wzmocnienie natężenia fali wypadkowej) lub w fazach przeciwnych (wygaszenie fali). Aby można było zaobserwować zjawisko interferencji, nakładające się fale muszą mieć taką samą częstotliwość oraz być spójne - czyli posiadać stałą w czasie różnicę faz.

Natężenie pola elektrycznego fali wyraża się wzorem: E=E₀sin(ωt + kx), gdzie
jest liczbą falową, a λ długością fali. Jeśli rozpatrujemy dwie spójne fale, z których jedna przebyła dłuższą drogę optyczną (x + Δ), uzyskujemy kąt przesunięcia fazowego
. Natężenie pola elektrycznego tej fali E=E₀sin(ωt + kx - φ).

Efekt nałożenia się dwóch fal opisuje wzór:

Po odpowiednich przekształceniach i podstawieniu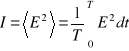
otrzymujemy wzór na natężenie fali wypadkowej:

,

gdzie I₁, I₂ są natężeniami fal składowych, a wyrażenie
opisuje efekt interferencji tych fal. Osłabienie natężenia otrzymamy, gdy
czyli
, a wzmocnienie, kiedy
czyli
.

• Pomiar długości fali elektromagnetycznej za pomocą interferometru Fabry-Perota

1. Zasada działania

W interferometrze Fabry-Perota fale elektromagnetyczne przechodzą przez 2 równoległe płytki przepuszczające część promieniowania, część zaś odbijające.

Rysunek 1: Schemat interferometru Fabry-Perota.

Pomiędzy falą przenikającą bezpośrednio przez płytki a falą dwukrotnie odbitą od ścianek powstaje różnica dróg Δ=2d cosα, gdzie d jest odległością między płytkami, a α kątem między prostą prostopadłą do płytek a kierunkiem padającej wiązki fal. Ze wzoru wynika, że zmieniając odległość między płytkami d, zmieniamy różnicę dróg optycznych Δ. Poszukiwana długość fali elektromagnetycznej wynosi
, gdzie r jest liczbą zaobserwowanych wzmocnień fali pomniejszoną o 1, d_m odległością między płytkami dla pierwszego zaobserwowanego wzmocnienia, a d_m+r odległością między płytkami dla ostatniego wzmocnienia.

2. Wyniki doświadczenia

Pomiar długości fal elektromagnetycznych metodą Fabry-Perota wykonano przy użyciu dwóch układów pomiarowych.

Rysunek 2: Schemat układu pomiarowego z interferometrem Fabry-Perota.

Pomiar wykonano przy ustawieniu płytek pod kątem α=10°±2° (
±
).

Tabela 1: Wyniki pomiaru interferometrem Fabry-Perota.

r=	Odległość między płytkami d [mm]	Błąd pomiaru odległości Δd [mm]
0	5	±2 (błąd jest wynikiem niepewności odczytu, wahań wskazówki woltomierza i błędu przyrządu pomiarowego (linijki))
1	26
2	43
3	62
4	79
5	96












Rysunek 3: Schemat układu pomiarowego dla fal odbitych od zwierciadła.

Tabela 2: Wyniki pomiaru dla fal odbitych od zwierciadła.

r=	Odczyt na linijce d [mm]	Błąd pomiaru odległości Δd [mm]
0	102	±5 (błąd jest wynikiem niepewności odczytu, wahań wskazówki woltomierza, błędu przyrządu pomiarowego (linijki) oraz błędu przyłożenia przyrządu pomiarowego)
1	120
2	137
3	154
4	170
5	187
6	204
7	222
8	239
9	255
10	271
11	289
12	305
13	323
14	339
15	356
16	372
17	390
18	408
19	425














• Pomiar długości fali elektromagnetycznej za pomocą interferometru Michelsona

1. Zasada działania

Rysunek 4: Zasada interferometru Michelsona.

W interferometrze Michelsona fale emitowane przez źródło padają na płytkę półprzepuszczalną. Część promieniowania przechodzi przez płytkę, a część zostaje odbita. Wiązka przepuszczona pada na zwierciadło i po odbiciu wraca tą samą drogą, odbija się od płytki i pada na detektor. Wiązka pierwotnie odbita od płytki pada na zwierciadło, odbija się, przechodzi przez płytkę i pada na detektor. Występuje różnica dróg optycznych obu wiązek. Zmieniając położenie jednego zwierciadła, zmieniamy różnicę dróg przebytych przez wiązki fal. Przesunięcie zwierciadła o wartość δ powoduje zmianę długości drogi optycznej odbitej od niego wiązki o 2δ. Długość fali elektromagnetycznej opisuje wzór:




Rysunek 5: Schemat interferometru Michelsona.

2. Wyniki doświadczenia

Tabela 3: Wyniki pomiaru interferometrem Michelsona.

r=	Odczyt na linijce d [mm]	Błąd pomiaru odległości Δd [mm]
0	604	±2 (błąd jest wynikiem niepewności odczytu, wahań wskazówki woltomierza i błędu przyrządu pomiarowego (linijki))
1	621
2	637
3	652
4	668
5	684
6	699
7	715
8	726
9	742
10	757
11	773
12	788
13	804
14	820
15	836
16	850
17	866
18	882














• Pomiar długości fali elektromagnetycznej przy użyciu siatki dyfrakcyjnej

1. Zasada działania

Rysunek 6: Siatka dyfrakcyjna

Siatka dyfrakcyjna to układ N równoległych do siebie szczelin rozmieszczonych w równych odstępach. Siatkę dyfrakcyjną charakteryzuje stała siatki (d), będąca sumą szerokości szczeliny (a) i odstępu między szczelinami (b).

Różnica dróg fal biegnących od dwóch sąsiednich szczelin
, gdzie α jest kątem ugięcia. Długość fali elektromagnetycznej wyraża się wzorem:




Rysunek 7: Schemat układu pomiarowego z siatką dyfrakcyjną

2. Wyniki doświadczenia

Zmierzono szerokość siatki dyfrakcyjnej D=880±1 mm.







Tabela 4: Wyniki pomiaru z siatką dyfrakcyjną.

m	Kąt ugięcia αm [radiany]	Błąd pomiaru kąta Δαm
1l		± (błąd wynika z niepewności odczytu, błędu przyrządu pomiarowego oraz błędu konstrukcji układu)
2l
1p
2p



















• Wnioski

W wykonywanym ćwiczeniu poznaliśmy cztery metody badania długości fal elektromagnetycznych, były to metody: interferometru Fabry-Perota, dla fal odbitych od zwierciadła, interferometru Michelsona oraz siatki dyfrakcyjnej.

Po wykonaniu ćwiczenia i dokonaniu obliczeń możemy stwierdzić, że najdokładniejszą metodą pomiaru jest metoda Michelsona, błąd wynosi w jej przypadku 2,2%, natomiast najmniej dokładna metodą okazała się metoda dla fal odbitych od zwierciadła (21,1%). Oczywistym wnioskiem jest zależność dokładności wyniku od liczby pomiarów - dzięki dużej liczbie pomiarów otrzymaliśmy dokładniejszy wynik (mniejszą niepewność pomiaru) oraz od przyjętych błędów cząstkowych, które wynikały głównie z niepewności odczytu, błędów przyrządów pomiarowych oraz błędów konstrukcji układów.

8

---