1. PODSTAWY RACHUNKU MACIERZOWEGO.
Niech dane będą liczby: a, b, c, d.
Liczbę a d - b c zapisujemy w postaci:
![]()
i nazywamy wyznacznikiem liczbowym stopnia II, czyli:
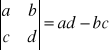
np. 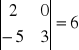
Wyznacznikiem stopnia ![]()
nazywamy liczbę:
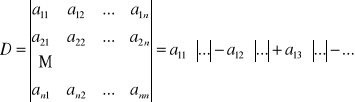
Dla wyznaczników stopnia III stosuje się wzór:
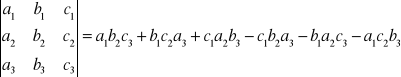
Transpozycją wyznacznika D nazywamy wyznacznik DT :
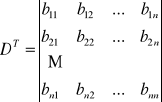
gdzie: bik = aki i, k = 1, 2, 3, ….. n
np. dla :

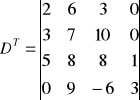
Def.1. Transpozycja wyznacznika nie zmienia jego wartości tzn. D = DT.
Def. 2. Zamiana miejscami dwóch dowolnych wierszy (kolumn) wyznacznika D powoduje
zmianę znaku tego wyznacznika.
Def. 3. Jeżeli wyznacznik ma dwa jednakowe wiersze (kolumny) to jest on równy 0.
Def. 4. Aby pomnożyć wyznacznik przez liczbę, należy przez tę liczbę pomnożyć dowolny
jeden jego wiersz albo jedną jego kolumnę.
Def. 5. Wyznacznik mający pod (nad) główną przekątną same zera jest równy iloczynowi
elementów głównej przekątnej.
Def. 6. Wyznacznik jest równy 0, jeżeli wiersze (kolumny) są liniowo zależne.
np. 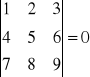
Def. 7. Wyznacznik o dwóch proporcjonalnych wierszach (kolumnach) = 0.
Def. 8. Wyznacznik mający wiersz (kolumnę) zerową = 0.
2. UKŁADY RÓWNAŃ LINIOWYCH.
Weźmy pod uwagę układ równań:
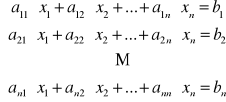
gdzie aik i bi są liczbami rzeczywistymi (zespolone),
x1 x2 … xn - szukane niewiadome
Def. 1. Rozwiązaniem układu nazywamy każdy uporządkowany układ liczb:
które wstawione w miejsce niewiadomych do lewych stron układu równań zamieniają wszystkie te równania w prawdziwe równości liczbowe.
Def. 2. Jeżeli układ ten posiada przynajmniej 1 rozwiązanie to nazywamy go układem zgodnym.
Jeżeli rozwiązań tych jest nieskończenie wiele to układ nazywamy nieoznaczonym
( jeśli posiada dokładnie 1 to nazywamy go układem oznaczonym ).
Jeżeli układ nie posiada ani jednego rozwiązania to układ jest sprzecznym.
Tw. Cramera.
Układ Cramera posiada dokładnie 1 rozwiązanie dane wzorami:
![]()
![]()
….. ![]()
Przykład.
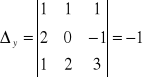
Rozwiązać układ równań:
x - 2y + z = 1
2x + y - z = 0
x - y + 3z = 2
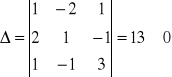
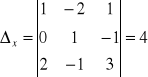
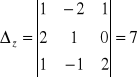
![]()
![]()
![]()
3. MACIERZE.
Macierzą A nazywamy układ m x n liczb rzeczywistych lub zespolonych zgrupowanych w tablicę:
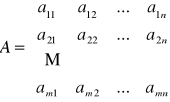
gdzie: m - ilość wierszy; n - ilość kolumn
Jeżeli n = 1 to macierz składa się tylko z jednej kolumny i nazywa się wektorem kolumnowyn.
Dla m = n macierz A nazywamy macierzą kwadratową.
Jeżeli det A = 0 to macierz kwadratowa A nazywa się osobliwą.
Jednym z rodzajów macierzy kwadratowych są macierze przekątniowe (diagonalne), które mają wartości różne od zera tylko na głównej przekątnej, np.:
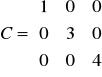
Natomiast szczególnym przypadkiem macierzy A jest macierz jednostkowa An stopnia n określona wzorem:
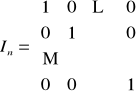
Macierze A i B są sobie równe (A = B), jeśli ich wszystkie wyrazy są równe: aij = bij .
Iloczyn macierzy A i liczby ![]()
jest macierzą ![]()
.
Suma dwóch macierzy o takich samych wymiarach C = A + B jest macierzą o elementach:
cij = aij + bij .
Iloczyn dwóch macierzy A (m x p) i B (p x n) jest macierzą C (m x n) o elementach obliczonych ze wzoru:
cij = aik + bkj .
Uwaga: ![]()
Transpozycją AT macierzy A nazywamy macierz, której wiersze są kolumnami macierzy A.
Macierz trójkątna ma postać:
(dolna) 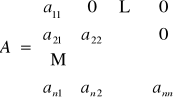
(górna odwrotnie)
Wyznacznik macierzy kwadratowej A stopnia n ma symbol:
det A = det 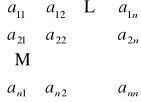
Tw. o istnieniu macierzy odwrotnej.
Jeżeli macierz kwadratowa A jest nieosobliwa, tzn. ![]()
to macierz do niej odwrotna istnieje i wyraża się wzorem:
![]()
gdzie: AD - macierz minorów.
Weźmy pod uwagę układ równań:
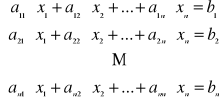
czyli:
A = 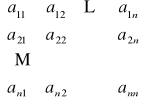
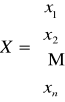
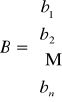
otrzymamy:
![]()
![]()
i wyznaczając macierz odwrotną A-1 otrzymamy wektor rozwiązań:
![]()
Przykład.
Rozwiązać metodą macierzową:
x + y + z = 1
x - y + 2z = 0
2x + y - z = -1
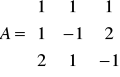

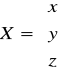
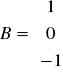
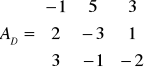
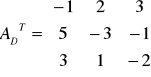
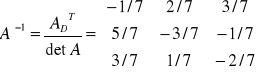
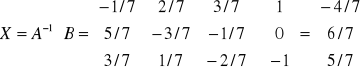
czyli:
x = -4 / 7 ; y = 6 / 7 ; z = 5 / 7
Praca domowa: zrobić w Excelu: - obl. detA; A-1. (5x5)
METODY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH.
Rozpatrujemy układ równań liniowych postaci:
![]()
gdzie:
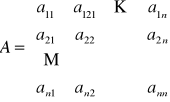
- jest n x n wymiarową macierzą,
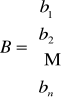
- danym wektorem,
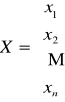
- szukanym rozwiązaniem.
Przykład.
Rozwiązać obwód prądu stałego pokazany na rysunku metodą oczkową:
Dane:
E1=20V; E2=40V; E3=10V; E5=20V;
R1=1 R2=2 R3=4; R4=R5=10
Równania oczkowe obwodu elektrycznego dla prądu stałego mają postać:
![]()
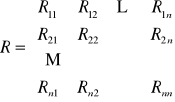
- macierz rezystancji oczkowych
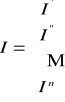
- wektor prądów oczkowych
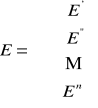
- wektor sum napięć źródłowych
W metodzie oczkowej przy znanej macierzy rezystancji oczkowej i wektorze wymuszeń, celem analizy jest znalezienie wartości prądów oczkowych.
Układ równań algebraicznych liniowych rozwiązuje się jedną z metod numerycznych.
Przy wprowadzaniu danych wejściowych stosuje się regułę metody oczkowej:
rezystancje własne oczek R11; R22; ... Rnn przedstawia się zawsze ze znakiem „plus”,
przy rezystancji wzajemnej Rkl wstawiamy znak „plus” gdy zwroty prądów oczkowych
Ik ; Il są w gałęzi wspólnej zgodne.
Gdy oczka k; l nie mają wspólnej gałęzi to Rkl=0.
napięcia źródłowe sumuje się dla danego oczka ze znakiem „plus” gdy zwrot napięcia jest zgodny ze zwrotem prądu oczkowego.
A zatem otrzymamy:
R11=R1+R2=3 R12= -R2= -2
R22=R2+R3+R5=16 R13= 0
R33=R3+R4=14 R23= -R3= -4
![]()
![]()
![]()
czyli:
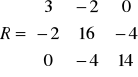
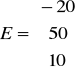
Wartości prądów oczkowych wynoszą:
![]()
R4
R1
R2
R5
R3
E5
E3
E1
E2
Wyszukiwarka
Podobne podstrony:
Zadanie 2 Met Num TM 2010, Politechnika Radomska, 1 stopień, przed 5 semestrem, metody numeryczne,
kompprot, Politechnika Radomska, 1 stopień, przed 5 semestrem, TeoriaObwodow, laborki
laboratorium(1), Politechnika Radomska, 1 stopień, mieszane
Protokół+wrp+-+na+zaliczenie, Politechnika Radomska, 1 stopień, mieszane
mechanika.teoria (1), Politechnika Łódzka, Inżynieria Środowiska, Semestr 2, Mechanika
Ferrorez napięć i prądów t, Politechnika Radomska, 1 stopień, mieszane, Różne
ekoinżynieria-teoria, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Ekoinzynieria środo
wydyma teoria, Politechnika Poznańska ZiIP, III semestr, wydyma egzam
ELPOL + zadania na ratynśką, Politechnika Radomska, 1 stopień, mieszane
Badanie transformatora 1 fazowego t, Politechnika Radomska, 1 stopień, mieszane, Różne
Badanie transformatora 1 fazowego p, Politechnika Radomska, 1 stopień, mieszane, Różne
Ferrorez napięć i prądów p, Politechnika Radomska, 1 stopień, mieszane, Różne
Zaliczenie, Politechnika Radomska, 1 stopień, mieszane, Różne
Kompensacja mocy biernej p, Politechnika Radomska, 1 stopień, mieszane, Różne
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
mechanika - teoria, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałó
METODYKA OPRACOWYWANIA WYNIKÓW POMIAROWYCH, MET0DYKA-spr., POLITECHNIKA RADOMSKA
Metrologia-lab-Metodyka opracowań wyników pomiarowych, METPOM S, POLITECHNIKA RADOMSKA
więcej podobnych podstron