ADAPTACJA PROGRAMU NAUCZANIA MATEMATYKI

DLA KLAS TERAPEUTYCZNYCH

W ZASADNICZEJ SZKOLE ZAWODOWEJ

W ODNIESIENIU DO PLANU EDUKACYJNEGO

NAUCZYCIELA

Marlena Leśniak

WSTĘP

Praca w różnych zawodach i codziennym życiu wymaga od człowieka ciągłego rozwiązywania problemów matematycznych: liczenia, mierzenia i ważenia.

Rozwiązywanie różnorodnych zadań umożliwia opanowanie umiejętności dostrzegania problemów matematycznych. Matematyka uznawana jest za przedmiot sprawiający uczniom upośledzonym umysłowo oraz uczniom kształcących się w klasach terapeutycznych w zasadniczych szkołach zawodowych duże trudności.

To, co uczeń koduje i dekoduje jest mocno nasycone abstrakcją. Zapisywane w formie cyfr liczby, to złożone pojęcia. Pojęciami są znaki: + , - , < , > oraz schematy graficzne. Od ucznia wymagane jest operacyjne rozumowanie matematyczne, cechujące się wysokim stopniem abstrakcji.

Proces kształtowania pojęć wymaga umiejętności logicznego myślenia i ścisłego wyrażania myśli. Tymczasem uczniowie szkół specjalnych oraz klas terapeutycznych mają przede wszystkim upośledzoną zdolność myślenia abstrakcyjnego. Powoduje to, że pojęcia matematyczne są dla nich mgliste i niepełne.

Rozdział 1

Charakterystyka uczniów klas terapeutycznych

Liczne niepowodzenia i trudności w nauce u uczniów zrodziły konieczność dostosowania wymagań edukacyjnych w szkołach na odpowiednich etapach kształcenia.

Niepowodzenia szkolne to sytuacje, które charakteryzują się występowaniem wyraźnych rozbieżności między wymaganiami wychowawczymi i dydaktycznymi szkoły a postępowaniem uczniów oraz uzyskiwanymi przez nich wynikami nauczania. Przyczyny niepowodzeń mogą być bardzo różnorodne, np.: społeczno-ekonomiczne, dydaktyczne, biopsychiczne.

Dla potrzeb tejże młodzieży utworzono a szkołach zasadniczych klasy terapeutyczne, które dają szansę kontynuacji kształcenia i uzyskania kwalifikacji zawodowych.

Taką możliwość dało Rozporządzenie Ministra Edukacji Narodowej z dnia 7 stycznia 2003r. w sprawie zasad udzielania i organizacji pomocy psychologiczno-pedagogicznej w publicznych przedszkolach, szkołach i placówkach. (Dz. U. z 2003 r. Nr 11, poz. 114).

Na mocy tego rozporządzenia w szkołach dopuszcza się organizowanie klasy terapeutycznych. Klasy te organizuje się dla uczniów wykazujących jednorodne lub sprzężone zaburzenia, wymagających dostosowania organizacji i procesu nauczania do ich specyficznych potrzeb edukacyjnych oraz długotrwałej pomocy specjalistycznej.

Zajęcia w klasach terapeutycznych prowadzą nauczyciele właściwych zajęć edukacyjnych. Nauczanie w klasach terapeutycznych prowadzone jest według obowiązujących programów nauczania, z dostosowaniem metod i form ich realizacji do indywidualnych psychofizycznych i edukacyjnych potrzeb uczniów.

Klasy terapeutyczne organizuje się z początkiem roku szkolnego.

Do klas terapeutycznych, za zgodą organu prowadzącego szkołę, w ramach posiadanych środków, mogą uczęszczać uczniowie innych szkół, z uwzględnieniem przepisów art. 17 ust. 2-3a ustawy, o systemie oświaty z dnia 7 września 1991 r.

O objęciu ucznia nauką w klasach terapeutycznych decyduje Dyrektor Szkoły. Objęcie ucznia nauką w klasie terapeutycznej wymaga opinii publicznej poradni psychologiczno-pedagogicznej, w tym poradni specjalistycznej.

Nauka ucznia w klasach terapeutycznych trwa do czasu zlikwidowania opóźnień w uzyskaniu osiągnięć edukacyjnych wynikających z podstawy programowej lub złagodzenia bądź wyeliminowania zaburzeń stanowiących powód objęcia ucznia taką formą pomocy.

O zakończeniu nauki ucznia w klasie terapeutycznej decyduje dyrektor szkoły na wniosek rodziców lub wychowawcy klasy.

Podstawową jednostką organizacyjną w szkole z klasami terapeutycznymi jest oddział złożony z uczniów, którzy w jednorocznym kursie nauki uczą się wszystkich obowiązkowych zajęć edukacyjnych, określonych szkolnym planem nauczania.

Liczba uczniów w oddziałach klas terapeutycznych wynosi od 10 do 15. W uzasadnionych przypadkach, za zgodą organu prowadzącego, liczba uczniów w oddziałach może być niższa.

Nauczyciele prowadzący zajęcia w danym oddziale tworzą zespół, którego zadaniem jest w szczególności ustalenie dla danego oddziału zestawu programów nauczania z zakresu kształcenia ogólnego i programu nauczania w danym zawodzie, z uwzględnieniem korelacji kształcenia ogólnego i kształcenia zawodowego.

Nauka w szkole zasadniczej z klasami terapeutycznymi trwa 2 lub 3 lata, w zależności od programu nauczania dla danego zawodu. Szczegółową organizację każdego roku szkolnego określają wewnętrzne przepisy każdej szkoły.

Uczniowie uczęszczający do klas terapeutycznych charakteryzują się obniżeniem lub opóźnieniem sprawności intelektualnej.

Obniżenie sprawności intelektualnej polega na tym, iż do pewnego momentu rozwój intelektualny dziecka przebiegał prawidłowo, a wyniku określonego czynnika chorobowego ulega zahamowaniu, bądź nastąpiła regresja. Obniżenie może być czasowe lub trwałe. O obniżeniu ogólnym poziomu intelektualnego mówimy wówczas, gdy uległy obniżeniu wszystkie funkcje intelektualne, a gdy uległy obniżeniu tylko niektóre funkcje, mówimy o parcjalnym obniżeniu tychże funkcji.

Opóźnienie rozwoju intelektualnego wskazuje na to, że aktualny rozwój intelektualny dziecka nie odpowiada wiekowi życia jego rówieśników, jest on często spowodowany indywidualną różnicą w tempie dojrzewania umysłowego oraz istnieje prawdopodobieństwo, iż poziom ten osiągnie normę. Opóźnienie globalne obejmuje wszystkie sprawności intelektualne, parcjalne dotyczy tylko niektórych sprawności, np.: percepcji wzrokowej, wzrokowo-słuchowej, koordynacji wzrokowo-ruchowej, wyobraźni przestrzennej, mowy czynnej.

Do klas terapeutycznych uczęszczają także uczniowie upośledzeni umysłowo w stopniu lekkim.

Definicji upośledzenia umysłowego jest wiele, lecz sprowadzają się one do tego, iż jest to istotnie niższy od przeciętnego w danym środowisku globalny rozwój jednostki z nasilonymi równocześnie trudnościami w zakresie uczenia się i przystosowania, spowodowany we wczesnym okresie rozwojowym przez czynniki dziedziczne, wrodzone, nabyte po urodzeniu wywołujące trwale zmiany w funkcjonowaniu ośrodkowego układu nerwowego.

Trudności w nauce u absolwentów gimnazjów specjalnych wiążą się z tym, iż program szkół podstawowych i gimnazjalnych różni się w zasadniczy sposób od programu szkolnictwa masowego, jest ograniczony w swych treściach ze względu na specyfikę i obniżony poziom intelektualny uczniów.

Ponadto szkoły integracyjne, do których uczęszcza młodzież o specyficznych potrzebach edukacyjnych również dostosowują wymagania i treści programowe do potrzeb tychże uczniów.

Występuje wśród tych uczniów olbrzymie zróżnicowanie w poziomie intelektualnym, zaburzeniach i deficytach intelektualnych, tempie pracy i poziomie myślenia abstrakcyjnego.

Uczniowie uczęszczający do klas terapeutycznych kierowani są przez właściwą poradnię psychologiczno-pedagogiczną, na podstawie przeprowadzonych badań psychologiczno-pedagogicznych. Opinie te zawierają informacje o deficytach umysłowych oraz zawierają wnioski i zalecenia do pracy z uczniem.

Z opinii można dowiedzieć się, iż uczniowie charakteryzują się niskim potencjałem intelektualnym, co ogranicza możliwości osiągania sukcesów szkolnych.

Zaburzone są funkcje słowno-pojęciowe, dysponują ubogim zasobem słów i pojęć. Obniżone też są funkcje myślenia pojęciowego, operacyjnego, abstrakcyjnego oraz pamięci słuchowej. Stwierdza się również deficyty analizatora wzrokowego i często występujące wady wymowy.

W zakresie umiejętności matematycznych można stwierdzić, iż uczniowie mają zaburzenia myślenia arytmetycznego, nie opanowali działań na liczbach dziesiętnych, mają braki w opanowaniu podstawowych wiadomości i umiejętności sięgających poprzednich etapów edukacyjnych, niesamodzielność w rozwiązywaniu zadań tekstowych, braki w znajomości technik obliczeniowych.

Charakterystyczną cechą tych uczniów jest wolne tempo pracy, niesamodzielność wykonywania zadań, obniżony poziom wiadomości i umiejętności szkolnych. Rozwój intelektualny jest nieharmonijny, występuje różnica w funkcjonowaniu słownym i bezsłownym.

Rozdział 2

Program nauczania a plan dydaktyczny nauczyciela

Sporządzenie rocznego planu nauczania jest ważną czynnością nauczyciela. Podstawę opracowania stanowi program. Zawartym w programie hasłom nadaje się bardziej szczegółowy charakter, uwzględniając warunki pracy w danej klasie, a przede wszystkim takie czynniki, jak:

1. stopień zaawansowania uczniów w nauce,

2. rodzaje i zasób posiadanych środków dydaktycznych,

3. zakres i sposoby rozwinięcia poszczególnych haseł programu w odpowiednich rozdziałach podręcznika,

4. liczbę lekcji służącą powtórzeniom materiału, jego kontroli i ocenie.

Najczęściej stosowana metodą planowania rocznego, wg Cz. Kupisiewicza jest zbiór czynności obejmujących:

1. gruntowną analizę programu nauczania,

2. porównywanie treści poszczególnych haseł programowych ujętych w grupy tematyczne, z odpowiednimi rozdziałami i podrozdziałami podręcznika

3. opracowanie bilansu czasowego niezbędnego do realizacji tych grup tematycznych,

4. uzupełnienie harmonogramu pracy czynnościami związanymi z powtórzeniem materiału oraz z kontrolą i oceną wyników nauczania,

5. sporządzenie listy podstawowych wiadomości i umiejętności, które muszą być bezwzględnie opanowane przez uczniów.

6. ostatnia z wymienionych czynności ma znaczący wpływ na uzyskiwane przez nauczyciela wyniki pracy z uczniami. Znając bowiem konkretne cele, jakie mogą być osiągnięte w toku nauczania łatwiej możemy dobierać odpowiednie metody i formy organizacyjne oraz środki dydaktyczne zapewniające realizację celów.

Program nauczania ustala, jakie wiadomości, umiejętności i w jakiej kolejności uczniowie mają sobie przyswoić i zawiera następujące elementy:

1. wstęp czyli określenie podstawy programowej oraz słowo skierowane od autora

2. cele nauczania matematyki w zasadniczej szkole zawodowej,

3. układ materiału w 2-letniej zasadniczej szkole zawodowej,

4. układ materiału w 3-letniej zasadniczej szkole zawodowej,

5. orientacyjny przydział godzin,

6. treści szczegółowych celów edukacyjnych i procedury ich osiągania,

7. propozycję metod, form pracy oraz sposoby kontroli i oceny osiągnięć uczniów.

Celem kształcenia ogólnego jest zapewnienie wszystkim uczniom optymalnego do ich możliwości rozwoju intelektualnego. Podrzędnymi celami są:

1. zaznajamianie uczniów z podstawami usystematyzowanej wiedzy o przyrodzie, społeczeństwie, technice i kulturze w zakresie umożliwiającym rozumienie najważniejszych rzeczy, zjawisk, wydarzeń, procesów oraz operatywne posługiwanie się tą wiedzą,

2. rozwijanie zdolności i zainteresowań poznawczych uczniów, nauczenie krytycznego myślenia, uwagi, wyobraźni, pamięci, fantazji i różnorakich umiejętności praktycznych,

3. kształtowanie naukowego poglądu na świat, czyli spójnie logicznych poglądów i przekonań wyznaczających stosunek do świata oraz ukierunkowujących ich postępowanie

4. wdrażanie do samokształcenia, wyrabianie potrzeby stałego i systematycznego uzupełniania posiadanej wiedzy i umiejętności w drodze uczenia się pozaszkolnego,

5. zaznajamianie uczniów z naukowymi podstawami produkcji i organizacji pracy.

Celem kształcenia zawodowego w szkole są, oprócz wymienionych wyżej również:

1. wyposażenie w wiedzę i umiejętności zawodowe podstawowe dotyczące całej grupy zawodów pokrewnych oraz specjalistyczne niezbędne do wykonywania określonego zawodu,

2. rozwinięcie zainteresowań związanych z danym zawodem oraz wdrożenie ich do stałego podnoszenia kwalifikacji.

Cele nauczania uczniów z obniżoną i opóźnioną sprawnością intelektualną: są w zasadzie takie same jak wyżej wymienione ogólne i zawodowe, jednak przewiduje się dla nich bardziej zindywidualizowany tok nauki, specjalne traktowanie przez nauczycieli, pomoc specjalistów, rodziców i kolegów.

Praca nauczycieli z tymi uczniami musi zawierać wiele elementów poglądowych, znaczną indywidualizację, dobór odpowiednich środków dydaktycznych i zwolnienie tempa pracy. Wymagana jest również modyfikacja programów nauczania wszystkich przedmiotów w zakresie, których przebiega kształcenie

Celem nauczania matematyki w szkole zawodowej jest:

1. zapewnienie uczniom możliwie dobrego przygotowania do praktycznej nauki zawodu poprzez usystematyzowanie i ugruntowanie wiedzy matematycznej zdobytej w gimnazjum oraz rozszerzenie o dodatkowe treści, aby każdy absolwent zasadniczej szkoły zawodowej mógł kontynuować naukę w dwuletnim uzupełniającym liceum ogólnokształcącym lub trzyletnim technikum uzupełniającym umożliwiającym uzyskanie świadectwa dojrzałości po zdaniu egzaminu maturalnego,

2. wyposażenie uczniów w wiadomości i umiejętności matematyczne z zakresu danej specjalności,

3. wyposażenie uczniów w umiejętności rozwiązywania problemów matematycznych życia codziennego,

4. wykorzystanie wiedzy do rozumienia zjawisk przyrodniczych, społecznych, ekonomicznych i technicznych,

5. rozwijanie umiejętności odczytywania, analizowania i przedstawiania danych statystycznych z różnych źródeł,

6. kształcenie umiejętności logicznego rozumowania i wyciągania wniosków,

7. kształcenie umiejętności posługiwania się językiem matematycznym, podstawowymi pojęciami matematycznymi,

8. rozwijanie wyobraźni przestrzennej uczniów,

9. rozwijanie zdolności i zainteresowań uczniów.

Cele związane z wychowaniem realizowane na lekcjach matematyki w zasadniczej szkole zawodowej są następujące:

1. wyrabianie nawyku sprawdzania uzyskanych wyników i ewentualnej korekty błędów,

2. nauczanie dobrej organizacji pracy,

3. wyrabianie systematyczności i wytrwałości,

4. pobudzanie aktywności umysłowej uczniów i chęci zdobywania wiedzy,

5. wyrabianie nawyku precyzyjnego wykonywania czynności takich jak: mierzenie, odmierzanie, rysowanie, konstruowanie, wycinanie, składanie itd.,

6. kształcenie umiejętności pracy w grupie.

7. Ze względu na cykl kształcenia, dwu lub trzyletni w szkole zawodowej, dostosowuje się treści podstawy programowej do czasu trwania nauki.

Nauczanie matematyki w szkole zawodowej ma pewną specyfikę. Powinno być bardziej doświadczaniem, działaniem, niż zapamiętywaniem wiadomości teoretycznych. Ucząc w szkole zawodowej powinno brać się pod uwagę poniższe zasady:

1. jak najczęściej organizować uczniowi pracę samodzielną lub pracę w grupie. Bierna obserwacja jest najmniej skuteczną metodą nauczania,

2. trafnie dobierać metody aktywizujące, które pozwalają uczniom na głębsze angażowanie się w proces kształcenia, podnoszą atrakcyjność lekcji, budują relacje międzyosobowe nauczyciel-uczeń i uczeń-uczeń. Uczą odkrywać nowe rzeczy, pozwalają doświadczać, osiągać sukcesy, poznawać siebie,

3. większość uczniów reprezentuje typ uczenia się od praktyki do teorii, zatem uwzględnić należy to w treściach nauczania i doborze zadań i celów,

4. uczniowie szkół zawodowych pracują w taksonomii celów poznawczych, czyli odtwarzają wzory poznane wcześniej, więc muszą je najpierw dobrze przyswoić, należy więc troszczyć się o dokładność wszelkich zapisów matematycznych i rysunków, poprawność rozwiązań zadań, nazw, oznaczeń, co pozwoli uczniowi prawidłowo przyswajać wiadomości i rozwijać umiejętności,

5. należy rozwiązywać zadania rozwijające umiejętność argumentacji, przewidywania, weryfikacji, analizy, wnioskowania. Zadania powinny być proste, możliwe do rozwiązania dla ucznia szkoły zawodowej o obniżonej sprawności intelektualnej, gdyż kształtują myślenie przyczynowo-skutkowe, przydatne w życiu człowieka,

6. nauczanie i uczenie matematyki odbywa się poprzez rozwiązywanie zadań. Zadanie to podstawowe narzędzie edukacji matematycznej. Propozycje zadań podczas lekcji oraz do wykonania w domu powinny uwzględniać:

1. stopniowanie trudności,

2. indywidualne potrzeby edukacyjne uczniów,

3. różnorodne formy i umożliwiać realizację przyjętych celów kształcenia.

Należy również zadbać aby nie powstawały braki w opanowaniu wiedzy na poziomie podstawowym, gdyż generować będą następne zaległości, których uczeń samodzielnie nie pokona. Należy również zindywidualizować treści zadań dla uczniów sprawniejszych i słabszych.

7. na lekcjach matematyki należy dużo rozmawiać, używając prostego, poprawnego języka, słuchać, pytać i odpowiadać, gdyż buduje to w procesie kształcenia relacje nauczyciel-uczeń i odwrotnie.

W procesie kształcenia nie należy zapominać o wymiarze duchowym edukacji, który ma wpływ na aspekty wychowawcze szkoły. Wysoka jakość tych relacji jest potrzebna przede wszystkim uczniowi, aby w szkole wzrastał we wszystkich wymiarach człowieczeństwa. Należy zatem pamiętać, że im słabszy uczeń, mniej zdolny, ubogi materialnie, zaniedbany wychowawczo przez rodzinę i środowisko, doświadczony niepowodzeniem, bezradny wobec problemów, tym bardziej potrzebuje nauczyciela, jego walorów osobistych i kompetencji dydaktyczno - wychowawczych.

Uczniowie klas terapeutycznych wpisują się właśnie w zakreślony powyżej model; doświadczeni negatywnie z wielkimi problemami, nie tylko intelektualnymi, ale często materialnymi, co determinuje ich postawę

w stosunku do szkoły i nauczyciela.

W związku z powyższym przed nauczycielami tych szkół stoi ważne zdanie związane z troską o jakość swojej pracy. Praca nauczycieli będzie skuteczna, jeśli opierać się będzie na podstawowych założeniach praktycznych:

1. trzeba mieć głębokie przekonanie, że każdy uczeń szkoły zawodowej także z matematyki „coś" potrafi, ważne jest, aby to odnaleźć i uczniowi uświadomić,

2. wielu z tych uczniów ma obniżone poczucie wartości, zachwianą wiarę w swe możliwości, utrwaloną bezradność nie tylko intelektualną, należałoby zatem mądrze i cierpliwie stosować system nagród, zauważać małe sukcesy, postępy, okazywać radość, pokazać i zaangażować w siebie,

3. dostosować wymagania do ich możliwości, ale konsekwentnie i do końca, indywidualizować poziom oraz zakres wymagań, budować przekonanie, że sprawiedliwie, to nie zawsze tak samo, że inny to nie gorszy, a słabszy ma prawo do większej uwagi i pomocy ze strony wszystkich a szczególnie nauczyciela,

4. sposób rozumowania uczniów szkoły zawodowej jest często nielogiczny, ubogi w argumenty, rozumowanie jest proste, intuicyjne, praktyczne, oparte na doświadczeniu, należy takie rozumowanie włączyć w proces kształcenia i zaakceptować je,

5. należy również zaakceptować, że matematyka nie jest „najważniejszym” przedmiotem w szkole zasadniczej, lecz wspomagającym, a jej ważność podnosić poprzez pokazanie jej użyteczności w życiu codziennym i zawodowym.

Rozdział 3

Adaptacja programu dla klas terapeutycznych

Wg I. Gucewicz - Sawickiej na dobór treści nauczania matematyki mają wpływ postulaty dydaktyki ogólnej, gdzie na pierwszy plan wysuwa się kształcenie postaw twórczych młodzieży oraz dążenie do nauczania integrującego wiedzę ucznia.

Z. Krygowska wymienia 4 kryteria doboru treści nauczania ze stanowiska dydaktycznego:

1. naukowości - uwzględnianie pojęć, które uważane są w matematyce za podstawowe dla matematyki, jako nauki,

2. elementarności - rozumiana, jako dostępność,

3. optymalnej organizacji materiału nauczania - to postulat, by treści nauczania nie były zebrane w sposób encyklopedyczny, by zostały ułożone z pewnymi ideami przewodnimi,

4. zastosowań - dotyczy przydatności przyswajanej wiedzy z matematyki.

Mając na uwadze te kryteria dostosowywano program nauczania matematyki w szkole zasadniczej do planu dydaktycznego nauczyciela szkoły zasadniczej w klasach terapeutycznych. Zawiera on niezbędne treści kształcenia, które są warunkiem powodzenia w procesie edukacji zawodowej, ukierunkowany jest na rozwiązywanie zadań związanych z zawodem i życiem codziennym.

Matematyka, jako przedmiot wspomagający w kształceniu pomaga rozwiązywać problemy zawodowe oraz jest wspomagająca w uzyskaniu dyplomu kwalifikacji zawodowych.

Nauczanie matematyki jest sterowaniem procesu uczenia się, rozumiane jako organizowanie aktywnego i świadomego procesu uczenia się matematyki przez ucznia, kierowanie jego prawidłowym przebiegiem i kontrolowanie jego wyników.

Rodzaje aktywności w uczeniu się matematyki:

1. przyjmowanie i asymilowanie matematycznej wiedzy, przekazywanej w rozmaitych formach z różnych źródeł(wykład, książka, test, dyskusja)

2. rozwiązywanie typowych zadań z zastosowaniem podstawowych metod matematycznych

3. redagowanie, zapisywanie , ilustrowanie schematami treści matematycznych, ćwiczenia w posługiwaniu się językiem matematycznym

4. aktywność twórcza wykraczająca poza w/w czynności

W związku z tym główne problemy dydaktyczne odnoszące się do procesu nauczania to:

1)poszukiwanie najbardziej efektywnych sposobów i środków postępowania dydaktycznego przy organizowaniu każdego z tych rodzajów aktywności ucznia

2) poszukiwanie optymalnego doświadczenia ucznia i jego swobodnej aktywności matematycznej

3)poszukiwanie sposobów zharmonizowania tych rodzajów aktywności uczniów aby się wzajemnie uzupełniały i wzmacniały w skutecznym procesie uczenia się.

Rozdział 4

Testy sprawdzające stopień realizacji planu dydaktycznego

W celu oceny stopnia realizacji planu dydaktycznego stosuje się następujące rodzaje kontroli:

1. roczna - najczęściej stosowana poprzez sprawdziany, testy o charakterze praktycznym i teoretycznym, obejmuje duży zakres materiału,

2. okresowa-przyjmuje formę ustną, wyrywkowej kontroli, tzw. kartkówki,

3. ustna, wyrywkowa kontrola realizacji celów sformułowanych w planie lekcji jest z konieczności fragmentaryczna i nie pozwala stwierdzić czy wszyscy uczniowie osiągnęli cel.

Najczęściej stosowana kontrola stopnia realizacji celów w klasach terapeutycznych to kartkówki oraz testy śródroczne i końcowe.

W tabeli poniżej przedstawiono wyniki przeprowadzanych testów w klasie pierwszej

Tabela 1

Wyniki testów okresowych uczniów z klas terapeutycznych

Ilość uczniów	celujący	Bardzo dobry	dobry	dostateczny	dopuszczający	Niedostateczny
38	-	1	3	18	10	6

Z tabeli 1 wynika, że uczniów piszących było 38, kształcący się w zawodach: kucharz, sprzedawca, ślusarz, krawiec, cukiernik. Najwięcej ocen mieści się w przedziale: dostateczny - dopuszczający. Średnia ocen: uzyskana średnia ocen - 2,5.

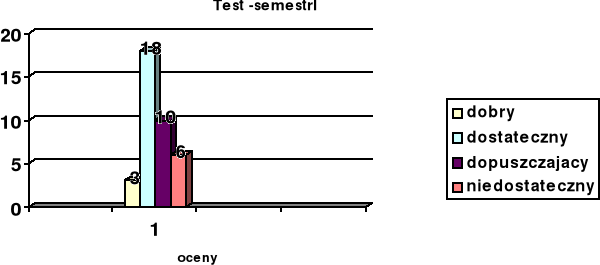
Tabela 2

Wyniki testów końcowych uczniów z klas terapeutycznych

Ilość uczniów	celujący	Bardzo dobry	dobry	dostateczny	dopuszczający	Niedostateczny
38	-	-	1	15	17	5

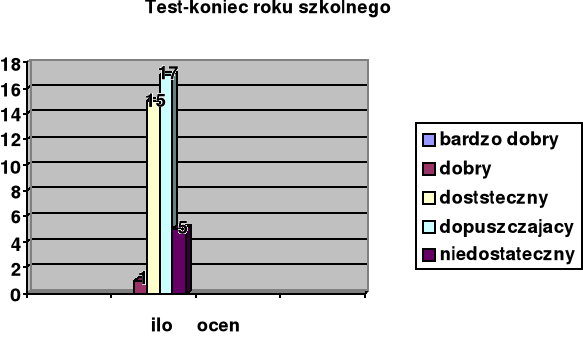
Wyniki testu przeprowadzonego po I semestrze w porównaniu z końcem roku szkolnego są wyższe, choć nie różnią się w zasadniczy sposób. Przyczyną różnic może być:

1. coraz trudniejszy materiał nauczania,

2. mała liczba godzin matematyki w szkole,

3. absencja uczniów,

4. łączenie zajęć praktycznych z nauką.

W minionym roku szkolnym uczniowie uczęszczali do klas terapeutycznych tylko na poziomie klasy pierwszej, gdyż zostały one powołane po raz pierwszy w roku szkolnym 2003/ 20004. Tak więc wyniki testów dotyczą tylko klas pierwszych.

Uczniowie klas terapeutycznych z powodzeniem uczestniczyli w konkursie matematycznym.

Podsumowanie

Nauczanie matematyki w klasach terapeutycznych dla uczniów o obniżonych zdolnościach intelektualnych jest procesem skomplikowanym i wymagającym twórczej postawy nauczyciela w przekazywaniu treści programowych.

Dużą rolę odgrywa motywowanie poprzez praktyczne zastosowanie zadań tekstowych, które dotyczą prawdziwych sytuacji życia codziennego, są jasno zredagowane i przedstawiają problem dla ucznia, który mógłby już na danym poziomie intelektualnym rozwiązać.

Uczniowie klas terapeutycznych w znaczącej większości deklarują chęć kontynuowania nauki w liceum uzupełniającym lub technikum, co powoduje konieczność realizacji wszystkich treści programu lecz obejmują one podstawowe wiadomości i umiejętności ze względu na ograniczone możliwości intelektualne uczniów.

Jednak aby dać możliwość sukcesu i powodzenia realizowane są w szkole konkursy szkolne i międzyszkolne, powodujące chęć zmierzenia się z innymi uczniami o podobnych problemach edukacyjnych oraz urealnienie samooceny.

Praca w tych klasach daje satysfakcję i pozwala mieć nadzieję, że uczniowie ci będą przygotowani do wykorzystania wiedzy matematycznej w życiu codziennym i będą potrafili znaleźć się na rynku pracy .

Literatura

1. Podstawy dydaktyki ogólnej, Czesław Kupisiewicz, PWN, 1982 r., Warszawa.

2. Podstawowe zagadnienia dydaktyki matematyki, pod redakcja Ireny Gucewicz - Sawickiej, PWN, 1882 r., Warszawa.

3. Wykłady o nauczaniu matematyki, Stefan Turnau, PWN, 1990 r., Warszawa.

4. Konwersatorium z dydaktyki matematyki, Wanda Nowak, PWN, 1989 r., Warszawa.

5. Program nauczania matematyki w zasadniczej szkole zawodowej, DKOS-4015-123/02, Urszula Łączyńska, REA s.j., 2002 r., Warszawa.

6. Matematyka dla każdego - podręcznik dla zasadniczej szkoły zawodowej- Urszula Łączyńska, REA s.j., 2002 r., Warszawa.

7. Upośledzenie umysłowe - pedagogika, pod redakcją Kazimierza Kirejczyka, PWN, 1981 r., Warszawa.

8. Matematyka. Poradnik dla nauczyciela i program w zasadniczych szkołach zawodowych., Leokadia E. Wojciechowska, WSiP, 2003r., Warszawa

21

---