3.3. Dynamika w ruchu po okręgu.

Kamień uwiązany na sznurku, poruszający się po okręgu

w płaszczyźnie poziomej.

Układ inercjalny:

Stała zmiana kierunku ruchu wynika z istnienia siły dośrodkowej, będącej sumą wszystkich sił działających na ciało.

w tym przypadku
- siła napinająca sznurek.

Układ nieinercjalny:

W tym układzie

Występuje siła bezwładności, równa co do wartości sile naciągu sznurka. Jest to siła odśrodkowa bezwładności.

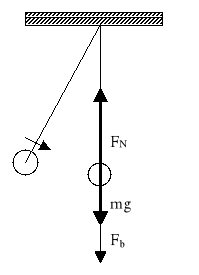
Wahadło matematyczne

Układ inercjalny:

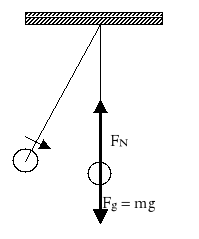
czyli F_d = F_N - F_g

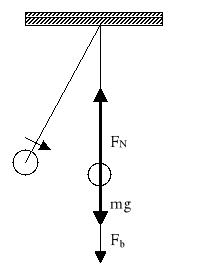
Z kolei dla układu nieinercjalnego:

czyli

F_N = F_g + F_b

co oczywiście jest identycznym wynikiem jak

obliczony w układzie inercjalnym.

3.4. Przyspieszenie i siła Coriolisa.

„Mrówka na płycie gramofonowej”

Mrówka porusza się względem płyty ruchem jednostajnym, prostoliniowym - wzdłuż promienia, z prędkością V_r . Płyta obraca się ze stałą prędkością kątową ω. Mrówka przemieszcza się z punktu A do punktu A' w czasie Δt. Prędkość styczna V_S rośnie wraz z odległością od środka płyty.

Prędkość V_S zmienia się od: V_S= ω⋅r do wartości V_S^l = ω⋅(r + Δr)

a więc ΔV_S = ω⋅(r + Δr) - ω⋅r

czyli ΔV_S = ω⋅Δr |:Δt

otrzymujemy:
dla Δt → 0
czyli a₂ = ω⋅V_r

ponieważ
oraz
są równoległe do
⇒ a_całk = a₁ + a₂ = 2ωV_r jest to przyspieszenie Coriolisa. Uwaga na zwrot wektora przyspieszenia - przeciwny do
!!

W obracającym się układzie odniesienia działa więc siła Coriolisa:

Jest to siła, która działa na ciało o masie m poruszające się ruchem postępowym z prędkością V w układzie odniesienia obracającym się z prędkością kątową ω.

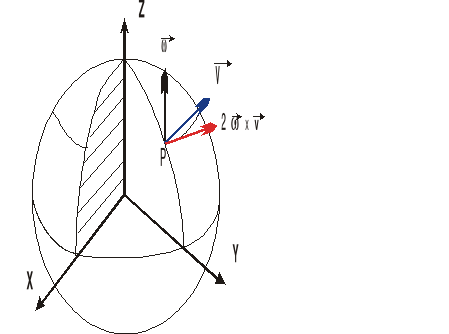
Ciało wyrzucone w punkcie P, na półkuli północnej, pionowo w górę z prędkością V, doznaje przyspieszenia Coriolisa stycznego do równoleżnika przechodzącego przez punkt P.

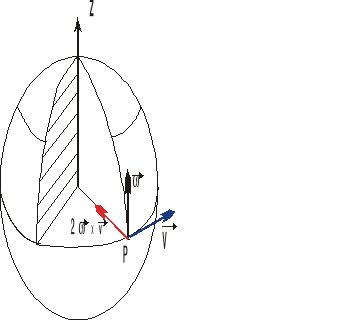
Z kolei ciało poruszające się z prędkością styczną do równoleżnika przechodzącego przez punkt P doznaje przyspieszenia Coriolisa skierowanego do środka Ziemi.

Inne przykłady:

• korekta torów rakiet balistycznych,

• podmywanie prawego brzegu rzek płynących w kierunku północnym wzdłuż południka

Opisując ruch w układzie inercjalnym:

=
+
+

przysp. w ukł. przysp. w ukł. przyspieszenie przyspieszenie

inercjalnym obracającym się Coriolisa dośrodkowe

Skoro ΔΦ jest małe to ΔV_r= V_r⋅ ΔΦ

czyli

dla Δt→ 0 można zapisać:

czyli a₁ =V_r ⋅ω

---