POLITECHNIKA GDAŃSKA

WYDZIAŁ BUDOWNICTWA LĄDOWEGO

KATEDRA MECHANIKI BUDOWLI

LABORATORIUM Z

MECHANIKI BUDOWLI

I WYTRZYMAŁOŚCI MATERIAŁÓW

TEMAT ĆWICZENIA :

WYZNACZENIE ŚRODKA ZGINANIA

Wykonała:

Katarzyna Danieluk

WBL, sem V, TOB

Opis ćwiczenia

Celem ćwiczenia było wyznaczenie środka zginania (lub ścinania) dwóch cienkościennych belek wspornikowych - o przekroju rurowym i kątowym

W obu przypadkach zakres czynności był jednakowy:

1. Ustawiono nieobciążoną szalkę w punkcie zerowym

2. Dokonano odczytów początkowych czujników zegarowych lewego f_L¹ i prawego f_P¹

3. obciążono szalkę odważnikami

4. Przesuwano szalkę w przedziale ⁺ 40 mm i notowano wskazania czujników f_L i f_P co 10 mm

5. Zdjęto odważniki

6. Ponownie ustawiono szalkę w punkcie zerowym i dokonano odczytów początkowych f_L² i f_P²

Doświadczenie 1 - przekrój rurowy

Wyniki pomiarów

f_L¹=2,16 mm f_P¹=3,04 mm

f_L²=2,13 mm f_P²=3,07 mm

Średnie odczyty początkowe:

f_L⁰=(f_L¹₊f_L²)/2=2,145 mm f_P²=(f_P¹+f_P²)/2=3,055

Ugięcia punktów L i P:

u_L=f_L-f_L⁰ u_P=f_P-f_P⁰

Kąt skręcenia belki:

=(u_L-u_P)/a ; a=200 mm

Tabela pomiarowa

Położenie	Wskazania	czujników	Ugięcie	punktów	Kąt skręcenia
siły [mm]	lewy fL	prawy fP	lewy uL	prawy uP	 [rad]
-40	0,56	4,18	-1,585	1,125	-0,01355
-30	0,84	3,74	-1,305	0,685	-0,00995
-20	1,17	3,25	-0,975	0,195	-0,00585
-10	1,48	2,81	-0,665	-0,245	-0,00210
0	1,79	2,35	-0,355	-0,705	0,00175
10	2,11	1,88	-0,035	-1,175	0,00570
20	2,42	1,45	0,275	-1,605	0,00940
30	2,73	1,01	0,585	-2,045	0,01315
40	3,03	0,59	0,885	-2,465	0,01675

Wykresy przemieszczeń punktów L i P przekroju w zależności od położenia siły.

Teoretyczne obliczenia środka zginania przekroju rurowego

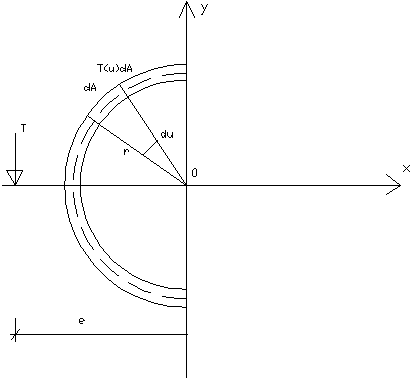
dA=r^.d^.δ

M₀=T^.e-
(dAr = 0

Zakładamy równomierny rozkład naprężeń stycznych  na powierzchni dA=δrd, ( jest wypadkową tego rozkładu.

T^.e-r²δ
(d(

Wyznaczenie funkcji (

(
x=0.5 r³δ

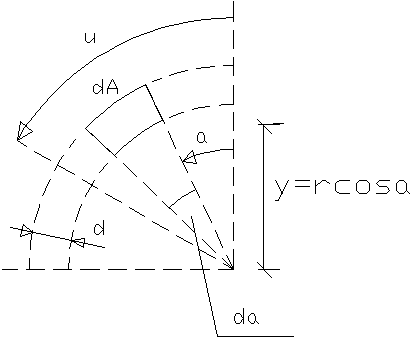
dA=r^.δ^d 
,

(

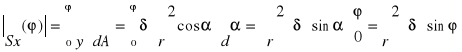
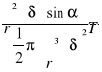
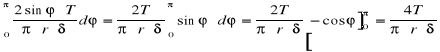
= -4,99 cm (r =3,92 cm)

Doświadczenie 2 - przekrój kątowy

Wyniki pomiarów

f_L¹=1,80mm f_P¹=0,95 mm

f_L²=1,81 mm f_P²=0,94 mm

Średnie odczyty początkowe:

f_L⁰=(f_L¹₊f_L²)/2=1,805 mm f_P²=(f_P¹+f_P²)/2=0,945

Ugięcia punktów L i P:

u_L=f_L-f_L⁰ u_P=f_P-f_P⁰

Kąt skręcenia belki:

=(u_L-u_P)/a ; a=200 mm

Tabela pomiarowa

Położenie	Wskazania	czujników	Ugięcie	punktów	Kąt skręcenia
siły [mm]	lewy fL	prawy fP	lewy uL	prawy uP	 [rad]
-40	0,66	1,77	-1,145	0,825	-0,00985
-30	0,89	1,53	-0,915	0,585	-0,00749
-20	1,13	1,28	-0,675	0,335	-0,00505
-10	1,37	1,05	-0,435	0,105	-0,00270
0	1,60	0,82	-0,205	-0,125	-0,00040
10	1,85	0,58	0,045	-0,365	0,00205
20	2,10	0,35	0,295	-0,595	0,00445
30	2,34	0,12	0,535	-0,825	0,00680
40	2,61	-0,10	0,805	-1,045	0,00925

Wykresy przemieszczeń punktów L i P przekroju w zależności od położenia siły.

Teoretyczne obliczenie środka zginania dla przekroju kątowego

y

7,5 cm

δ=0,35 cm

T₁ T

0 x

T₂

e_c

7,5 cm

-5,3 cm

Porównanie wyników otrzymanych doświadczalnie i teoretycznie

Przekrój pręta	Środek	zginania
	Wart. teoretyczna	Wart. doświadczalna
Rurowy	-4,99 cm	-4,98 cm
Kątowy	-5,30 cm	-5,34 cm

Położenie środka ciężkości przekroju poprzecznego

1. rurowego

δ  , cm

dA = r^.δ^d

x = r^.sin

r=3,92 cm

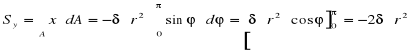
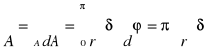
x_C = -2,495 cm

C(x_C;y_C)=C(-2,495 ; 0)

2. kątowego

δ = 0,35 cm

x_C=
cm

C(x_C;y_C)=C(-2,65 ; 0)

Kąt skręcania dla przypadku obciążenia siła przyłożoną w środku ciężkości

1. przekrój rurowy

C(-2,495 ; 0)

4,5 cm - 2,495 cm
2,0 cm - środek ciężkości znajduje się mniej więcej w

miejscu +20 mm na skali, dlatego też do obliczeń kąta skręcania bierzemy odczyty dla

położenia siły +20 mm

u_L= 0,275 mm

u_P= -1,675 mm

(0,275-(-1,675))/200= 0,00975 rad = 0,56^O

2. przekrój kątowy

C(-2,65 ; 0)

5,5 cm - 2,65 cm = 2,85 cm -środek ciężkości znajduje się pomiędzy

wartością +20 i +30 mm na skali , dlatego też wartości u_L i u_P wyznaczamy poprzez interpolację liniową

u_L= 0,499 mm

u_P= -0,791 mm

=(0,499-(-0,791))/200= 0,00645 rad = 0,37^O

---