SPRAWOZDANIE

Ćwiczenie 13: WYZNACZANIE ŚRODKA ZGINANIA

1. OPIS POSZCZEGÓLNYCH DOŚWIADCZEN

Celem ćwiczenia jest wyznaczenie środka zginania (lub ścinania) dwóch cienkościennych belek wspornikowych :

pierwszej - Belki o przekroju rurowym - ½ rury (doświadczenie 1)

drugiej - Belki o przekroju kątowym - kątownik (doświadczenie 2).

Doświadczenia wykonujemy przy pomocy dwóch zestawów odpowiednio dla poszczególnych doświadczeń . W skład każdego zestawu wchodzi:

• belka

• ruchoma szalka z odważnikami

• miarka umożliwiająca określenie położenia szalki

• czujniki zegarowe umożliwiające pomiar przemieszczeń

Przy pomocy odważników wywołujemy moment skręcający a na podstawie czujników dalej możemy wyznaczyć kąty skręcenia.

Doświadczenia rozpoczynamy i kończymy od pomiaru przemieszczeń na obu czujnikach przy nie obciążonym układzie. Przy wyznaczeniu kąta obrotu uśredniamy odczyty początkowe z czujników w celu wyeliminowania błędu .Następnie obciążamy układ i dokonujemy pomiarów przemieszczeń w zależności od położenia ciężarka. Następnie wykonujemy wykres funkcji ugięć w zależności od obciążenia . Punkt w którym proste z poszczególnych czujników się przecinają jest szukanym środkiem zginania .

Doświadczenie 1:

Na końcu pręta znajduje się szalka zamocowana prostopadle do pręta (1/2 rury). Na szalce znajduje się obciążenie równe 5kg co powoduje siłę P=5kg ≈ 5*9,81=49,05 N.

Doświadczenie 2:

Na końcu pręta znajduje się szalka zamocowana prostopadle do pręta (kątownik). Na szalce znajduje się obciążenie równe 5kg co powoduje siłę P=5kg ≈ 5*9,81=49,05 N.

2.WYNIKI POMIARÓW

2.1 PRZEKRÓJ 1/2 RURY (Belki o przekroju rurowym)

- Odczyty początkowe przy nieobciążonym układzie:

f_L¹ = 3,00 f_P¹= 4,90

- Odczyty końcowe przy nieobciążonym układzie:

f_L² = 2,98 f_P²= 4,86

- Średnie odczyty początkowe:

f_L⁰ = 0,5(f_L¹ + f_L² ) = 0,5 (3,00+2,98) = 2,99

f_P⁰= 0,5(f_P¹ + f_P²) = 0,5 (4,90+4,86) = 4,88

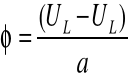
- Kąt skręcenia na podstawie otrzymanych wyników:

2.2 PRZEKRÓJ KĄTOWNIKA (Belki o przekroju kątowym)

- Odczyty początkowe przy nieobciążonym układzie:

f_L¹ = 2,40 f_P¹= 3,00

- Odczyty końcowe przy nieobciążonym układzie:

f_L² = 2,38 f_P²= 3,02

- Średnie odczyty początkowe:

f_L⁰ = 0,5(f_L¹ + f_L² ) = 0,5 (2,40+2,38) = 2,39

f_P⁰= 0,5(f_P¹ + f_P²) = 0,5 (3,00+3,02) = 3,01

- Kąt skręcenia na podstawie otrzymanych wyników:

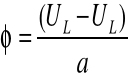
3. OBLICZENIA TEORETYCZNE

Środek zginania- punkt w którym należy przyłożyć siłę aby zredukować wypadkową naprężeń stycznych ( siła w tym punkcie nie wywołuje skręcania ) .

3.1 PRZEKRÓJ 1/2 RURY (Belki o przekroju rurowym)

R=3,92 cm

δ=0,27

dA=dSδ

dS=Rdϕ

dA=Rδdϕ

y=Rcosϕ

czyli:

∑ M_sO=0 , stąd :

T _x - ∫ dt R = 0

T _x - t R = 0 (1) t- wypadkowa naprężeń stycznych

τ = (S_x T)/(Ix δ) Ix-moment bezwładności przekroju: I_x = 0,5 Π R³δ

Sx-moment statyczny: S_x = ∫ y dA

S_x = ∫ R cosϕ R δ dϕ = ∫ R² δ cosϕ dϕ = R² δ cosϕ + c

Wiedząc , że dla: Sx (ϕ = 0) = 0 , stała c = 0 .

S_x = R² δ sinϕ .

τ = (R² δ sinϕ T)/( 0,5 Π R³δ δ) = ( 2 sinϕ T)/(R δ Π )

t = ∫ τ dA = ∫ (( 2 sinϕ T )/( R δ Π )) R δ dϕ = ( 2 T ) / Π [ - cosϕ ] = ( 2 T ) / Π [ - ( -1-1)] = 4 T / Π

Podstawiając do równania (1) , otrzymujemy :

T_x = (4 T / Π) R

x = ( 4/Π ) R = 4 (3,92/Π) = 4,99 cm

Zgodnie z przyjętym układem współrzędnych w doświadczeniu odległość od punktu zginania równa się :

e =4,50 - 4,99= -0,49cm

3.2 PRZEKRÓJ PIERŚCIENIOWY OTWARTY (Belki o przekroju kątowym)

Korzystam z warunku jak w 3.1:

∑ MsO=0 , stąd :

T_y x - T₁ a - T₂ a = 0 (2)

∑X = 0 , stąd :

T₁ = T₂

∑Y = 0 , stąd :

T_y = T₁ + T₂

podstawiając do równania (2)

(T₁ + T₂ ) x = (T₁ + T₂ ) a

x = a

Wiedząc , że a = 5,3 cm otrzymujemy : x = 5,3 cm .

Zgodnie z przyjętym układem wsp. w doświadczeniu odległość od punktu zginania równa się :

e = 5,50 - 5,30 = 0,20 cm.

4.PORÓWNANIE WYNIKÓW DOŚWIADCZEŃ Z OBLICZENIAMI TEORETYCZNYMI

RODZJ PRZEKROJU	WARTOŚĆ DOŚWIADCZALNA	WARTOŚĆ TEORETYCZNA
RUROWY	-6,5	-4,9
KĄTOWY	1,25	2,0

5.OBLICZANIE POŁOŻENIA ŚRODKA CIĘŻKOŚCI PRZEKROJU POPRZECZNEGO BELKI .

5.1 PRZEKRÓJ 1/2 RURY (Belki o przekroju rurowym)

R = 3,92 cm .

x = R sinϕ

A = ∫ R δ dϕ = R Π δ

Środek ciężkości S (X_c , Y_c) . X_c = S_y/A Y_c = S_x/A

Y_c = 0 ponieważ moment statyczny wzgl. osi X = 0 - przekrój monosymetryczny .

X_c = S_y/A

S_y = ∫ x dA

S_y = ∫ R sinϕ R δ dϕ

S_y = -R² δ cosϕ = -R² δ ( -1-1) = 2 R² δ

X_c = ( 2 R² δ )/( 2 Π δ ) = 2 R / Π = 2,496 cm

Zgodnie z przyjętym układem współrzędnych w doświadczeniu Xc = 4,50 - 2,496 = 2,004cm

5.2 PRZEKRÓJ PIERŚCIENIOWY OTWARTY (Belki o przekroju kątowym)

x = 2,65 cm .

A = 2 δ 7,5 = 5,25 cm² .

Środek ciężkości S (Xc , Yc) . Xc = Sy/A Yc = Sx/A

Yc = 0 ,ponieważ moment statyczny wzgl. osi X = 0 - przekrój monosymetryczny .

Xc = Sy/A

Sy = A x

Sy = 5,25 ∗ 2,65 = 13,91 cm³

Xc = 13,91/5,25 = 2,65 cm

Zgodnie z przyjętym układem współrzędnych w doświadczeniu Xc = 5,50 - 2,65 = 2,85cm

6. POMIAR KĄTA SKRĘCANIA DLA PRZYPADKU OBCIĄŻENIA SIŁĄ PRZYŁĄŻONĄ W ŚRODKU CIĘŻKOŚCI PRZEKROJU POPRZECZNEGO .

6.1 PRZEKRÓJ 1/2 RURY (Belki o przekroju rurowym)

U_L = 0,40

U_P = - 1, 34

ϕ = ( U_L - U_P )/a = (0,4+1,43)/200= 0,00915

6.2 PRZEKRÓJ PIERŚCIENIOWY OTWARTY (Belki o przekroju kątowym)

U_l = 0,55

U_p = -0,83

ϕ = ( U_l - U_p )/a = (0,55+0,83)/200= 0,0069

7.UWAGI WŁASNE

W wykonywanym ćwiczeniu zarówno w doświadczeniu nr 1 jak i w doświadczeniu nr 2 , wyznaczaliśmy środki zginania , czyli punkty w których należy przyłożyć siłę tnącą aby nie wywołała momentu skręcającego .Studiując wykresy funkcji ugięć w zależności od obciążenia znajdujemy punkt przecięcia się dwóch wykresów - jest to punkt w którym nie występuje skręcenie czyli nasz szukany punkt .

Położenie punktu wyznaczone doświadczalnie i teoretycznie różni się nieznacznie zarówno przy przekroju rurowym jak i kątowym . Różnicę tę upatrujemy:

- w niedokładności pomiarów - wiąże się to z niedokładnością przyrządów oraz błędnego

odczytania z czujników pomiarowych .

- niedokładnego naniesienia punktowo wykresu potrzebnego do określenia środka zginania

- niedokładnego odczytu położenia środka zginania z w.w. wykresu .

5

6

Wykonali :

Adam Julicki

Rafał Łupina

Michał Pieczywek

---