Dynamika punktu materialnego

Dynamika zajmuje się badaniem związku pomiędzy siłami działającymi na dany obiekt a ruchem tego obiektu.

Podstawą dynamiki punktu materialnego jest drugie prawo Newtona

gdzie:
- jest siłą działająca na punkt w danej chwili,

- jest przyspieszeniem tego punktu w tejże chwili względem inercjalnego układu odniesienia,

a
- jest masą tego punktu, o której zakładamy, że jest niezmienną względem czasu.

Na ogół siła
działająca na punkt zależy zarówno od położenia tego punktu jak i jego prędkości.

Inercjalny układ odniesienia? Mając na uwadze względność przyspieszenia punktu nie można się spodziewać, że tak sformułowane drugie prawo Newtona będzie spełnione w każdym układzie odniesienia. Wybór układu odniesienia zależy od rodzaju rozpatrywanego zagadnienia. W zagadnieniach dynamiki w otoczeniu Ziemi, jako układ inercjalny przyjmujemy dowolny nieruchomy względem Ziemi. W zagadnieniach podróży międzyplanetarnych jako układ odniesienia przyjmujemy dowolny nieruchomy względem Słońca, itd.

Zasada zachowania pędu punktu materialnego

Pędem punktu materialnego w danej chwili nazywamy wyrażenie

gdzie
- jest prędkością rozpatrywanego punktu materialnego w tejże chwili.

Pamiętając, że

i korzystając z założenia stałości masy, możemy drugie prawo Newtona przedstawić w postaci

co po scałkowaniu względem czasu w przedziale
daje

.

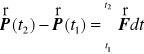
Wyrażenie
bywa nazywanie popędem siły
w przedziale czasowym
.

Zasada zachowania krętu punktu materialnego

Krętem (momentem pędu) punktu materialnego względem nieruchomego punktu A w danej chwili nazywamy wyrażenie

gdzie
- jest wektorem położenia rozpatrywanego punktu materialnego względem punktu A w tejże chwili.

Mnożąc wektorowo zasadę zachowania pędu

przez
otrzymujemy

.

Ale korzystając z reguły Leibnitza i właściwości iloczynu wektorowego mamy

.

Zatem

.

Wykazaliśmy, zatem, że prędkość zmian krętu względem punktu nieruchomego równa jest momentowi siły względem tego punktu.

Po scałkowaniu względem czasu w przedziale
daje to

.

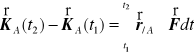
Zasada zachowania energii kinetycznej punktu materialnego

Energią kinetyczną punktu materialnego nazywamy wyrażenie

Po zróżniczkowaniu względem czasu otrzymujemy

Prawa strona
jest nazywana mocą siły
w danej chwili.

Po scałkowaniu względem czasu w przedziale
daje to

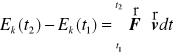
Prawa strona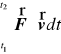
jest nazywana pracą siły
w przedziale
.

Zasada zachowania energii potencjalnej punktu materialnego

Z teorii całki krzywoliniowej wiadomo, że w przypadku, gdy siła
działająca na rozpatrywany punkt materialny zależy wyłącznie od położenia tego punktu i w taki sposób, że dla dowolnej krzywej łączącej dwa dowolne punkty A, B całka krzywoliniowa

nie zależy od drogi całkowania to możemy zdefiniować funkcję
taką, że

oraz

,
,
,
.

Wtedy taką funkcję
nazywamy potencjałem pola sił
, a wyrażenie

nazywamy energią potencjalną punktu materialnego.

Zakładając, że rozpatrywany punkt materialny znajduje się w polu sił potencjalnych oraz różniczkując energię potencjalną względem czasu otrzymujemy

.

Pochodną potencjału pola sił możemy obliczyć na zasadzie różniczkowania funkcji złożonej otrzymując

Zatem

Uwaga! Z teorii całki krzywoliniowej wynika również, że potencjalne pole sił spełnia warunek
i odwrotnie, jeżeli w obszarze jednospójnym pole sił spełnia warunek
to w tym obszarze jest ono potencjalne.

Przypadki szczególne równań ruchu punktu materialnego

Z punktu widzenia matematyki można prawa dynamiki punktu materialnego traktować jako układ zwyczajnych równań różniczkowych

,

względem nieznanych funkcji prędkości
oraz położenia
. Dla kompletności sformułowania problemu należy określić również warunki początkowe prędkości

i położenia

.

Na ogół zagadnienie takie nie posiada rozwiązań analitycznych i trzeba ich poszukiwać metodami numerycznymi. W szczególnych przypadkach budowy funkcji
rozwiązania analityczne mogą istnieć.

Siła jako znana funkcja czasu

Zakładamy, że
zależy od czasu w zadany sposób. Wtedy równanie ruchu punktu materialnego

scałkowane względem czasu w przedziale
daje

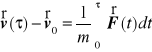
gdzie
oznacza początkową wartość prędkości. Całkując następnie definicję prędkości

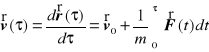
względem czasu w przedziale
otrzymujemy

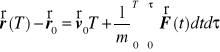
gdzie
oznacza początkową wartość położenia rozpatrywanego punktu.

Zauważmy, że otrzymaną całkę dwukrotną można przekształcić na jednokrotną używając metody całkowania przez części

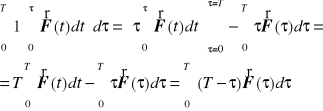
Zatem rozwiązanie równań ruchu w rozpatrywanym przypadku ma postać.

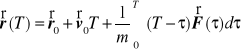
Widać, że do rozwiązania potrzebujemy warunków początkowych na położenie
oraz prędkość
.

Rzut ukośny

W przypadku szczególnym ruchu punktu w jednorodnym polu grawitacyjnym Ziemi zakładamy, że

gdzie
jest wektorem przyśpieszenia ziemskiego. Wtedy rozwiązanie równań ruchu punktu przyjmuje postać

,

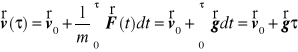
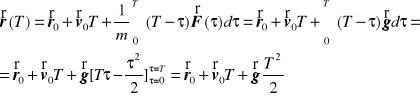
Rzut ukośny z uwzględnieniem oporu powietrza

Dla małych prędkości ruchu dobrym przybliżeniem zagadnienia jest założenie liniowości oporu powietrza względem prędkości. Wtedy przyjmujemy następujące wyrażenie dla siły działającej na punkt

i druga zasada dynamiki przyjmuje postać

.

Jest to niesprzężony układ 3 zwyczajnych niejednorodnych równań różniczkowych drugiego rzędu. Rozwiązanie ogólne równania jednorodnego ma postać

gdzie

.

Rozwiązanie szczególne znajdziemy metodą Cauchy

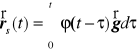
gdzie
jest rozwiązaniem równania jednorodnego, tzn.

spełniającym następujące warunki początkowe

,
.

Zatem

Z twierdzenia o pochodnej funkcji górnej granicy całkowania wynika, że dla rozwiązania szczególnego mamy

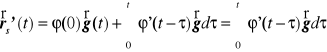
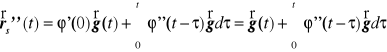
czyli lewa strona rozpatrywanego równania różniczkowego wynosi

.

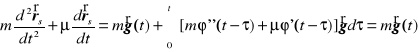
Zatem rozwiązanie szczególne wg. metody Cauchy spełnia rozważane równania różniczkowe z jednorodnymi warunkami początkowymi

,
.

Zatem rozwiazanie rozpatrywanego przypadku drugiego prawa Newtona ma postać

.

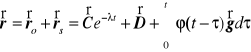
Do rozpatrzenia pozostały jeszcze warunki poczatkowe

,
.

Proste obliczenia dają natępujące wyniki

,
,
.

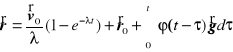
Korzystają z założenia stałości grawitacji otrzymujemy

.

Z własności funkcji wykładniczej wynika, że dla dużych wartości czasu
, a prędkość zbliża się do wartości
.

Drgania własne punktu materialnego

Załóżmy, że siła działajaca na punkt jest potencjalna i zależy liniowo od wychylenia punktu z położenia równowagi. Wtedy dobierając odpowiednio układ współrzędnych mamy

,
,

gdzie
,
i
są parametrami sprężystości podparcia punktu materialnego.

Dla składowej x wychylenia punktu mamy nastepujące równanie ruchu

.

Jego rozwiązanie ogólne ma postać

gdzie
.

Dla składowej x prędkości mamy zatem

.

Z warunków początkowych

,
.

obliczamy stałe całkowania

,
.

Ostatecznie otrzymujemy

.

Dla pozostałych składowych wychylenia jest analogicznie

,
.

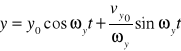
Drgania własne tłumione punktu materialnego

Załóżmy, że dodatkowo na punkt działa siła oporu proporcjonalna do prędkości wychylenia z położenia równowagi. Wtedy dobierając odpowiednio układ współrzędnych mamy

gdzie
jest parametrem tłumieniem. Druga zasada dynamiki ma zatem postać

co po uporządkowaniu daje następujące

jednorodne liniowe równanie różniczkowe 2go rzędu o stałych współczynnikach. Jego rozwiązania poszukujemy w postaci funkcji wykładniczych
z parametrem
spełniającym nastepujące równanie charakterystyczne

Jego pierwiastki zależą od wyróżnika
. W przypadku tzw. dużego tłumienia
wyróżnik jest dodatni

i oba pierwiastki są liczbami ujemnymi

a rozwiązanie równaia ruchu można przedstawić w postaci

,

Stałe całkowania wyznaczamy z warunków poczatkowych

,

otrzymując

,
.

Zatem

.

W przypadku tzw. tłumienia krytycznego
równanie charakterystyczne ma jeden pierwiastek podwójny

i rozwiazanie przyjmuje postać

,
.

Stałe całkowania wyznaczamy z warunków poczatkowych

,

otrzymując

,
.

Zatem

.

W przypadku tzw. małego tłumienia
równanie charakterystyczne ma pierwiastki zespolone

gdzie

,

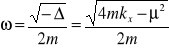
sąliczbami dodatnimi. Wtedy

Stałe całkowania wyznaczamy z warunków poczatkowych

otrzymując

Zatem

.

Drgania wymuszone punktu materialnego

Załóżmy, że dodatkowo na punkt działa harmoniczna siła wymuszająca o amplitudzie
i częstości
. Wtedy dobierając odpowiednio układ współrzędnych mamy

gdzie
jest parametrem tłumieniem. Druga zasada dynamiki ma zatem postać

co po uporządkowaniu daje następujące

niejednorodne liniowe równanie różniczkowe 2go rzędu o stałych współczynnikach. Jego rozwiązania poszukujemy w postaci sumy
rozwiązania ogólnego równania jednorodnego
i rozwiązania szczególnego
równania niejednorodnego. Rozwiązanie ogólne rozpatrzyliśmy w poprzednim paragrafie. Rozwiązanie szczególne znajdujemy metodą Cauchy

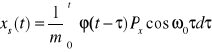
gdzie
jest rozwiązaniem równania jednorodnego, tzn.

spełniającym następujące warunki początkowe

,
.

Zauważmy, że rozwiązanie dla funkcji
możemy również wziąć z poprzedniego paragrafu.

W przypadku dużego tłumienia
z poprzedniego paragrafu znajdujemy

,
.

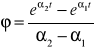
gdzie

,
,
.

Całkowanie we wzorze Cauchy daje następująca postać rozwiązania szczególnego

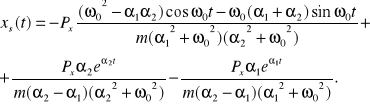
Z ujemności pierwiastków równanie charakterystycznego wynika, że dla dużych wartości czasu równanie drgań ma postać

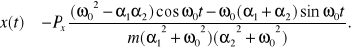
W przypadku tłumienia krytycznego
otrzymujemy

,

gdzie

.

Dla rozwiązania szczególnego otrzymujemy wtedy

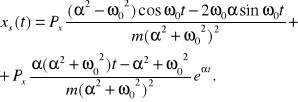
Dla dużych wartości czasu równanie drgań przyjmuje postać

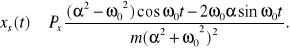
W przypadku małego tłumienia
otrzymujemy

,

gdzie

,
.

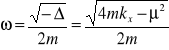
Dla rozwiązania szczególnego otrzymujemy wtedy

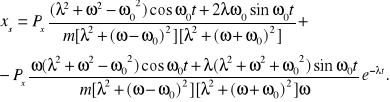
Dla dużych wartości czasu równanie drgań przyjmuje postać

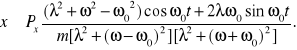
W przypadku braku tłumienia

,

gdzie
.

W przypadku nierezonansowego wymuszenia

oraz

.

w przypadku rezonansu, tzn. gdy
.

Punkt materialny w polu sił centralnych

Załóżmy, że linia działania siły działajacej w dowolnym punkcie pola potencjalnego przechodzi przez stały punkt, zwany środkiem pola. Zatem, jeżeli przyjąć środek pola jako zero układu współrzędnych to w każdym punkcie
pola siła w nim działająca
jest równoległa do
. Wnioskujemy stąd, że w centalnym polu sił moment siły wzgledem środka pola jest zawsze równy zero, a kręt punktu materialnego względem środka pola jest stały względem czasu.

W przypadku prędkości początkowej
równoległej do położenia początkowego
kręt jest zatem zawsze równy zeru i ruch punktu odbywa sie po prostej będącej przedłużeniem
.

W przypadku prędkości początkowej
nierównoległej do położenia początkowego
kręt jest zatem zawsze równy
i ruch punktu odbywa sie w płaszczyźnie prostopadłej do krętu, czyli w płaszczyźnie wyznaczonej przez prędkość początkową
i położenie początkowe
.

W takim przypadku wygodniej jest rozpatrywać ruch punktu w układzie współrzędnych biegunowych
.

Różniczkowanie wzgledem czasu daje następujące wzory na składowe prędkości i przyśpieszenia w prostokątnym układzie współrzędnych

,
,

,

.

Przeliczając je na składowe biegunowe otrzymujemy

,
,

,

.

Z centralności rozpatrywanego pola wynika ponadto, że gradient jego potencjału jest wszędzie skierowany do lub od środka pola, a zatem pole i w konsekwencji siła zależą wyłącznie od odległości od środka pola. Możemy zatem rozważane równania ruchu przedstawić w nastepującej postaci

,
.

Z drugiego równania wynika

gdzie
jest stałą całkowania równą

z warunków początkowych.

Niech

bedzie równaniem toru punktu. Zatem z reguły różniczkowania funkcji złożonej

,

gdzie ' oznacza pochodną względem kąta
. Pierwsze równanie ruchu (
) przyjmuje wtedy postać

którą należy rozumieć jako różniczkowe równanie toru.

Rozwiązanie równania toru zależy od budowy potencjału rozpatrywanego pola sił.

Punkt materialny w polu grawitacyjnym

Załózmy dodatkowo, że siła działająca na punkt jest dana wzorem

gdzie k jest stałą grawitacyjną, a M jest dużą masą wytwarzającą rozpatrywane pole grawitacyjne. Wówczas równanie toru przyjmuje postać

Jest to niejednorodne liniowe równanie różniczkowe drugiego rzędu o stałych współczynnikach. Jego rozwiązanie ma postać

albo równoważnie

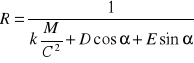
gdzie
i
są stałymi całkowania do wyznaczenia z warunków początkowych. Przyjmijmy układ wspołrzędnych tak aby początkowa wartość kąta
była zerowa. Zatem z warunku początkowej wartości odległości od środka pola znajdujemy

, czyli

Dla wyznaczenia stałej
rozpatrzymy początkową wartość prędkości oddalania się punktu od środka pola

bo

.

Zatem

.

W zależności od warunków początkowych tor może być elipsą, parabolą bądź hiperbolą.

Aby znaleźć równanie ruchu punktu należy rozwiązać równanie

.

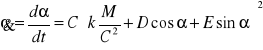
Z twiedzenia o pochodnej funkcji odwrotnej wynika

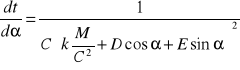
co daje nastepujące wyrażenie na funkcję odwrotną do poszukiwanej

.

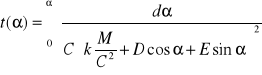
Funkcja odwrotna ma przedstawienie analityczne, niestety zbyt długie do prezentacji w niniejszych materiałach.

Dynamika punktu materialnego z więzami

Więzy są ograniczeniami możliwości poruszania się punktu. Np. dopuszczamy tylko takie równania ruchu punktu
, które spełniają warunek

gdzie
jest równaniem więzu, np. równaniem powierzchni po której porusza się punkt.

Więzy typu
nazywamy dwustronnymi dla odróżnienia od więzów jednostronnych dla których warunek więzu formułujemy w postaci

.

Jeżeli funkcja więzu
nie zależy explicite od czasu to więzy nazywamy stacjonarnymi dla odróżnienia od więzów niestacjonarnych np. dla przypadku punktu poruszającego sie po ruchomej powierzchni.

Wiezy ograniczające położenie nazywamy geometrycznymi.

W prawach dynamiki działanie więzu jest skojarzone z reakcją więzu. Reakcja więzu jest nieznana i należy ją wyznaczyć z praw dynamiki. W przypadku dynamiki punktu materialnego z więzami drugie prawo dynamiki przyjmuje postać

gdzie
jest reakcją więzu w chwili t.

Więzy nazywamy idealnymi, jeżeli dla każdego ruchu zgodnego z warunkiem więzu praca reakcji więzu
jest zerowa. Łatwo można udowodnić, że w przypadku więzu idealnego postaci
, reakcja więzu
musi być równoległa do gradientu fukcji
. Istotnie, różniczkując warunek więzu
po czasie wnioskujemy, że dla dowolnego ruchu zgodnego z więzami prędkość
musi spełniać warunek

czyli musi być prostopadła do gradientu funkcji więzu. Zgodnie z definicją więzu idealnego dla każdego takiego ruchu musi zachodzić
, czyli reakcja musi być prostopadła do prędkości. Skoro tak, to reakcja więzu musi być równoległa do gradientu.

Interpretując równanie więzu jako równanie powierzchni po której purusza się punkt mamy więc konkluzję, że reakcja więzu idealnego jest prostopadła do tej powierzchni.

Punkt poruszający się po powierzchni z tarciem Coulomba

Rozpatrzmy zagadnienie dynamiki punktu poruszającego się po powierzchni danej równaniem

.

Niech
i
oznacza odpowiednio składowe normalną i styczną reakcji więzu. Zatem

;
;

gdzie
jest wartością algebraiczną składowej normalnej reakcji a

jest jednostkowym wektorem normalnym do powierzchni.

Prawo tarcia sformułujemy w postaci

czyli siła tarcia ma kierunek prędkości, zwrot przeciwny, a co do wartości bezwzględnej jest równa
, gdzie
jest współczynnikiem tarcia.

Rozpatrywane zagadnienie sprowadza się więc do rozwiązania następującego układu równań

,
,

z warunkami początkowymi

,
.

Zauważmy, że z warunku więzów wynika

co zróżniczkowane po czasie daje następujące wyrażenie na przyśpieszenie normalne

.

Z drugiej strony rzutowanie drugiej zasady dynamiki na kierunek normalny daje

skąd wynika

Zatem otrzymany układ równań podpada pod przypadek sił zależnych od prędkości.

Dynamika układu punktów materialnych

Rozpatrujemy zagadnienie dynamiki układu wzajemnie oddziałujących N punktów materialnych o masach
. Wprowadzimy następujące oznaczenia

- wektor położenia punktu i w chwili t.

- wektor prędkości punktu i w chwili t.

- wektor przyśpieszenia punktu i w chwili t.

- wektor położenia punktu i względem punktu j w chwili t.

Zakładamy, że w każdej chwili t dowolny punkt j oddziałuje na każdy inny punkt i siłą
spełniającą następujące założenia:

1. Oddziaływania są wzajemne tzn., że
.

2. Oddziaływania są centralne tzn., że wektor
jest równoległy do
.

3. Oddziaływania są potencjalne, tzn., że dla każdej pary punktów i,j istnieje potencjał ich wzajemnego oddziaływania
taki, że

,
,
.

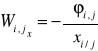
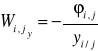
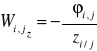
Z założenia wzajemności oddziaływań wynika, że
.

Z założenia centralności wynika, że potencjał oddziaływania punktu j na punkt i zależy tylko od wzajemnej odległości tych punktów, tzn.
i w konsekwencji

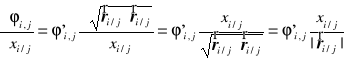
oraz

.

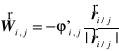
W przypadku szczególnym oddziaływań grawitacyjnych potencjał oddziaływań wyraża się wzorem

.

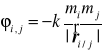
Drugie prawo Newtona dla i-tego punktu materialnego przyjmujemy w postaci

gdzie:
- jest tzw. siłą zewnętrzną działająca na punkt i w danej chwili.

Zasada zachowania pędu układu punktów materialnych

Pędem układu punktów materialnych w danej chwili nazywamy wyrażenie

.

Korzystając z drugiej zasady dynamiki dla układu punktów materialnych obliczamy

.

Wyrażenie
jest sumą wszystkich oddziaływań wewnętrznych układu. Stanowi ono sumę wszystkich pozaprzekątniowych wyrazów macierzy
. Obliczmy tę sumę rozbijając ją na sumę wyrazów powyżej głównej przekątnej liczoną wierszami i sumę wyrazów poniżej głównej przekątnej liczoną kolumnami.

Ale wobec wzajemności oddziaływań mamy

.

Zatem

.

co oznacza, że wektor główny układu sił zewnętrznych działających na rozpatrywany układ punktów materialnych równy prędkości zmian pędu układu.

Zasada zachowania krętu układu punktów materialnych

Krętem (momentem pędu) układu punktów materialnych względem początku układu współrzędnych w danej chwili nazywamy wyrażenie

Korzystając z drugiej zasady dynamiki dla układu punktów materialnych obliczamy

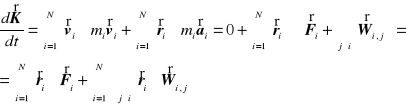
Podobnie do przypadku analizy pędu układu obliczamy sumę
wierszami powyżej głównej przekątnej i kolumnami poniżej otrzymując

.

Wobec wzajemności oddziaływań

oraz ich centralności

.

Ostatecznie

.

co oznacza, że moment główny układu sił zewnętrznych działających na rozpatrywany układ punktów materialnych równy prędkości zmian krętu układu.

Zasada zachowania energii układu punktów materialnych

Energią układu punktów materialnych nazywamy wyrażenie

.

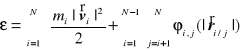
Zauważmy, że wobec symetrii
wyrażenie
- reprezentujące całkowity potencjał oddziaływań wewnętrznych układu - można przedstawić w postaci

.

Obliczając jego pochodną czasową z wykorzystaniem wzajemności oddziaływań otrzymujemy

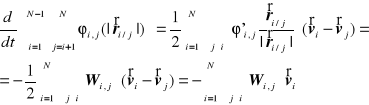
Zatem prędkość zmian energii układu wynosi

co wobec drugiej zasady dynamiki prowadzi do zależności

oznaczającej, że prędkość zmian energii układu punktów materialnych jest równa mocy sił zewnętrznych działających na układ.

Zasada zachowania energii potencjalnej układu punktów materialnych

Jeżeli założyć, że każda z sił zewnętrznych
ma potencjał
, tzn.

,

to można zdefiniować energię potencjalną układu punktów przy pomocy wyrażenia

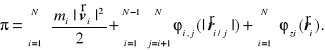
Wtedy otrzymujemy wynik

co oznacza, że w rozpatrywanym przypadku energia potencjalna układu punktów jest stała względem czasu.

Środek masy układu punktów materialnych

Środkiem masy układu punktów materialnych nazywamy punkt
dany wektorem położenia

gdzie
jest łączną masą rozpatrywanego układu. Różniczkując definicję środka masy względem czasu i mnożąc ją przez łączną masę układu otrzymujemy następujący wniosek

co po podstawieniu do zasady zachowania pędu prowadzi do równania

.

Widzimy więc, że pęd układu jest równy pędowi środka masy, a sam środek masy zachowuje się jak zwykły punkt materialny o masie M pod działaniem łącznej siły zewnętrznej.