CZĘŚĆ TEORETYCZNA
1.1 Podstawy teorii płyt.
Płyta jest to dźwigar powierzchniowy , którego grubość jest znacznie mniejsza od pozostałych wymiarów , a ugięcie jest małe w stosunku do grubości . Schematem statycznym płyty jest płaski ustrój dwumiarowy obciążony obciążeniem prostopadłym.
W płytach prostokątnych podpartych na czterech krawędziach uwzględnia się dwukierunkowe zginanie jeśli stosunek długości boków zawiera się w przedziale
0,5 ≤l x/ly≤2,0
Żelbetowe płyty dwukierunkowo zbrojone są powszechnie stosowane w budownictwie m.in. jako stropy budynków , ściany oporowe , ściany zbiorników , płyty fundamentowe itd.
Rodzaje płyt wielokierunkowo zbrojonych .
Płyty wielokierunkowo zbrojone występują w rozwiązaniach konstrukcyjnych jako płyty : podparte wzdłuż całego obwodu , podparte na trzech krawędziach , podparte na dwóch krawędziach , trapezowe i trójkątne o różnych warunkach podparcia , kołowe , pierścieniowe i inne szczególnych kształtów .
Założenia :
płyta wykonana jest z materiału izotropowego , cechującego się liniową sprężystością ;
płyta jest płytą cienką o małych ugięciach .
W miarę wzrostu obciążeń płyty , pierwotnie słusznie założenie izotropii materiału i jego liniowej spężystości odbiega coraz bardziej od rzeczywistości . Powierzchnie płyty się rysują , następuje przegrupowanie sił wewnętrznych zależne teraz nie tylko od warunków brzegowych płyty i jej obciążenia , ale także od rozmieszczenia zbrojenia .
Kształtowanie:
W przypadku płyt prostokątnych podpartych w sposób ciągły wzdłuż obwodu , o ile ![]()
, wymaga się , aby grubość płyty wynosiła co najmniej :
![]()
, dla swobodnego podparcia ,
![]()
, dla sztywnego zamocowania .
Oraz : hp>1/50 lo .
Mniejsze grubości można stosować dla płyt drugorzędnych nie przenoszących żadnych obciążeń poza ciężarem własnym . Przyjęcie grubości jest uwarunkowane osiągnięciem ekonomicznego stopnia uzbrojenia w granicach 0.3 % do 0.9 % .
Modele obliczeniowe płyt w fazie I
Jako model płyty żelbetowej przyjmuje się w fazie sprężystej płytę jednorodną lub anizotropową . Płyta ortotropowa jest dokładniejszym modelem płyty żelbetowej , gdyż umożliwia obliczanie płyt mających różne sztywności w dwóch prostopadłych kierunkach , co pozwala m. in. na uwzględnienie wpływu zbrojenia płyty. Podstawowe założenia obliczeniowe dla płyty sprężystej o małych ugięciach:
płaszczyzna środkowa płyty podczas zginania nie odkształca się i jest powierzchnią oobojętną
proste prostopadłe do płaszczyzny środkowej płyty podczas zginania pozostają prostopadłe do powierzchni środkowej
naprężenia normalne , prostopadłe do powierzchni środkowej płyty mogą być pominięte
Przyjmując powyższe założenia otrzymuje się równanie różniczkowe powierzchni odkształconej oraz wyrażenia umożliwiające obliczenie sił przekrojowych zgodnie z teorią sprężystości . Dla danego schematu płyty możemy otrzymać rozwiązanie ścisłe (met. Naviera, Levy'ego itp.) lub przybliżone (MES , MRS , MEB itp).
Równanie różniczkowe płyty ortotropowej oraz wyrażenia na momenty zginające:
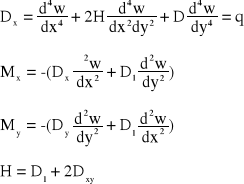
1.3 Modele obliczeniowe płyt żelbetowych w fazie II.
Ponieważ badana płyta była wcześniej zarysowana nie można jej obliczać zgodnie z modelami właściwymi dla fazy I .
W odniesieniu do płyt żelbetowych zarysowanych stosuje się następujące modele obliczeniowe:
model sztywności zastępczej
model lokalnego wpływu zarysowania
Podstawą modelu pierwszego jest uzyskana doświadczalnie uzyskana postać zaawansowanego zarysowania płyty.
Sztywności obliczeniowe płyty określa się w punkcie największych momentów przęsłowych i wykorzystuje rozwiązanie płyty ortotropowej .
Norma PN-84/B-03264 zalecała obliczanie ugięć płyt krzyżowo zbrojonych zgodnie ze wzorami teorii izotropowych płyt sprężystych . Za sztywność w tym przypadku należało przyjmować dla fazy II :
D=1,1BII
gdzie zgodnie z PN-99/B-03264
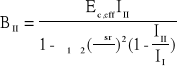
Drugi model obliczeniowy umożliwia dokładniejszą analizę różnych stanów zarysowania płyty ( rys 2) , ale jest modelem bardzo złożonym matematycznie.
Uwaga : Szczególną uwagę zwrócić należy na pracę naroża swobodnie podpartego. Jeżeli bowiem obciążymy płytę swobodnie podpartą to jej naroża mają tendencję do uniesienia się . W rzeczywistości obciążenia działające na krawędż płyty oraz połączenia konstrukcyjne uniemożliwiają w przeważającej liczbie przypadków uniesienie naroży . Efektem tego działania jest pojawienie się w narożu oddziaływania które dociska płytę do podpory . To skoncentrowane oddziaływanie powoduje powstanie w narożu momentów zginających , mogących doprowadzić do jego zarysowania . Dlatego też we wszystkich przypadkach swobodnie podpartych płyt , w których uniemożliwione jest uniesienie naroży , stosuje się dodatkowe ich zbrojenie.
W przypadku naroża płyty o krawędziach zamocowanych wartości momentów zginających zanikają ku narożu .
OPIS BADAŃ
Element badany.
Elementem badanym był model kwadratowe płyty żelbetowej krzyżowo zbrojonej swobodnie poddpartej na wszystkich krawędziach , wykonany w skali 1:3 . Geometia elementu , układ sił obciążających oraz układ czujników był zgodny z rys.3
Cel badań , program obciążeń.
Celem badań było porównanie wyznaczonych teoretycznie i doświadczalnie sztywności oraz przemieszczeń w żelbetowej płycie dwukierunkowo zbrojonej obciążonej statycznie.
Program obciążenia i odciążenia elementu badanego został zamieszczony w tabeli pomiarów ugięć i zarysowań. Program obciążania i odciążania płyty został przeprowadzony jednokrotnie. W czasie badań nie prowadzono pomiaru szerokości rozwarcia rys.
Opis stanowiska badawczego.
Stanowisko badawcze stanowi urządzenie dżwigniowo balastowe składające się z poziomej ramy (podpora płyty),ramy portalowej służącej realizacji obciążenia oraz dźwigni dwustronnej. Balast powoduje , że badana płyta poprzez system lin i trawersów jest podciągana ku górze . Odkształcając się powoduje wciskanie trzpieni czujników zegarowych zamocowanych przy pomocy prętów do górnej krawędzi ramy poziomej,co pozwala na rejstrację zmian ugięć płyty wraz ze zmianami obciążeń (zmiany obciążeń rejstróje dynamometr wmontowany w jedno z cięgien.
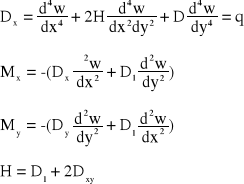
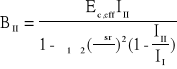
Wyszukiwarka
Podobne podstrony:
laborBet, Prywatne, Budownictwo, Materiały, IV semestr, IV sem, Konstrukcje betonowe, BETON laborki
Cwiczenia1 konstrukcje betonowe
zelbet test, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje Betonowe II, egza
Projekt 1 Konstrukcje Betonowe
Pn 88 B 01041 Rysunek Konstrukcyjny Budowlany Konstrukcje Betonowe,Żelbetowe I Sprężone
Konstrukcje betonowe podstawy zaliczenie wykładu (D S )
notatek pl konstrukcje betonowe 1 pytania egzaminacyjne 10
452 2 KONSTRUKCJE BETONOWE
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c2
Konstrukcje betonowe Wymiarowanie słupa
Złożone konstrukcje betonowe II
notatek pl konstrukcje betonowe 1 pytania egzaminacyjne 9
str. na teczkę, STUDIA, Budownictwo UZ, Semestr IV, Konstrukcje Betonowe - Podstawy [Korentz], Labol
Żelbet - Egzamin - Zagadnienia, Budownictwo S1, Semestr IV, Konstrukcje betonowe, Egzamin
więcej podobnych podstron