ZASADA PAULIEGO

• Układ okresowy pierwiastków lub jakiekolwiek zestawienie danych fizyko-chemicznych pokazuje, ze właściwości tych pierwiastków powtarzają się cyklicznie w grupach 2, 8, 8, 18, 18, 32... -elementowych.

• Wolfgang Pauli (1900-1958) podał w 1925 roku zasadę (zwana też zakazem Pauliego), która „generuje” takie właśnie liczebności grup:

- na jednej orbicie mogą znajdować się nie więcej niż dwa elektrony, opisane tą samą falą stojącą (funkcją falową).

ZASADA PAULIEGO - c.d.

• Zasada Pauliego była wprowadzona empirycznie (bez dowodu ani uzasadnienia), ale dobrze wyjaśniała opisywaną liczebność grup (razem z istniejącą już kwantową teorią atomu i pojęciem liczb kwantowych):

• dla
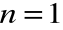
  (główna liczna kwantowa) mamy jedną możliwość: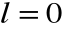
  i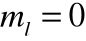
  - czyli dwa elektrony;

• dla
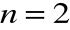
  może być już: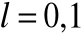
  i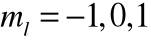
  , co daje dokładnie cztery kombinacji: (2,0,0), (2,1,-1), (2,1,0) i (2,1,2) a więc zgodnie z zasadą Pauliego osiem elektronów;

• dla
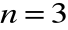
  dochodzi pięć nowych kombinacji: (3,2,-2), (3,2,-1), (3,2,0), (3,2,1) i (3,2,2) co daje w sumie dziewięć kombinacji i osiemnaście funkcji elektronowych.

SPIN ELEKTRONU

• Zaledwie rok później odkryto, że wszystkie elektrony mają wewnętrzny (a więc nie związany z ruchem o orbicie wokół atomu) moment pędu równy:

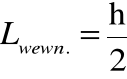
który nazwany został spinowym momentem pędu.

• Elektron zachowuje się więc jakby był wirującą kulką o ustalonym momencie pędu, równym połowie naturalnej jednostki momentu pędu
! Ten wewnętrzny moment pędu nie zwiększa się ani nie maleje.

Później okazało się również, że istnieją inne cząstki elementarne, których spin też równy jest
.

• P.M. Dirac i W. Pauli stworzyli po odkryciu spinu elektronu relatywistyczną teorię kwantową dla cząstek o spinie ½ i stwierdzili, że z warunków niezmienniczości wynikają funkcje falowe elektronów, które spełniają zasadę Pauliego - cząstka o takim spinie może mieć składowe momentu pędu wzdłuż osi
tylko równe
lub
- do opisu funkcji falowej elektronu doszła jeszcze jedna liczna kwantowa.

ATOMY WIELOELEKTRONOWE

• Równanie Schrödingera i zasada Pauliego stanowią podstawy teorii, dzięki której możemy przewidzieć właściwości pierwiastków bez przeprowadzania doświadczeń chemicznych!

• W praktyce często łatwiej jednak wykonać doświadczenie niż przeprowadzać żmudne i czasochłonne obliczenia komputerowe...

• Dla wodoru (liczba atomowa
) zgodnie z teorią jedyny elektron może przyjąć energię stanu kwantowego
, którego energia wynosi
- taka energia jest potrzebna by atom zjonizować, czyli wyrwać z niego ten jedyny elektron.

• Potencjał, odpowiadający wielkości energii, potrzebnej do zjonizowania atomu, nazywamy potencjałem jonizacji.

ATOMY WIELOELEKTRONOWE - c.d.¹

• W atomie helu (
), który ma dwa elektrony, również jądro ma ładunek
. Orbity elektronowe mają ten sam kształt, ale stałą proporcjonalności należy pomnożyć przez
.

• atom helu z jednym elektronem (jednokrotnie zjonizowany) będzie więc miał energię jonizacji:

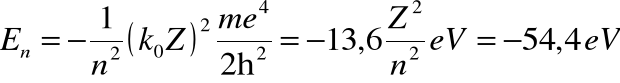
Tyle trzeba dostarczyć energii, żeby oderwać drugi elektron ze zjonizowanego atomu!

• drugi elektron będzie najpierw „widział” obiekt o ładunku
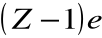
  a dopiero po dostaniu się na powłokę
  „zobaczy” cały ładunek jądra
  - możemy więc założyć, że efektywny ładunek jądra, jaki „czują” elektrony w atomie helu jest średnią: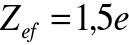
  . Możemy więc uogólnić zależność na energię jonizacji:

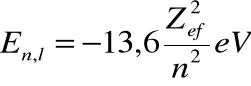
gdzie
zależy od obu liczb kwantowych
i
.

Z takiego szacowania otrzymujemy dla helu potencjał jonizacji (pierwszego elektronu) rzędu
. Dokładniejszy model daje wartość bardziej zbliżoną do wartości doświadczalnej:
.

ATOMY WIELOELEKTRONOWE - c.d.²

• W przypadku litu (
), zgodnie z zasadą Pauliego, dwa elektrony obsadzą pierwszy orbital (powłokę)
a trzeci elektron musi znaleźć się już na orbitalu o głównej liczbie kwantowej
.

• podwójnie zjonizowany atom litu zachowuje się jak atom wodoropodobny (jeden elektron „krążący” wokół jądra) ale energię jonizacji trzeba pomnożyć przez czynnik
  ;

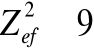
• jednokrotnie zjonizowany atom litu ma widmo podobne do widma atomu helu, ale
  ;

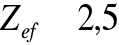
• trzeci elektron, znajdujący się na powłoce o wyższej energii (a więc również i większej średniej „odległości” od jądra) „widzi” efektywny ładunek jądra i dwóch poprzednich elektronów nieco większy od
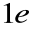
  . Doświadczalnie wyznaczony potencjał jonizacji tego elektronu jest równy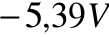
  , co odpowiada ok.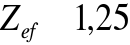
  .

Aby dostać podwójnie zjonizowany atom litu, należałoby jeszcze oderwać drugi elektron, co wymagałaby potencjału ok.
- dlatego atom litu można w praktyce zjonizować tylko jednokrotnie.

ATOMY WIELOELEKTRONOWE - c.d.³

• Potencjał efektywny
zależy od obu liczb kwantowych,
i
co w praktyce powoduje, że dla atomów wieloelektronowych energia stanu o niższej liczbie głównej
ale wysokiej liczbie
może być większa, niż energia stanu o nieco wyższej (
) głównej liczbie kwantowej, ale małej liczbie
(odpowiadającej za moment pędu elektronu na danej orbicie).

Przykład:

Dla potasu (
) poziom (
,
) leży niżej (tzn. ma niższą energię efektywną) niż poziom (
,
). O tym potem...

• Interpretacja: kształt orbity o większym momencie pędu jest bardziej zbliżony do okręgu (sfery), co pociąga za sobą większą średnią odległość elektronu od jądra niż dla orbity o mniejszym momencie pędu (mniejszej liczbie kwantowej
). Dlatego stany o niższej orbitalnej licznie kwantowej
są stanami silniej związanymi.

ATOMY WIELOELEKTRONOWE - c.d.⁴

• Beryl (
ma dwa elektrony (silnie związane, co już zrozumiałe) na pierwszej powłoce (
), ale też dwa elektrony na drugiej (
,
).

• pierwszy potencjał jonizacji jest większy niż dla atomu litu, bo ładunek efektywny
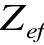
  dla tej części funkcji falowej elektronu, która przebiega bliżej jądra, jest większy; wynosi on ok.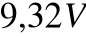
  ;

• drugi potencjał jonizacji nie jest jednak dużo większy, bo drugi elektron znajduje się w stanie
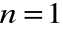
  i „czuje” potencjał efektywny niewiele większy, niż pierwszy elektron;

• następne dwa potencjały jonizacji są bardzo duże, bo dwa „wewnętrzne” elektrony „widzą” dużo większy ładunek jądra.

Ze względu na to, że oba potencjały są tego samego rzędu, beryl wykazuje w związkach chemicznych wartościowość
(energia reakcji chemicznej „wystarczy” na podwójną jonizację).

ATOMY WIELOELEKTRONOWE - c.d.⁵

• Bor (
), węgiel (
), azot (
), tlen (
), fluor (
) i neon (
).

• Zapełniane są kolejno stany
powłoki
. Ponieważ dla
możliwe są trzy różne wartości
(poboczna liczba kwantowa), podpowłoka ta może „przyjąć” sześć elektronów.

• Podobna do poprzednio przeprowadzonej analiza przekonuje, że stosunkowo łatwo można zjonizować odpowiednio 3 (dla boru) 4 (dla węgla) i 5 (dla azotu) elektrony (dwa z poprzedniej podpowłoki
i pozostałe z tej o
).

• Proces zwany hybrydyzacją powoduje zresztą, że wszystkie 3 atomy dla boru i 4 dla węgla grają podobną rolę w procesie tworzenia związku chemicznego).

• Dla atomu azotu okazuje się, że energia jonizacji wszystkich pięciu elektronów tej podpowłoki jest porównywalna z energią, potrzebną do przyłączenia trzech atomów (więcej nie można w myśl zakazu Pauliego!)...

ATOMY WIELOELEKTRONOWE - c.d.⁵

• W przypadku tlenu i fluoru występuje nowe zjawisko, zwane powinowactwem elektronowym - zdecydowanie mniejszej energii potrzeba do przyłączenia kolejnych elektronów (jednego dla fluoru, dwóch dla tlenu) niż zjonizowanie wszystkich z całej podpowłoki.

Np. dla fluoru energia wiązania tego dodatkowego elektronu to tylko
. Dla tlenu energia wiązania pojedynczego „dołączonego” elektronu wynosi ok.
.

• W neonie wszystkie stany powłoki
są zapełnione - nie da się dołączyć już żadnego elektronu (dołączenie na wyższą, do tej pory ”gołą”, powłokę wymaga wielkiej energii) a jonizacja takiej „pełnej” powłoki też byłaby duża (ok.
), więc neon jest równie nieaktywny chemicznie jak hel.

• Od sodu (
) do argonu (
) sytuacja się powtarza:
,
równe najpierw
(dwa elektrony), potem
(sześć elektronów, bo teraz jeszcze
), podobne zasady obsadzania podpowłok i wartości energii jonizacji.

ATOMY WIELOELEKTRONOWE - c.d.⁶

• Jak już wspomniano, potencjał efektywny
zależy od obu liczb kwantowych
i
co powoduje w szczególności, że dla wyższych liczb orbitalnych
może się zdarzyć, że potencjały te są „przestawione” w szeregu wartości. Dla potasu (
) jest właśnie tak, że potencjał efektywny podpoziomu (
,
) jest większy niż potencjał dla podpoziomu (
,
), co daje w wyniku mniejszą energię wiązania elektronu na podpowłoce (
,
)! Powoduje to, że w potasie ( i następnym wapniu) najpierw zapełniana jest (dwa kolejne elektrony) podpowłoka (
,
), a dopiero potem (
,
).

• Począwszy od skandu (
) nastąpi teraz obsadzanie kolejnych dziesięciu stanów podpoziomu (
,
) (dziesięć elektronów, jako że teraz
) a później sześciu stanów podpoziomu (
,
). Całkowita liczba stanów elektronowych o zbliżonych energiach jest więc równa:

i stąd bierze się liczba 18 w szeregu własności atomów.

ATOMY WIELOELEKTRONOWE - c.d.⁷

• Można w ten sposób wyznaczyć kolejne potencjały jonizacji i poziomy energetyczne a także powinowactwa elektronowe atomów za pomocą komputera. I choć wymaga to olbrzymiej ilości obliczeń - całą chemię można wyjaśnić za pomocą mechaniki kwantowej elektronu o spinie ½!

• Należy zwrócić uwagę na szczególnie duże przerwy energetyczne następujące po zapełnieniu powłok 2, 10, 18, 36, 54 i 86-ma elektronami - elektrony są wtedy mocno związane i pierwiastki o takich konfiguracjach są mało aktywne chemicznie.

PROMIENIE X

• Dla atomów o dużej liczbie atomowej
energie wiązań zewnętrznych elektronów są niewielkie (mniejszy jest ładunek efektywny
„widziany” przez te elektrony ze względu na „ekranowanie” przez elektrony z niższych powłok, zwłaszcza te o
). Ale za to energie wiązań dwóch pierwszych elektronów na powłoce
są olbrzymie, rzędu
!

• Gdyby udało się jednak „wyrwać” taki elektron z powłoki, ewentualnemu spadkowi elektronu z zewnętrznej powłoki na zwolnione miejsce towarzyszyłaby emisja wysokoenergetycznego fotonu o długości fali rzędu pojedynczych angstremów (Å). Dokonuje się tego poprzez bombardowanie atomów strumieniem elektronów o energiach rzędu
.

• Takie promieniowanie elektronów powłoki K (wewnętrznej) nazywane jest promieniowaniem X i używane jest (ze względu na długość fali porównywalną z rozmiarami atomów) do badań struktury atomowej pierwiastków.

WIĄZANIA CZĄSTECZEK

• Opisano dotąd strukturę elektronową pojedynczych atomów. W przypadku cząsteczek struktury te są bardziej skomplikowane i można je wyjaśnić opisując zachowanie elektronów składowych atomów cząsteczki w polu ich wspólnego potencjału.

• W zależności od zachowania elektronów na ostatnich powłokach składowych atomów cząsteczki, możemy wyróżnić dwa rodzaje wiązań atomowych: jonowe i kowalencyjne.

• Wiązanie jonowe: zewnętrzny elektron jednego atomu, słabiej z nim związany niż odpowiednie elektrony ostatniej powłoki drugiego atomu, zostaje przez ten drugi atom „przywłaszczony”; tworzą się w ten sposób dwa jony oddziaływujące ze sobą elektrostatycznie, co daje trwałe wiązanie między tymi atomami;

Przykład: cząsteczka fluorku litu (LiF):

- Energia jonizacji litu równa jest 5,4 eV.

- Powinowactwo elektronowe fluoru równe jest 3,6 eV.

- Wypadkowa energia potrzebna do oderwania elektronu od atomu litu: 1,8 eV.

- Energia elektrostatyczna jest równa 1,8 eV dla odległości między atomami równej 8 Å - wtedy elektron „przeskakuje” z atomu litu do fluoru.

WIĄZANIA CZĄSTECZEK

• Wiązania kowalencyjne: (rozpowszechnione w cząsteczkach organicznych) polegają na „uwspólnieniu” elektronów z zewnętrznych powłok przez oba atomy, wiążące się ze sobą.

Wiązania kowalencyjne występują wtedy, gdy mamy do czynienia z pewną „symetrią” zagadnienia: łączą się dwa atomy tego samego pierwiastka (
,
) albo cząstka ma środek symetrii (metan
). Odpowiednia funkcja falowa, opisująca takie „wspólne” elektrony daje wtedy mniejsze wartości energii.

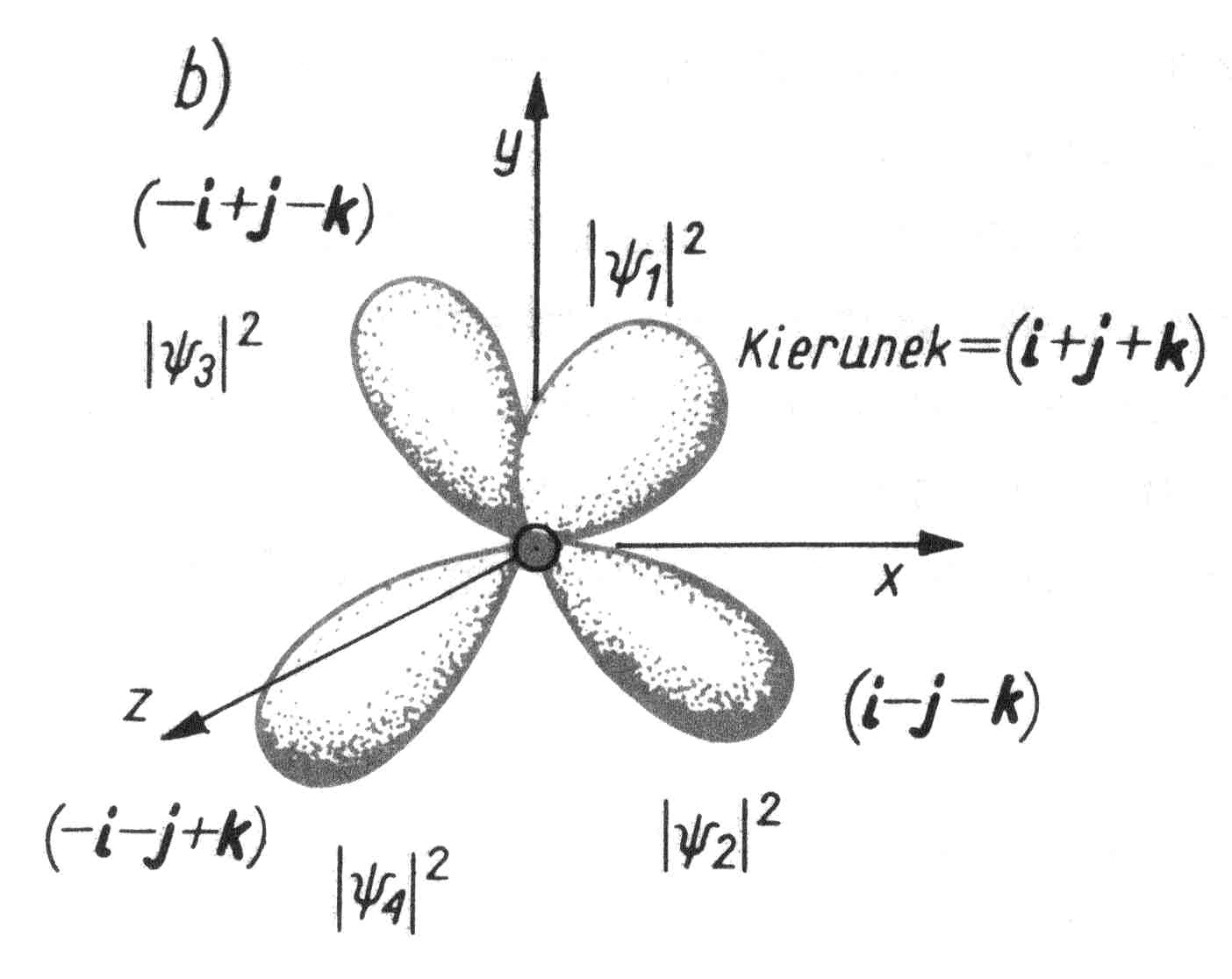
HYBRYDYZACJA

• W swobodnym atomie znajdują się na innych podpowłokach a więc mają inne energie, są inaczej związane z atomem (np. elektrony w stanie
są silniej związane niż te z podpowłoki
).

• W trakcie tworzenia cząsteczek atomy z poszczególnych podpowłok ostatniej powłoki traktowane są jednak równoważnie - jak pokazał przykład wiązania kowalencyjnego między atomem węgla (na powłoce
są dwa elektrony z
i dwa z
). Jest to wynikiem tego, że atomy wchodzące w skład cząsteczki nie są takie same, jak atomy izolowane.

• Rozwiązanie równania Schrödingera dla układu kilku jąder atomowych (skomplikowana funkcja, opisująca potencjał) nie jest łatwe, ale możliwe... Efekt zaprezentujmy na przykładzie omawianej cząstki metanu (
).

HYBRYDYZACJA - c.d.¹

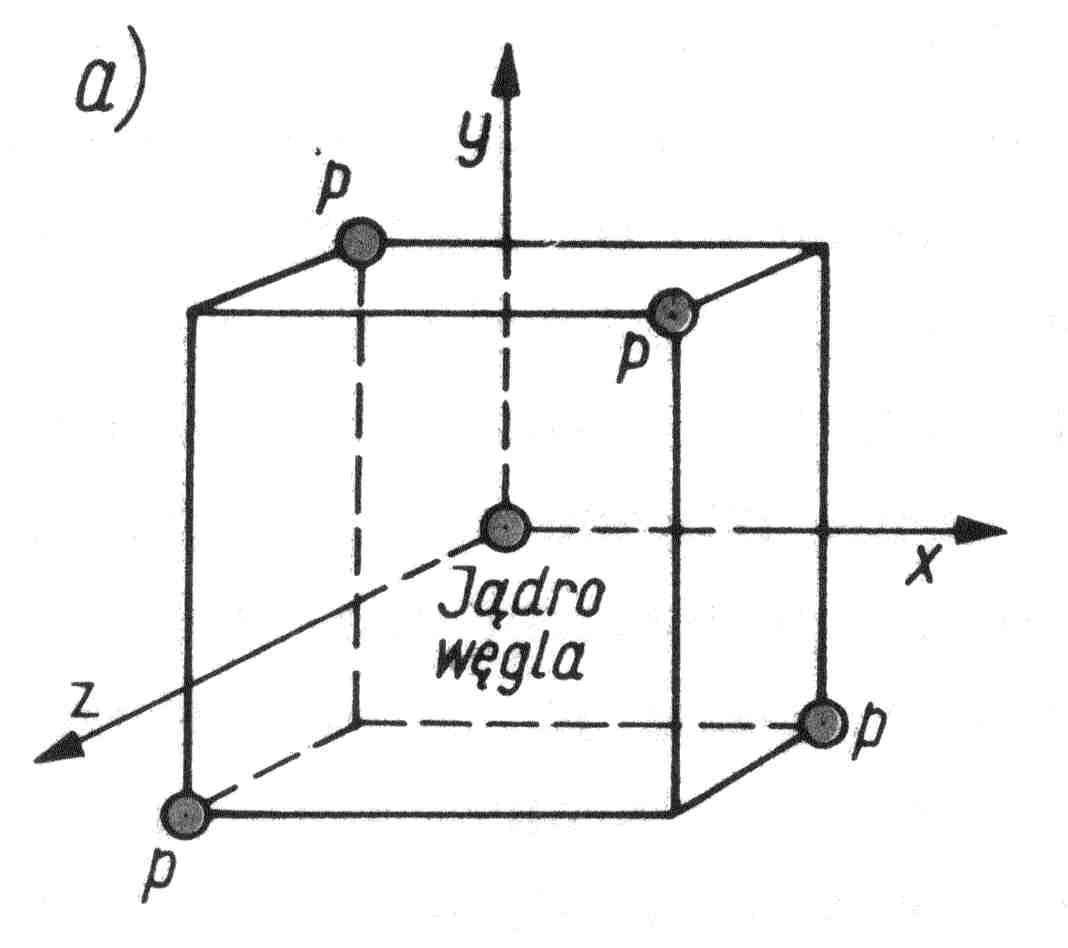
• Fale stojące, opisujące cztery zewnętrzne elektrony atomu węgla w takiej cząstce metanu, znacznie różnią się od rozwiązań dla atomu swobodnego, ale można je przedstawić w postaci sumy (kombinacji liniowej) funkcji atomu wodoropodobnego! Energie wiązania czterech zewnętrznych elektronów są jednakowe i równają się energii wiązania elektronu w stanie
.

• Rzeczywiście, funkcje falowe tych elektronów można zapisać jako superpozycje funkcji falowych elektronów atomu wodoropodobnego:

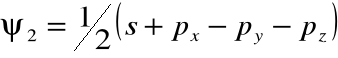
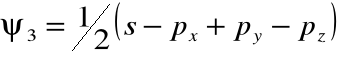
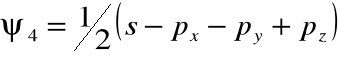
gdzie:

;
;

;
;

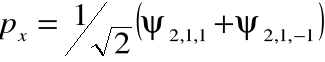
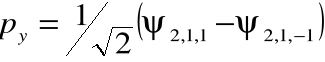
HYBRYDYZACJA - c.d.²

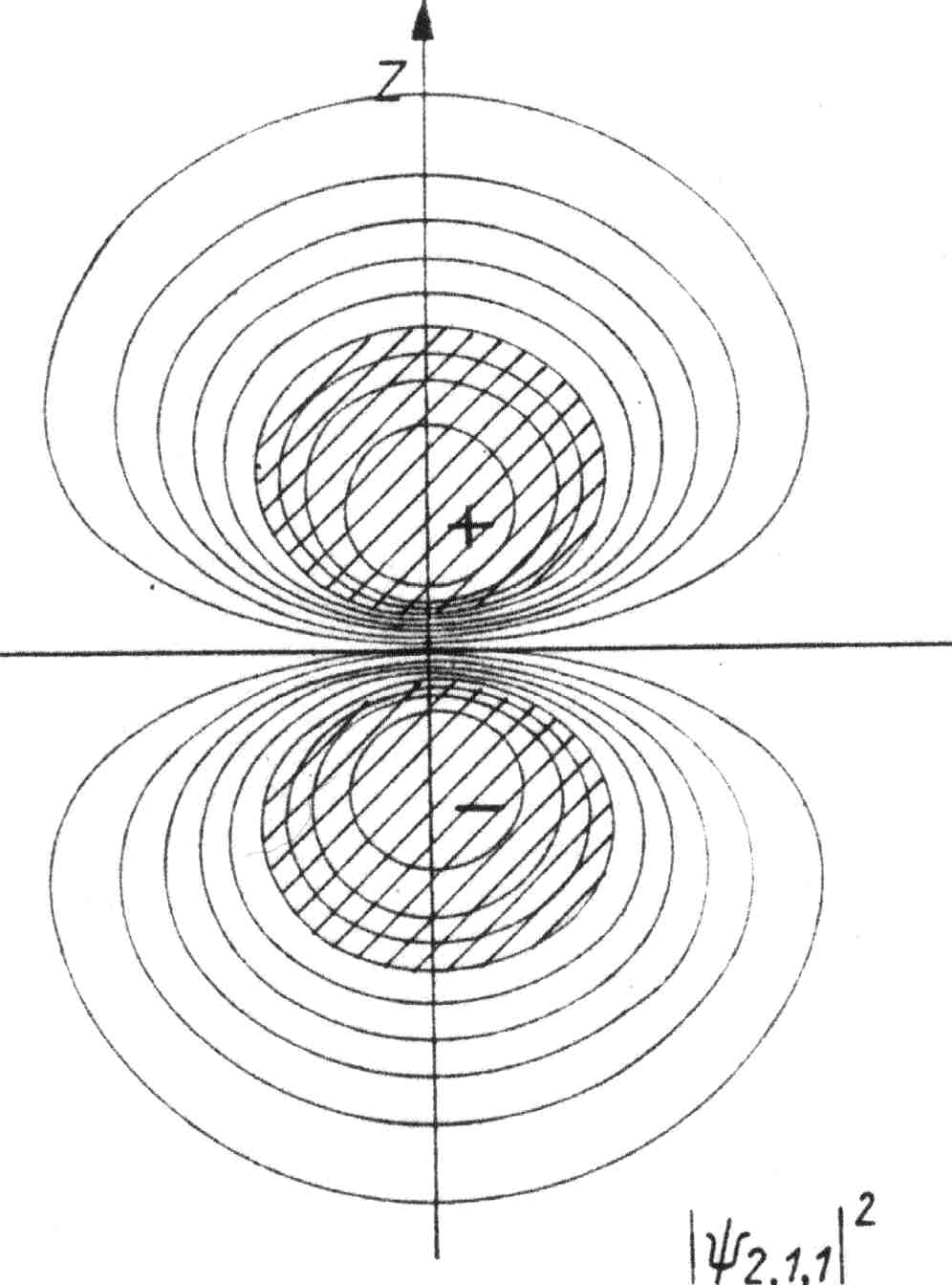
• Tak utworzone funkcje falowe są mocno niesymetryczne, „rozciągnięte” w jednym kierunku (np. osi
).

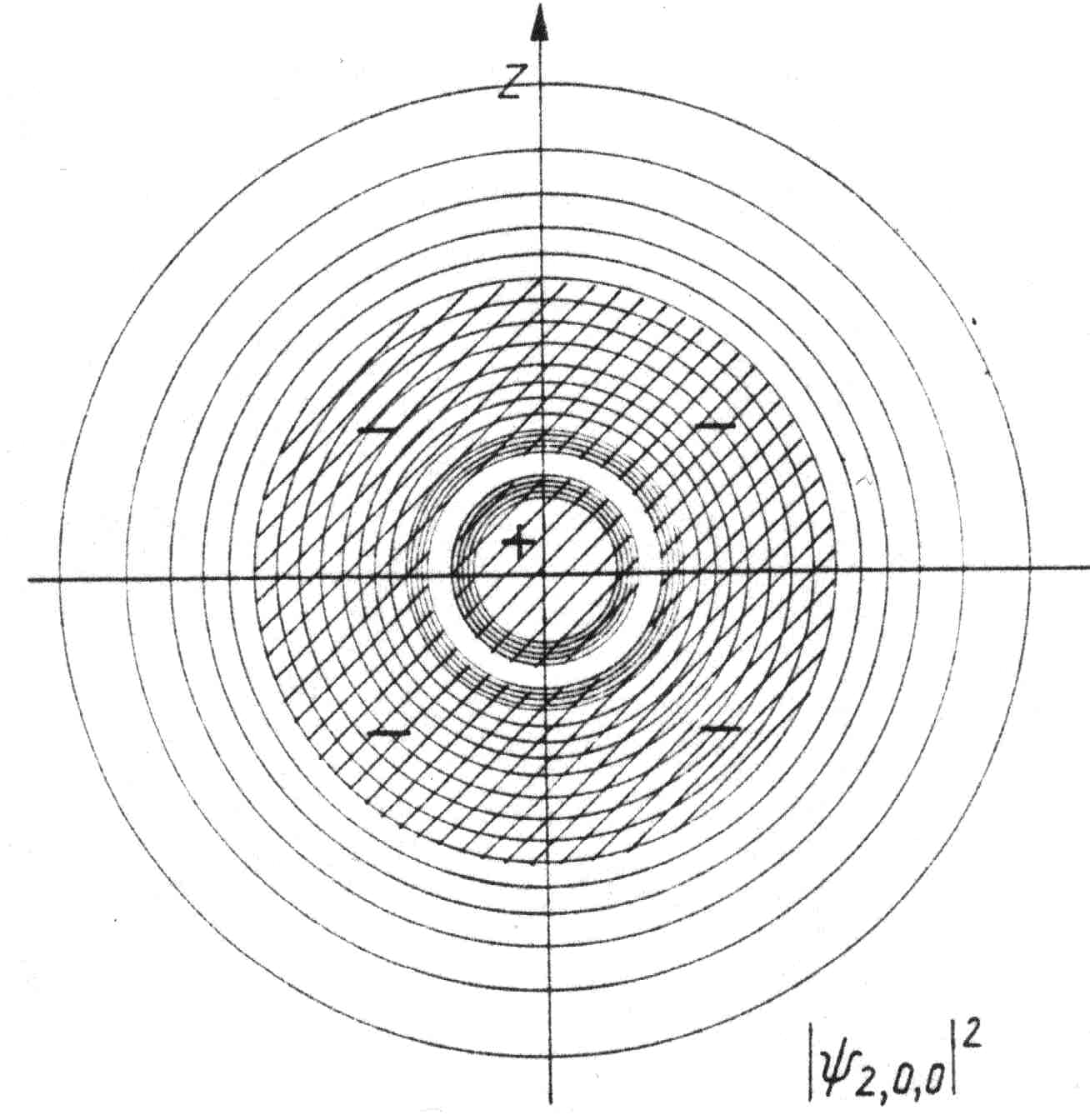
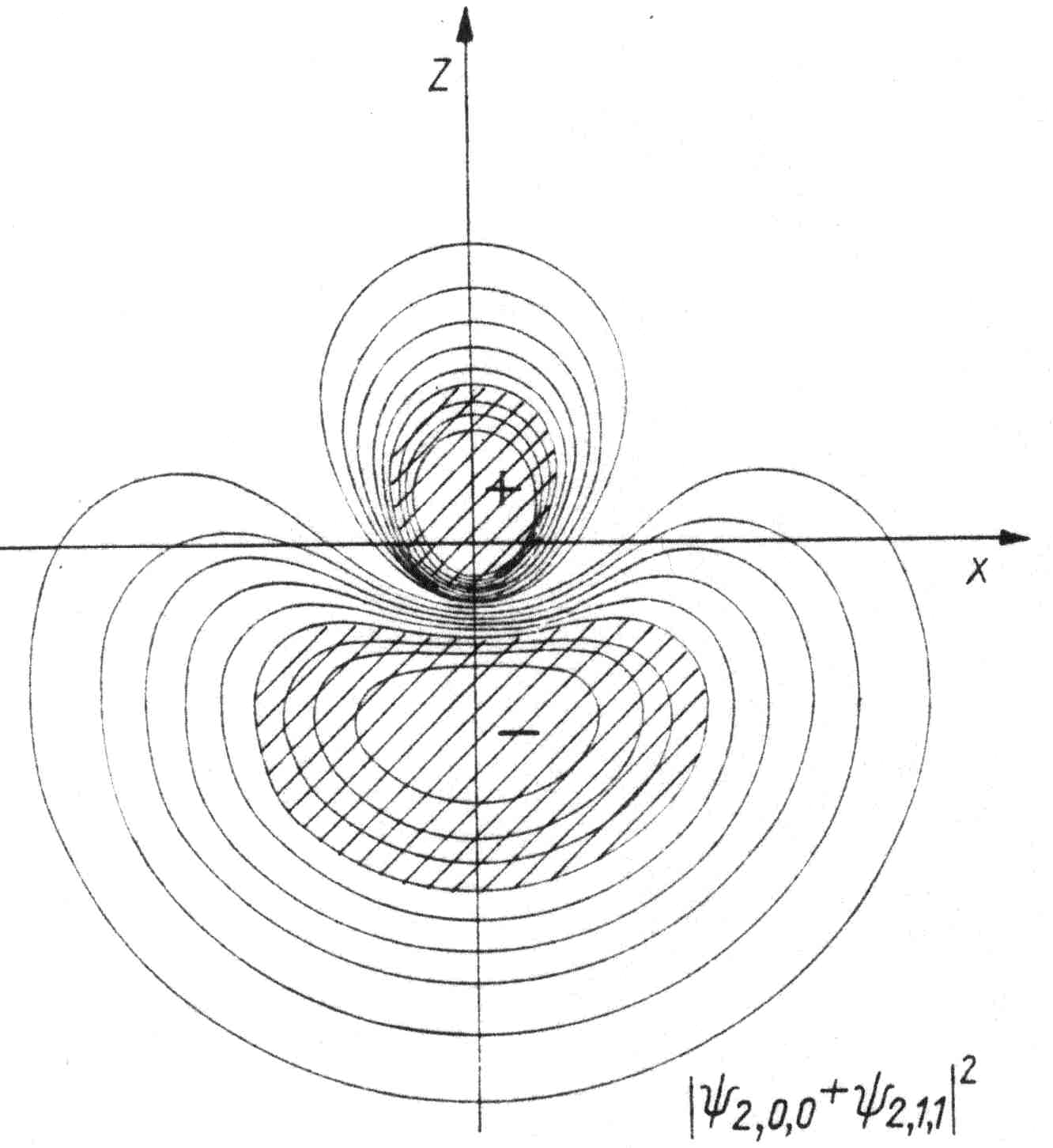
• Taka procedura dodawania funkcji falowych izolowanych atomów, by tworzyły one „płaty” rozciągające się w określonych kierunkach, jest nazywana hybrydyzacją. „Chmura” elektronowa, opisana jako taka kombinacja, nazywana jest hybrydą
.

16

---