Macierze i wyznaczniki.

Macierzą prostokątną o „m” wierszach i „n” kolumnach nazywamy układ m*n elementów
jednoznacznie przyporządkowanych parom wskaźników

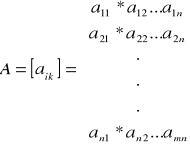
Gdy m=n macierz nazywamy macierzą kwadratową, gdzie „n” jest stopniem macierzy.

Linia
nazywa się przekontną główną macierzy, natomiast suma
nazywa się śladem macierzy.

Jeżeli elementy na głównej przekątnej macierzy są równe 1, a pozostałe elementy są równe 0 to macierz nazywamy macierzą jednostkową.

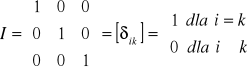
(i)

symbol Kroneckera

- grecka delta.

Macierz diagonalna, gdy zamiast jedynek na przekątnej są inne liczby.

1. Dodawanie macierzy.
   
   
   
   
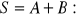
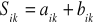
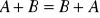
   - przemienność dodawania.

2. Mnożenie macierzy przez liczbę.
   
   
   

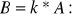
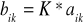
3. Mnożenie macierzy przez macierz.
   Mnożenie macierzy jest wykonalne jeżeli liczba kolumn macierzy pierwszej jest równa liczbie wierszy macierzy drugiej.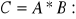
   
   
   
   
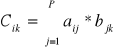
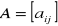
   macierz typu (m, p)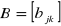
   
   macierz typu (p, n)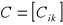
   
   macierz typu (m, n)
   !!
   !! MNOŻENIE NIE JEST PRZEMIENNE.

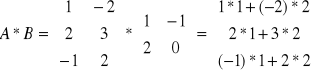
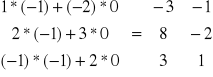
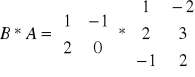
NIE DA SIĘ POMNOŻYĆ.

Pojęcie macierzy transporowanej (przestawiona).

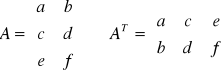
Macierz kwadratowa symetryczna.
.

jest to macierz, która równa jest macierzy transporowanej.

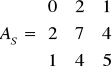
Macierz antysymetryczna (skośnie symetryczna).
.

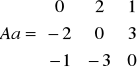
Twierdzenie.

Każdą macież kwadratową można przedstawić jako sumę macierzy symetrycznej i antysymetrycznej.

Każdej macierzy kwadratowej można przypisać wyznacznik, a wyznacznikowi liczbę zwaną wartością wyznacznika.

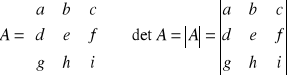
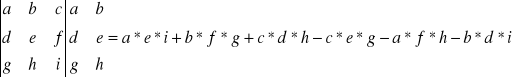
Minorem
elementu
wyznacznika
macierzy kwadratowej A stopnia „n” nazywamy wyznacznik stopnia o 1 mniejszego, powstający przez usunięcie wiersza i kolumny, który znajduje się element
.

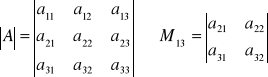
Dopełnieniem algebraicznym
elementu
jest iloczyn tego minora i czynnika
.

Definicja wyznacznika według Laplace'a:

Wyznacznik jest równy sumie iloczynów elementów dowolnego wiersza lub kolumny i ich dopełnień algebraicznych.

Rozwiązywanie układów równań liniowych.

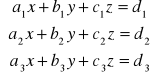
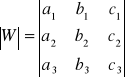
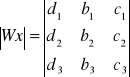
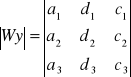
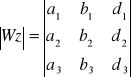
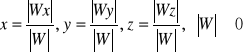
1. Układ jest oznaczony
   

2. Układ jest nieoznaczony
   

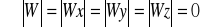
3. Układ jest sprzeczny
   

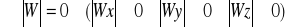
Obliczanie macierzy odwrotnej. !!

Macierz nazywamy macierzą nieosobliwą, gdy jej wyznacznik jest różny od zera.

Dla macierzy nieosobliwej
można obliczyć macierz odwrotną.

Oblicz macierz odwrotną do macierzy:

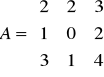
1. Obliczamy wyznacznik macierzy A. !!
   
   

2. 
   
   
   
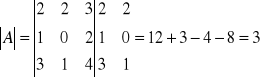
   Macierz minorów.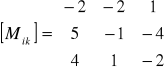
   
   najlepszy - zostawiamy
   

3. Macierz dopełnień algebraicznych.
   
   

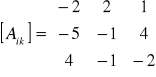
4. Macierz dołączona.
   
   

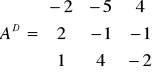
5. Macierz odwrotna.
   
   

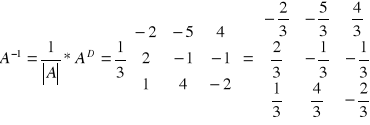
6. Sprawdzenie.
   
   

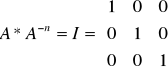
Rząd macierzy (rank A):

1. Macierz zerowa ma rząd równy zero.

2. Jeżeli nie wszystkie elementy macierzy są równe zero, ale wszystkie wyjęte z macierzy wyznaczniki stopnia drugiego lub wyższego są równe zero to macierz jest rzędu pierwszego.

3. Jeżeli wszystkie wyznaczniki stopnia wyższego od r są równe zero, a przynajmniej jeden wyznacznik stopnia
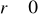
   to macierz jest r.

Twierdzenie Kroneckera-Capellego:

Układ równań ma rozwiązanie, jeżeli rząd macierzy współczynników i rząd macierzy uzupełnionej U są równe.

Jeżeli wspólny rząd macierzy współczynników i macierzy uzupełnionej „r” jest równy liczbie niewiadomych „n”, to istnieje dokładnie jedno rozwiązanie.

Jeśeli r<n to istnieje nieskończenie wiele rozwiązań zależnych od (n-r) - parametrów.

Rozwiązanie układu równań.

1. 
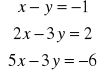
   Określamy rząd macierzy współczynników.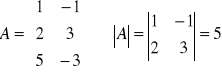
   
   rank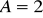
   

2. Tworzymy macierz uzupełnioną U i obliczamy jej wyznacznik.
   
   
   
   
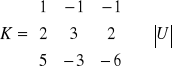
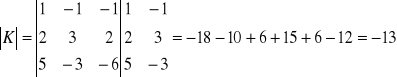
   rank U = 3
   Ponieważ rank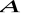
   rank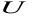
   z twierdzenia Kroneckera-Capellego, układ nie ma rozwiązania.

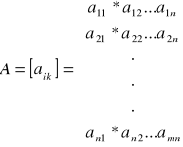
A*B

---