Temat: Równowaga względna cieczy.

1. Cel ćwiczenia
   Celem ćwiczenia jest zaobserwowanie zachowania się cieczy w naczyniu cylindrycznym, wirującym wokół osi pionowej oraz doświadczalne i teoretyczne wyznaczenie kształtu swobodnej powierzchni cieczy

2. Podstawy teoretyczne

Stan względnego spoczynku zachodzi wtedy, gdy ciecz wraz z naczyniem znajduje się w ruchu ze stałą prędkością, bądź ze stałym przyspieszeniem, tzn. wtedy, gdy cząstki cieczy nie przemieszczają się względem siebie ani naczynia.

Stan względnego spoczynku cieczy opisuje układ równań różniczkowych Eulera:

Mnożąc te równania odpowiednio przez dx, dy, dz i dodając stronami otrzymujemy:

Gdzie:

- gęstość cieczy

X, Y, Z - składowe jednostkowej siły masowej

dp- różniczka zupełna funkcji ciśnienia p=p(x,y,z)

Siły masowe, a wiec siły związane z masą ciała, które działają na każdą cząstkę są proporcjonalne do masy cieczy. W rozważanym przypadku w jej skład wchodzi siła ciężkości oraz siła odśrodkowa. Występują jeszcze siły oddziaływań grawitacyjnych z innymi planetami układu Słonecznego i nie tylko, księżycem oraz siła Coriolisa spowodowana ruchem obrotowym ziemi.

Równanie (2) jest podstawowym równaniem równowagi cieczy w stanie względnego spoczynku i podaje związek między ciśnieniem dowolnym punkcie cieczy a siła, jaka działa na ciecz w tym punkcie.

Powierzchnia swobodna cieczy jest powierzchnią izobaryczną, tzn. powierzchnią jednakowego ciśnienia, na której p=p(x,y,z)=constans czyli dp=0. Uwzględniając ten fakt , z równania otrzymujemy:

W naczyniu cylindrycznym, poruszającym się ruchem jednostajnie obrotowym wokół pionowej osi powierzchnia swobodna ma kształt paraboloidy obrotowej o osi pokrywającej się z osia obrotu naczynia. Kształt tej powierzchni można opisać teoretycznie wychodząc z równania równowagi płynu. Na dowolny element płynu, znajdujący się w punkcie M9x,y,z) działa jednostkowa siła masowa o składowych:

Gdzie:
- prędkość kątowa ruchu naczynia 1/s

n - prędkość obrotowa 1/min

Podstawiając do równania otrzymujemy:

Nastepnie całkując jako całke iterowaną otrzymujemy:

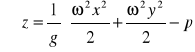
Wprowadzając współrzędne walcowe możemy równanie przekształcić do postaci:

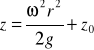
Co jest równaniem paraboloidy obrotowej opisującym swobodną powierzchnię cieczy.

Stałą
wystepującą we wzorze można obliczyć mając daną średnicę naczynia D oraz wysokość jego napełnienia cieczą H w stanie spoczynku co ilustruje rysunek:

Z porównania objętości cieczy w spoczynku i w ruchu wynika, że
wobec tego

Korzystając z naszego równania paraboloidy otrzymujemy:

Ostatecznie więc podstawiając do wzoru otrzymujemy równanie opisujące kształt swobodnej powierzchni cieczy w naczyniu o promieniu R, które w stanie spoczynku wypłenione do wysokości H cieczą, wirującym z prędkością kątową

3. Rysunek i opis stanowiska pomiarowego

4. Opis przyrządów i metody pomiarowej

Naczynie napełnione ciecza do wysokości H wprawia się w ruch obrotowy. Po ustaleniu się ruchu należy dokonać bezpośredniego pomiaru prędkości obrotowej n, wysokości z0 oraz wymiaru h powierzchni cieczy.

Pomiary powietrza się kilkukrotnie pryz różnych prędkościach obrotowych naczynia, a następnie bezpośrednio wyznacza się prędkość kątową i obrotową.

Profil teoretyczny

Profil doświadczalny

Wnioski:

a) Celem ćwiczenia było wyznaczenie i porównanie teoretycznego i doświadczalnego profilu równowagi względnej cieczy, a polegało to na tym, że w wirującym walcu znajdowała się ciecz. Wraz ze wzrostem prędkości lustro cieczy zmieniało swój paraboloidalny kształt a zmiany te można było odczytać ze skali.

b) Jak widać na wykresie profil teoretyczny doświadcz. zbytnio się się różnią. Różnice te mogą wynikać np. z braku uwzględnienia lepkości cieczy w obliczeniach, błędem odczytu, a także tym, że wirówka podczas badania wpadała w wibracje co powodowało, że paraboloida była nie stabilna.

1

---