SZKOŁA WYŻSZA

„Mila College”

Wykład 1

Zasady i problemy badań operacyjnych

r.a. 2006/2007

Andrzej B. Chojnacki

SZCZYPTA HISTORII BO

STAROŻYTNOŚĆ

• Aleksander Wielki - falanga

• Archimedes - obrona Syrakuz

PÓŹNIEJ

• Lanchester - równania walki

• Edison - walka z okrętami podwodnymi

• Taylor - wymiary łopaty (twórca zasad naukowej organizacji pracy)

• Levison - handel wewnętrzny

• Erlang - centrale telefoniczne

POWSTANIE BADAŃ OPERACYJNYCH

• Bawdsey Research Station - 1939 - stacje rlok

• Grupa BO przy d-ctwie LM w Stanford - 1940 - rok powstania BO

• Cyrk Blacketta - sierpień 1940: 3 fizjologów, 3 fizyków, 2 matematyków, astronom i oficer

Udział: GB - 365 osób, USA - 400 osób

PO WOJNIE

Ocena wkładu nauki: 1. radar, 2. sonar, 3. BO

• I międzynarodowa konf. BO - 2-7.09.1957 Oxford (Oderfeld + Rajski z IM PAN)

• RAND Corporation - Bellman, Danzig, Teller i wielu innych

ETAPY BADAŃ OPERACYJNYCH

I. Określenie obiektu zainteresowań

(obiektu rzeczywistego)

II. Określenie potrzeby modelowania

matematycznego (formalnego)

i konkretyzacja celu modelowania

III. Budowanie modelu matematycz-

nego (formalnego) uwzględniającego Dokonywanie

cel modelowania poprawek

IV. Formułowanie zadania optymaliza-

cyjnego w języku modelu

V. Rozwiązywanie sformułowanego

zadania optymalizacyjnego

VI. Analiza uzyskanego rozwiązania

VII. Opracowanie projektu

oddziaływania na rzeczywistość

- kolejność podstawowa

- stwierdzenie potrzeby dokonania poprawek

- wprowadzanie poprawek na odpowiednich etapach

KONSTRUOWANIE MODELU MATEMATYCZNEGO

OPIS CECH

M - liczba cech

x_m - symbol zmiennej

X_m - zbiór możliwych wartości zmiennej

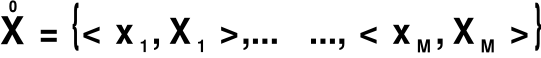
OPIS ZWIĄZKÓW

I - liczba związków

ρ_i - symbol związku

• które cechy występują w i-tym związku ?

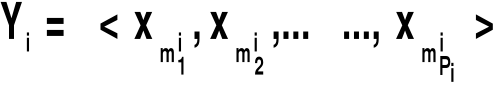
• które wartości cech „spełniają” i-ty związek?

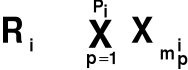
tzn.

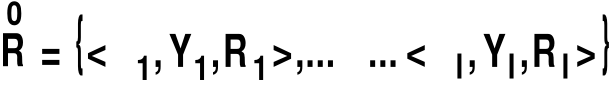
MODEL MATEMATYCZNY

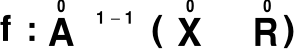
- zbiór nazw cech i związków

lub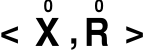

KLASYFIKACJA MODELI MATEMATYCZNYCH

modelowanie decyzja skutki

t

d o p ł y w i n f o r m a c j i

Podział cech z punktu widzenia ich znajomości przez decydenta w chwili podejmowania decyzji:

• 
  znane rozłączne

• nieznane:

• 
  wpływają na nie inni decydenci

• losowe nie

• rozmyte muszą

• nieokreślone być

• przybliżone roz-

• takie, na które decydent ma wpływ: łącz-

• są treścią decyzji (zmienne decyzyjne) ne

• ważne dla celu modelowania (wskaźniki)

• inne

MODELE - kto decyduje

• strategiczne (growe) - są inni decydenci

• optymalizacyjne - nie występują inni decydenci

MODELE OPTYMALIZACYJNE - co decydent wie

• deterministyczne (twarde)

• probabilistyczne/losowe/stochastyczne (niepewność)

• rozmyte (rozmytość)

• w warunkach nieokreśloności (nieokreśloność)

• ze zbiorami przybliżonymi (przybliżoność)

• mieszane

KLASYFIKACJA MODELI MATEMATYCZNYCH - cd.

MODELE OPTYMALIZACYJNE - właściwości cech

• ciągłe

• dyskretne

• mieszane

• czasowe

MODELE OPTYMALIZACYJNE - właściwości związków

• liniowe

• nieliniowe

• wypukłe

• kwadratowe

• dynamiczne

• inne

MODELE OPTYMALIZACYJNE - język modelu

• analityczne

• graficzne

• wariacyjne

• teorii sterowania

• grafowe

• sieciowe

• genetyczne

• neuronowe

• inne

Powyższe klasyfikacje nie stanowią podziałów

ZADANIE OPTYMALIZACYJNE

dane zmienne decyzyjne wskaźniki

funkcja oceny osiągnięcia celu

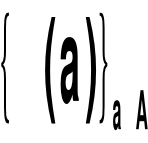
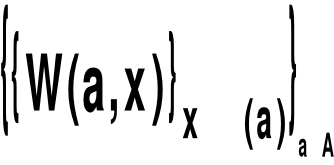
zbiór możliwych zbiór dopuszczalnych zbiór przewidywanych

wartości danych wartości zmiennych wartości wskaźników

decyzyjnych

gdzie:

SFORMUŁOWANIE ZADANIA OPTYMALIZACYJNEGO

Dla danych

wyznaczyć

tak, aby:

- zbiór rozwiązań (dopuszczalnych)

- rozwiązanie optymalne

PROBLEMY:

• pusty zbiór rozwiązań

• zapewnienie istnienia
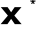
  dla każdego
  

• wieloelementowy zbiór
  

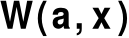
• elementy zbioru
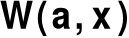
  nie są uporządkowane

• ograniczenia rachunkowe (czas obliczeń, wielkość pamięci)

• brak metod rozwiązywania

• koszt uzyskania rozwiązania

• inne

ANALIZA POZIOMU INFORMACYJNEGO

- dana

- zbiór możliwych (fizycznie) wartości danej

W chwili podejmowania decyzji decydent o danej
będzie mógł powiedzieć, że zna:

• jej wartość

• rozkład prawdopodobieństwa jej wartości

• stopień przynależności jej wartości do zbioru
  

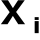
• tylko taki zbiór
  , dla którego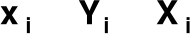
  

• tylko przybliżenie zbioru
  

- zmienna decyzyjna

Nie można mówić o znajomości wartości zmiennej decyzyjnej w chwili podejmowania decyzji, gdyż jest to treścią podejmowanej decyzji

Niech
- zbiór decyzji „twardych”

Możliwe przypadki:

• 
  jest decyzją dopuszczalną

• 
  jest decyzją dopuszczalną z pewnym znanym rozkładem prawdopodobieństwa

• 
  jest decyzją dopuszczalną tylko w znanym stopniu

• 
  jest nieznanym elementem znanego podzbioru zbioru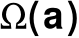
  

• zbiór
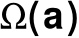
  jest znany w sposób przybliżony

ANALIZA POZIOMU INFORMACYJNEGO (cd.)

- wskaźnik

Nie można mówić o znajomości wartości wskaźnika w chwili podejmowania decyzji, gdyż jest to skutek podejmowanej decyzji

- zbiór wartości wskaźników

Możliwe przypadki:

• zbiór
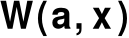
  jest znany w chwili podejmowania decyzji i zawiera wyłącznie jedną liczbę lub wektor liczbowy

• w zbiorze
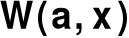
  występują znane rozkłady zmiennych losowych

• w zbiorze
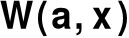
  występują znane funkcje przynależności zmiennych rozmytych

• w zbiorze
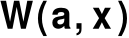
  występują znane zbiory liczbowe

• w zbiorze
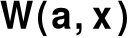
  występują zbiory liczbowe znane w sposób przybliżony

decyzje

dane wskaźniki

DEFINIOWANIE FUNKCJI E_a

zał.: ♦im większa wartość wskaźnika, tym „lepiej”

♦zbiór W(a,x) jest jednoelementowy

W(a,x) = { K(a,x) } = { K }

K:

• liczba

• wektor liczbowy

• zmienna losowa

• zbiór rozmyty

• zbiór liczbowy

• zbiór przybliżony

• ...

K - liczba

Sformułowanie zadania ekstremalizacji

Dla danych

wyznaczyć

tak, aby:

lub:

---