Gimnazjalisto!

Przystępujesz do badania osiągnięć matematycznych z zakresu trzech minionych semestrów nauki w gimnazjum. Przed Tobą zestaw 30 zadań. Zadania czytaj uważnie. Wracaj do tekstów zadań tyle razy, ile to będzie Ci potrzebne. Pamiętaj o zakodowaniu odpowiedzi na karcie odpowiedzi. Kolejność rozwiązywania zadań jest dowolna. Pracuj spokojnie i uważnie. Na rozwiązanie zadań masz 60 minut.

Powodzenia!

Uwaga! Oznaczenie informuje, że zadanie należy rozwiązać na karcie odpowiedzi.

Zadanie 1.

Robert i Monika odrabiali wspólnie pracę domową z matematyki. Obliczając wartość liczbową wyrażenia podanego obok, stwierdzili, że otrzymali różne wyniki. Wykonaj odpowiednie rachunki i ustal, czy któryś z uczniów uzyskał poprawny wynik.

Zadanie 2.

Pani Krystyna, przed wyjazdem do Czech, kupiła w kantorze wymiany walut „PLUS” dolary amerykańskie za łączną kwotę 615zł. W Pradze wymieniła dolary na korony. Ile koron otrzymała pani Krystyna ?

[ A ] 6660 koron [ B ] 7200 koron [ C ] 6765 koron [ D ] 1000 koron

Pan Kowalski przed domem założył trawnik. Zadanie 3.

Przyjmując, że długość kratki wynosi 1m oraz π ≈ 3 ustal jaka jest powierzchnia trawnika ?

[ A ] 72m ² [ B ] 73m ² [ C ] 74m ² [ D ] 75m ²

Zadanie 4.

Korzystając z informacji zawartych na opakowaniu, oblicz ile dag mieszanki trawnikowej wysieje pan Kowalski ?

[ A ] 1,875 dag [ B ] 18,75 dag [ C ] 187,5 dag [ D ] 1875 dag

Zadanie 5.

Przyjmując założenia z zadania 3, oblicz jakim procentem powierzchni całego trawnika jest jego prostokątna część ?

[ A ] 64% [ B ] 50% [ C ] 36% [ D ] 21,2%

Zadanie 6.

Spadek swobodny ciała wyraża się wzorem:
, gdzie h oznacza wysokość, z której ciało spada, g - przyspieszenie ziemskie, a t - czas spadania. Który wzór opisuje czas spadania ?

[ A ]
[ B ]
[ C ]
[ D ]

Zadanie 7.

Jeśli przyjmiemy, że x = 5,2 m oraz y = 20dm, to pole wyróżnionej części trapezu wynosi:

Zadanie 8.

Rysunek przedstawia trapez równoramienny. Które z podanych wyrażeń opisuje obwód trapezu ?

[ A ] 4x - 6y [ B ] 2(3x + 2y) [ C ] 4x + 6y [ D ] 2(3x - 2y)

Zadanie 9.

Jeśli powierzchnię z odpowiedzi [ B ] zadania 7, wyrazimy w arach i przedstawimy ją w notacji wykładniczej, to otrzymamy:

[ A ] 4,1 ⋅ 10 ² a [ B ] 3,6 ⋅ 10 ^-1 a [ C ] 1,2 ⋅ 10 ^-1 a [ D ] 0,36 ⋅ 10 ² a

Marek jest pięć razy młodszy od mamy. Gdybyśmy Markowi doliczyli 12 lat, a jego mamie zabrali 12 lat, to okazałoby się, że są w tym samym wieku.

Zadanie 10.

Jeśli przez x oznaczymy wiek syna, a przez y - wiek mamy, to który układ równań opisuje tę sytuację.

Zadanie 11.

Ile lat ma Marek, a ile jego mama ?

Diagram przedstawia średnie miesięczne temperatury powietrza zanotowane w Gdańsku w 1999 roku.

Zadanie 15.

Średnia temp. powietrza w II kwartale tego roku wyniosła ?

[ A ] 1,8 ^o C [ B ] - 14 ^o C [ C ] 13 ^o C [ D ] - 22 ^o C

Zadanie 16.

Różnica pomiędzy najniższą, a najwyższą temp. zanotowaną w ciągu wskazanego roku wyniosła:

[ A ] - 13 ^o C [ B ] - 33 ^o C [ C ] 1,3 ^o C [ D ] 33 ^o C

Zadanie 17.

W wielu krajach temperaturę mierzy się w stopniach Fahrenheita. Jeżeli C oznacza liczbę stopni w skali Celsjusza, a F odpowiednią liczbę stopni w skali Fahrenheita, to F = 9 ⋅ C : 5 + 32.

Ustal jaka była średnia temperatura w stopniach Fahrenheita w lutym 1999 roku, w Gdańsku.

[ A ] 19,4 [ B ] - 12,7 [ C ] 44,6 [ D ] - 13

Zadanie 18.

Śmietana stanowi 25% przerobionego mleka, a masło 20% śmietany. Ile potrzeba kg mleka, aby otrzymać 50 kg masła ?

[ A ] 540 [ B ] 1000 [ C ] 980 [ D ] 1100

Zadanie 20.

Do Klubu Młodych Przyrodników zapisało się x uczniów z klasy I a, oraz tyle samo uczniów z klasy II b. Uczniów z klasy II c jest w klubie o y więcej, niż uczniów z klasy II b. Ilu uczniów należy do klubu ?

[ A ] 3x + y [ B ] 3(x + y) [ C ] 3x - y [ D ] 3y + x

Zadanie 21.

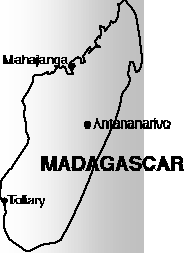
Na mapie w skali 1 : 40 000 000, długość wyspy Madagaskar wynosi 4cm. Jaką w przybliżeniu długość ma ta wyspa w rzeczywistości ?

[ A ] 1200km [ B ] 800km [ C ] 1000km [ D ] 1600km

Zadanie 22.

Madagaskar, to państwo afrykańskie lezące na wyspie o tej samej nazwie, na Oceanie Indyjskim. Wyspę zamieszkuje ok. 14,3 mln mieszkańców (dane z 1994 ). Jeśli wiadomo, że na jednego mieszkańca wyspy przypada ok. 4,1 ha, to jaką w przybliżeniu, powierzchnię, w km ² ma ta wyspa ?

[ A ] 56,8 tyś. km ² [ B ] 586,3 tyś. km ² [ C ] 600,8 tyś. km ² [ D ] 90,84 tyś. km ²

Zadanie 23. Odszukaj zdanie, które jest nieprawdziwe.

[ A ] Trójkąty przystające mają odpowiednie boki tej samej długości.

[ B ] Kąty naprzeciwległe w równoległobokach mają równe miary.

[ C ] W każdym rombie przekątne są prostopadłe i równej długości.

[ D ] W trójkącie prostokątnym suma kątów ostrych wynosi 90^o.

Zadanie 24.

Wysepka na skrzyżowaniu ma kształt kwadratu. Korzystając z własności przekątnych w rombie, oblicz pole wysepki przyjmując, że długość przekątnej wysepki wynosi 4
m.

Zadanie 26.

Kuba, Marcin i Wojtek, podczas wakacyjnej wędrówki po Europie wykonali szereg ciekawych zdjęć. Razem chłopcy wykonali 225 fotografii. Marcin wykonał dwa razy więcej zdjęć od Kuby, który zrobił o 9 zdjęć mniej od Wojtka. Ustal ile zdjęć wykonał każdy z podróżników ?

[ A ] 51, 66, 108 [ B ] 81, 54, 90 [ C ] 63, 72, 80 [ D ] 108, 63, 54

Zadanie 27.

Oblicz obwód przedstawionej poniższej figury.

[ A ] 20 ( 10 + 3 π ) [ B ] 240 π + 60

[ C ] 200 - 60 π [ D ] 20( 3 π - 10 )

Zdobywanie wiedzy

jest jak zdobywanie szczytów.

Test osiągnięć matematycznych

uczniów klas II

Gimnazjum w Dąbrówce

skup sprzedaż

DEM 1,90 2,05 USD 3,95 4,10

[
] : (- 1,2) =

wynik: MONIKI ROBERTA

- 1
3,4

KANTOR „PLUS”

KANTOR „VICO”

skup sprzedaż

USD 45,1 45,3 DEM 22,2 22,6

80

Zadanie 29.

Uzasadnij, że liczba:

3 ^{n + 2} - 2 ^{n + 2} + 3 ⁿ - 2 ⁿ

jest wielokrotnością liczby 10, dla każdej liczby naturalnej n.

trawnik

0,5 kg

na 20m²

Mieszanka

trawnikowa

2x

Zadanie 25.

Laborant przygotowuje roztwór soli. Ile gramów 20% roztworu soli trzeba zmieszać z 10 gramami 10% roztworu soli, aby otrzymać roztwór 15% ?

[ A ] 5 g [ B ] 3,5 g [ C ] 10 g [ D ] 15 g

Zadanie 28.

Cenę spodni, kosztujących 250 zł, w wakacyjnej promocji, obniżono o 12%.

a) Podaj wielkość obniżki ceny spodni.

b) Ustal nową cenę spodni.

zadania na ocenę celującą

Warunkiem uzyskania oceny celującej jest uzyskanie oceny bardzo dobrej z podstawowej części testu oraz prawidłowe rozwiązanie jednego z dwóch proponowanych zadań na ocenę celującą.

Zadanie 19.

Adam w czasie 4 minut pokonuje 250m. Jaką drogę (w km) pokona chłopak w ciągu dwóch godzin ?

[ A ] 7,5 [ B ] 6,4 [ C ] 9,3 [ D ] 5,5

x

•

2x + 1

x - y -1

%

[ A ]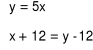

[ A ] 4,4 m² [ B ] 36 m² [ C ] 10,5 m² [ D ] 6,5 m²

3y

2y

[ B ]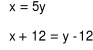

WERSJA A

[ D ]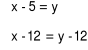

[ C ]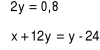

odpowiedzi	[ A ]	[ B ]	[ C ]	[ D ]
wiek Marka	7	10	12	6
wiek mamy	35	50	36	30

Zadanie 12.

Rozwiąż poniższe równanie:

(x - 5) ² + 2x ≥ x ² - 3(x + 2) .

a) Rozwiązanie przedstaw na osi liczbowej.

b) Podaj najmniejszą liczbę całkowitą, która nie spełnia tej nierówności.

Zadanie 13.

Kąt α ma miarę:

[ A ] 94⁰ [ C ] 164⁰

[ B ] 82⁰ [ D ] 196⁰

98^o

α

•

Zadanie 14.

Długość Kanału Panamskiego wynosi 80km. W jakim czasie przepłynie ten kanał statek płynący ze średnią prędkością 16 węzłów ?

Przyjmij, że 1 węzeł ≈ 1,9 km / h

[ A ] ok. 22h 41min [ B ] ok. 4h 55min

[ C ] ok. 37h 19min [ D ] ok. 2h 36min

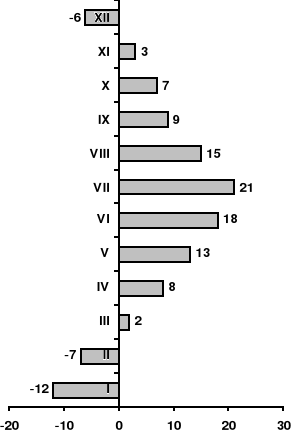
temperatura ^o C

miesiące

Zadanie 30.

Wykaż, że w dowolnym trójkącie dwusieczne jego kątów wewnętrznych nie są wzajemnie prostopadłe. Wykonaj odpowiedni rysunek poglądowy oraz stosowne obliczenia.

Powodzenia!

---