Zad. 1. (9 pkt.) Czy następująca funkcja zdaniowa:
[ (A ∩ B) \ C ≠ A ∪ B ] ∨ [ ∼ ( A ⊆ C) ] ∨ [ C = ∅ ]
jest prawdziwa dla każdych trzech podzbiorów zbioru {1,2,3}? (Tak/Nie)? ......Nie
Jeśli odpowiedziałeś "Nie", przedstaw kontrprzykład przez wskazanie trzech (niekoniecznie różnych) zbiorów A, B, C ⊆ {1, 2, 3}, dla których ta funkcja staje się zdaniem fałszywym.
Kontrprzykład (opcjonalnie): A = ................ ∅....................... B = ................. ∅...................... C = ..................{1}..................... (istnieje więcej kontrprzykładów)
Zad. 2. (9 pkt.) Uzupełnij poniższe formuły symbolami zmiennych zdaniowych tak, aby powstałe schematy logiczne były logicznie równoważne schematowi (p ∨ r) → (~p). Możesz używać wyłącznie symboli zmiennych zdaniowych (np. p, q, r, s). Dopisywanie spójników logicznych jest niedozwolone. Jeżeli uważasz, że w którymś przypadku takie uzupełnienie nie jest możliwe, wpisz obok formuły sformułowanie "brak rozwiązania".
(a) np.: (.q....∧ ~ ..q...) ∨ (~..p... ) (b) ..... brak rozw. (c) (~..p... )
Zad. 3. (9 pkt.) Uniwersum jest zbiorem studentów. Definiujemy następujące predykaty: Z(x) - x zdał egzamin z matematyki; W(x) - x chodził na wykłady z matematyki; L(x, y) - x lubi matematykę bardziej niż y; R(x, y) - x i y to ten sam student.
Wyraź w języku rachunku predykatów pierwszego rzędu następujące zdania: (a) Dokładnie jeden student zdał egzamin z matematyki. (b) Żaden, spośród studentów, którzy nie chodzili na wykłady z matematyki, nie zdał egzaminu z tego przedmiotu (c) Co najmniej dwóch studentów zdało egzamin z matematyki. Nie wolno używać żadnych innych symboli niż: nawiasy, wymienione powyżej predykaty, zmienne, kwantyfikatory oraz spójniki logiczne.
(a) .....np.: ∃x(Z(x)) ∧ ∀Z(x) ( ∀Z(y) (R(x, y)))
(b) np.: ∀x((~W(x)) → (~Z(x)))
(c) np.: ∃Z(x) (∃Z(y)(~R(x, y)))
Zad. 4. (9 pkt.) Poprzez wskazanie kontrprzykładu, udowodnij, że porządek leksykograficzny nie musi być dobrym porządkiem. Rozwiązanie przedstaw na odwrocie strony.
Niech Σ = {a, b} i a ≤ b. Niech xn oznacza słowo składające się z n liter x. Np. x3 = xxx. Niech A = {anb : n ≥ 0}. W zbierze A nie istnieje element najmniejszy, gdyż dla dowolnego słowa akb jstnieje słowo mniejsze ak+1b (np. dla k = 3, leksykagroficznie wcześniej znajduje się słowo aaaab niż słowo aaab). Przykład ten był omawiany na wykładzie.
Zad. 5. (9 pkt.). W zbiorze A = {1, 2, ..., 10} zdefiniowano relację binarną S:
xSy ⇔ ( x < y ∧ x | y + 2 ).
Niech R = p(z(S)). Dla zbioru częściowo uporządkowanego (A, R) Wyznacz:
(a) Wszystkie elementy minimalne: ....................1.......................................................................................................
(b) Wszystkie elementy maksymalne:.....................7, 8, 9, 10....................................................................................................
(c) Najliczniejszy antyłańcuch, zawierający liczbę 2: .............2, 3, 5, 9 lub 2, 5, 7, 9.....................................................................................
Na odwrocie przedstaw diagram Hassego tego porządku.
Zad. 6. (10 pkt.) Dla grafu przestawionego powyżej wyznacz:
(a) Wagę minimalnego drzewa spinającego: ............13.........................
(b) Długość optymalnej trasy chińskiego listonosza:...............62 + 7 = 69......................
(c) Długość optymalnej trasy komiwojażera (długość najkrótszego cyklu Hamiltona) :........28.........
(d) Liczbę chromatyczną :.....4............
Zad. 7. (10 pkt.) Wyznacz liczbę podgrafów pełnego grafu K10, które są izomorficzne z grafem:
(a) K1,9: ........................10..................................... (b) C8: ........ 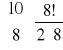
.......................................................................
(c) K5,5: ..................![]()
.......................................... (d) K4: ......... ![]()
.......................................................................