1. Pojęcia podstawowe: punkt materialny, układ punktów materialnych, ciało sztywne, więzy i ich klasyfikacja, stopień swobody układu, ilość stopni swobody poruszającego się bez ograniczeń punktu materialnego oraz ciała sztywnego

Punkt materialny - punkt geometryczny o pewnej skończonej masie mający na płaszczyźnie dwa, a w przestrzeni trzy stopnie swobody

Układ punktów materialnych - ciało zawierające dowolną liczbę punktów materialnych

Ciało sztywne - ciało stałe, którego punkty nie zmieniają wzajemnych odległości pod wpływem działających na nie sił.

Więzami nazywamy warunki ograniczające ruch ciała w przestrzeni

Rodzaje więzów: Dwustronne i jednostronne.

Stopniem swobody nazywa się możliwość wykonywania ruchu ciała niezależnego od innych ruchów, punkt materialny ma na płaszczyźnie dwa, a w przestrzeni trzy stopnie swobody, ciało sztywne ma na płaszczyźnie trzy, a w przestrzeni sześć stopni swobody.

2. Czas, przestrzeń, siła, ruch, materia, masa

Czas - cechą charakterystyczną czasu jest nieodwracalność jego płynięcia, które ma tylko jeden kierunek, ma tylko jeden wymiar.

Przestrzeń - pod pojęciem tym rozumie się przestrzeń euklidesową, ma trzy wymiary odległości, mierzone w trzech wzajemnie do siebie prostopadłych kierunkach (długość, szerokość, wysokość)

Masa jest jednocześnie miarą ilości materii zawartej w ciele i miarą bezwładności ciała. Jednostką masy jest 1 kg.

Siła jest miarą wzajemnego oddziaływania ciał, przejawiającego się wyprowadzeniem ich ze stanu spoczynku, zmiany ich ruchu lub utrzymaniem ciał w stanie równowagi

Ruchem ciała nazywamy zachodzące w czasie zmianę jego położenia względem innego ciała, które umownie przyjmujemy za nieruchome.

3. Statyka, Pojęcie siły, Prawa statyki

Statyka jest szczególnym przypadkiem dynamiki polegającym za tym, że siły działające na ciało materialne znajdują się w równowadze, co oznacza, że ciało jest w spoczynku lub porusza się ruchem jednostajnym prostoliniowym

Prawa statyki

• zasada pierwsza (zasada równoległoboku) działanie dwóch sił P₁ i P₂ można zastąpić działaniem jednej siły R, działającej na ten sam punkt, będącej przekątną równoległoboku zbudowanego na wektorach sił P₁ i P₂

• zasada druga, jeżeli do ciała przyłożone są dwie siły, to równoważą się tylko wtedy, gdy mają tę samą linię działania te same wartości liniowe i przeciwne zwroty

• zasada trzecia, skutek działania dowolnego układu sił, przyłożonych do ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny układ równoważących się sił, czyli tzw. Układ zerowy

• zasada czwarta (zasada zesztywnienia) jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne) identycznie z poprzednim pod działaniem tego samego układu sił

• zasada piąta (zasada działania i przeciwdziałania) każdemu działaniu towarzyszy równe co do wartości o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie

• zasada szósta (zasada oswobodzenia z więzów) każde ciało nieswobodne można myślowo oswobodzić z więzów zastępując ich działanie reakcjami, a następnie rozpatrywać jako ciało swobodne znajdujące się pod działaniem sił czynnych i biernych

Układ sił - wzajemne oddziaływanie więcej niż dwóch brył

4.Układy sił. Wielobok sił - konstrukcja

Układ sił - wzajemnie oddziaływanie więcej niż dwóch brył.

Wielobok sił.

7.Pojęcie momentu sił względem punktu i prostej (osi)

Moment siły względem punktu - nazywamy odłożony z punktu O wektor M_o równy iloczynowi wektorowemu promienia wektora R i wektora siły M_o = R x P

Moment siły względem osi - rzut wektora momentu siły względem dowolnego punktu osi na tę oś.

8.Pojęcie równowagi ciała

Warunek równowagi ciała, punktu materialnego lub układu punktów materialnych znajdują się w równowadze jeżeli działające na nie siły równoważą się

9.Płaski dowolny układ sił, Redukcja sił, Moment główny, Wektor główny, Wyrażenia analityczne

Płaski dowolny układ sił - redukcja, w przypadku, gdy suma geometryczna układu sił P₁ i P₂ ... P_n działających w jednej płaszczyźnie na ciało sztywne różna jest od zera, układ możemy zastąpić jedną siłą wypadkową, równą wektorowi głównemu R, a jeżeli jest równa zero, to układ sił może, ale nie musi redukować się do pary sił, której wektor jest prostopadły do płaszczyzny działania sił gdy W_g i M_g ≠ 0 skrętnik; W_g ≠ 0, M_g = 0 wektor gł. W_g = 0, M_g ≠ 0 para sił;

Wektor główny R przesuwając równolegle wszystkie siły danego układu do jednego punktu O otrzymamy jedną siłę R równą sumie geometrycznej.

Moment główny M_o - jedna para sił o momencie M_o równym sumie momentów tych par sił (względem obranego bieguna jest równy sumie geometrycznej momentu głównego tego układu względem pierwotnego bieguna.

10. Szczególne przypadki redukcji: płaskiego dowolnego układu sił, zbieżnego układu sił, Wektorowe i skalarne warunki równowagi

Warunki równowagi płaskiego dowolnego układu sił jeśli sumy rzutów wszystkich sił na osie układu są równe zero i moment wszystkich sił względem dowolnego punktu płaszczyzny działania sił jest równy zero - jeżeli moment układu sił względem dwóch punktów jest równy zero oraz rzut sił na oś nie prostopadłą do odcinka łączącego te punkty jest równy zero - jeżeli moment układu sil względem trzech punktów nie leżących na jednej prostej jest równy zero.

11. Płaski równoległy układ sił, Redukcja, Warunki równowagi

Warunki równowagi płaskiego równoległego układu sił - pierwsze z równań równowagi jest spełnione tożsamościowo i i pozostałe dwa równania równowagi

ΣP_i = ΣP_y = 0, ΣM_i0=0, ΣM_iA=0, ΣM_iB=0, M_o = ΣM_i0=ΣP_i X_i

12.Przestrzenny dowolny układ sił, Redukcja, Warunki równowagi

Redukcja dowolnego przestrzennego układu sił - układ możemy zastąpić siłą R przyłożoną do dowolnego wybranego środka redukcji O, równą sumie geometrycznej wszystkich sił układu oraz pary sił o momencie M_o równym sumie geometrycznej momentów tych sił względem środka redukcji.

Skrętnik - układ złożony z wektora głównego R, składowej momentu głównego M_o leżącego na linii działania wektora R.

Redukcja do dwóch sił skośnych, z których jedna przechodzi przez środek redukcji O

Redukcja do siły wypadkowej - warunkiem jest istnienie różnej od zera sumy geometrycznej R, prostopadłość wektora momentu głównego M_o względem dowolnie wybranego punktu O do linii działania sumy geometrycznej.

Redukcja do pary sił - gdy wektor główny równa się zeru natomiast moment główny M_o względem dowolnego punktu o nie jest równy zero, moment jest równy momentowi głównemu układu.

Warunki równowagi - jeżeli suma geometryczna R jest równa zero oraz moment główny M_o układu względem dowolnego punktu O jest równy zero - jeżeli suma rzutów wszystkich sił na trzy osie układu równa jest zero i suma momentów wszystkich sił względem trzech osi układu jest równa zeru.

21. Jak określamy ruch płaski bryły. Podstawowe własności ruchu płaskiego. Ruch płaski jako ruch złożony. Określenie prędkości i przyspieszeń przez składanie chwilowego ruchu postępowego i obrotowego

Ruchem płaskim bryły nazywamy ruch, podczas którego wszystkie punkty ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny zwanej płaszczyzną kierującą . Badanie ruchu płaskiego ciała płaskiego ciała sztywnego sprowadza się do badania ruchu figury płaskiej poruszającej się w swej płaszczyźnie. W układzie współrzędnych określamy chwilowe położenie figury za pomocą współrzędnych xi y dowolnego punktu figury. Gdy rozważana figura porusza się w płaszczyźnie Oxy współrzędne x, y oraz kąt φ są pewnymi funkcjami czasu.

Równania ruchu figury płaskiej mają postać:

1. Dowolne przemieszczenie figury płaskiej w płaszczyźnie może być dokonane za pomocą przesunięcia równoległego, równego przesunięciu dowolnie obranego punktu A tej figury, oraz obrotu wokół tego punktu. Kąt obrotu nie zależy przy tym od wyboru punktu A.

2. Dowolne przemieszczenie figury płaskiej w jej płaszczyźnie może być dokonane za pomocą obrotu wokół pewnego punktu zwanego środkiem obrotu (obrotowi wspomnianej figury wokół środka C odpowiada obrót ciała wokół osi obrotu przechodzącej przez pkt. C i przechodzącej prze punkt C i prostopadłej do płaszczyzny tej figury).

Ruch płaski jako ruch złożony z ruchu postępowego i obrotowego

Ruch figury płaskiej w płaszczyźnie może być traktowany jako ruch złożony z ruchu postępowego, którego prędkość jest równa prędkości obranego bieguna A oraz ruchu obrotowego figury wokół tego bieguna. Prędkość kątowa ruchu obrotowego figury nie zależy od wyboru bieguna

przyspieszenie kątowe

Prędkość dowolnego punktu B figury płaskiej, poruszającej się w swej płaszczyźnie, równa jest sumie geometrycznej prędkości dowolnie obranego punktu A tej figury, zwanego biegunem oraz prędkości B względem punktu A.

V_B = V_A + V_A/B V_A/B = ω x r_AB

Wektor przyspieszenia jest skierowany prostopadle do płaszczyzny w której dana figura się porusza.

22. Co to jest chwilowy środek obrotu. Metody wyznaczania chwilowego środka obrotu

W rozpatrywanej przez nas chwili punkty badanej figury płaskiej mają takie same prędkości, jakie miał gdyby w ruchu obrotowym tej figury wokół punktu C. Punkt ten nazywamy środkiem obrotu chwilowego lub środkiem chwilowym. Chwilowemu ruchowi obrotowemu figury wokół środka chwilowego C odpowiada chwilowy ruch obrotowy ciałą sztywnego wokół osi chwilowej przechodzącej przez punkt C i prostaopadłej do płaszczyzny, w której wspomniana figura porusza się.

rys

Dla wyznaczenie chwilowego środka obrotu nie jest konieczna znajomość prędkości punktów A i B. Aby móc wykonać konstrukcję geometryczną, musimy znać proste, wzdłuż których skierowane są w rozpatrywanej chwili prędkości V_A i V_B czyli muszą być styczne do torów punktów A i B. Gdy wektory V_A i V_B są do siebie równoległe , wówczas środek chwilowy leży w nieskończoności ω = 0. Gdy prędkości V_A i V_B są prostopadłe do prostej łączącej punkty A i B, wówczas wartości tych prędkości mogą być dowolne.

rys

32) Zasada prac wirtualnych.

Warunkiem Koniecznym równowagi n punktów materialnych przy danych siłach działających F_i jest znikanie pracy przygotowanej tych sił

- przesunięcie wirtualne (pomyślane przesunięcie zgodne z więzami nałożonymi na ruch) punktu materialnego (Lagrange'a). Zasada D' Alamberta

33) Ruch postępowy jednostajnie przyspieszony

x = x₀ + v₀t +

x = x₀ + v₀t

Ruch obrotowy jednostajnie przyspieszony

θ = θ ₀ + ω₀t +

ω = ω₀ + αt

ruch postępowy i ruch obrotowy

F = ma =
Γ = Iα =

E_k = ½ mv² E_k = ½ Iω²

Popęd FΔt = p_c - p₀ Γ Δt = l_k - l₀

F_s - składowa siły wypadkowej w kierunku przesunięcia

1. Jeżeli całkowitą wykonaną pracę podzieli się na kategorie zgodnie z typami sił wykonujących pracę, ogólna zależność pomiędzy pracą i energią

W_a = (E_k - E_k0) + (U + U₀) + Q

W_a - praca wykonana przez siły przyłożone

Q - energia utracona w wyniku sił tarcia

U i U₀ - energia potencjalna

W specyficznych warunkach, kiedy nie działają ani siły tarcia, zarówno W_a = 0 i Q = 0 i mówimy o zachowaniu energii mechanicznej układu.

E_k + U = E_k0 + U₀

Jeżeli energia mechaniczna jest zachowana E = E_k + U pozostaje stała, chociaż E_k i U mogą się zmieniać.

Dynamika punktu materialnego

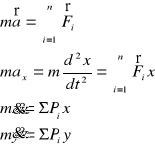
26. Położenie środka ciężkości

x = x₁w₁ + x₂w₂ + x₃w₃ +...

w = w₁ + w₂ + w₃ +...

Jeżeli każdy ciężar wyrazimy w postaci w = mg, g ulegnie uproszczeniu i x xależy wtedy nie od ciężaru ale od masy i nazywane jest środkiem masy.

Nie ma różnicy pomiędzy położeniem środka masy i środka ciężkości o ile g ma ten sam kierunek i wartość dla każdego ciężaru.

27. Moment bezwładności - wielkość fizyczna charakteryzująca rozkład masy ciała; może być określany względem punktu lub osi; masowej moment bezwładnośći układu punktów materialnych (bryły) względem osi z określa się wzorem;

I =
- odległość od osi m - masa i-tego punktu materialnego

Dla każdego ciała obracającego się wokół stałej osi wypadkowy moment siły równy jest iloczynowi momentu bezwładności tego ciała i przyspieszenia kątowego.

Krążek;
pręt

walec;
kula

Dla ciał nieregularnych tj. kość czy piramidę, konieczne jest doświadczalne wyznaczenie momentu bezwładności.

Także eksperymentalne wyniki są często wyrażane przez podanie masy m i promienia bezwładności

I = mk² => k =

23.Dynamika, Prawa Newtona, Dynamika punktu materialnego, Równania dynamiki punktu materialnego

Dynamika - dział mechaniki badający ruch ciał materialnych pod wpływem działających tam sił. W zależności od względnych prędkości ciał dzieli się na d. relatywistyczna i klasyczną. W zależności od badanych obiektów; punktu materialnego, układu punktów materialnych, ciała sztywnego, o zmiennej masie itd.

Do podstawowych pojęć: punkt materialny, masa, siła, ciało sztywne, pęd, popęd, energia.

Prawa Newtona:

I - Jeżeli na ciało nie działają żadne siły lub jeśli działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym

II - Zmiana pędu ciała jest proporcjonalna do przyłożonej siły

III - Każdemu działaniu towarzyszy równe mu lecz przeciwnie skierowane przeciwdziałanie

1)

2)

3)

24. Dynamiczne równania ruchu nieswobodnego punktu materialnego, Dwa podstawowe zagadnienia mechaniki, związek pomiędzy momentem skręcającym, mocą i prędkością obrotową

25. Pęd i popęd, Kręt i pokręt, Zasada zachowania pędu i popędu dla punktu materialnego,

Pęd - pęd punktu materialnego o masie m i prędkości V równy jest
. Pęd układu mech. jest sumą wektorową pędów poszczególnych punktów układu lub iloczynem całkowitej masy M układu przez prędkość V_c jego środka masy M

Zasada zachowania pędu
- pęd zamkniętego układu mech. tj. takiego, na który nie działają siły zewnętrzne pozostaje wielkością stałą. Siły wew. nie mogą zmieniać całkowitego pędu układu, choć pędy ciał mogą ulec zmianie.

Popęd - wielkość fizyczna charakteryzująca działanie wywierane na ciało przez siły F w ciągu pewnego czasu Δt
; jeśli siła działająca zmienia się z czasem,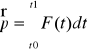
; popęd siły wywieranej na ciało równa się zmianie pędu ciała.

Kręt (moment pędu)- wielkość charakteryzująca ruch ciała (układu) zwłaszcza ruch obrotowy. Jest określony iloczynem wektorowym
r- wektor wodzący od punktu O do P bryły sztywnej względem osi, wokół której obraca się z prędkością kątową

J- moment bezwładności

26. Praca-wielkość fizyczna określająca wartość energii wydatkowanej na przemieszczenie ciała materialnego z jednego położenia do drugiego

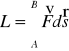
- wektorowy element drogi

jeśli
= const, ciało porusza się ruchem jednostajnie prostoliniowym

Moc - wielkość charakteryzująca układ wykonujący pracę lub wysyłający energię; moc średnia jest równa stosunkowi pracy L do czasu Δt, w którym ta praca została wykonana M_śr = L/t

Energia kinetyczna - część energii mechanicznej układu zależna od prędkości jego punktów; w przypadku ciała sztywnego o masie spoczynkowej m₀ poruszającego się ruchem postępowym z prędkością v

13. Tarcie, Tarcie statyczne i kinematyczne, Tarcie poślizgowe i tarcie toczne

Tarcie - zjawisko powstawania sił stycznych do powierzchni styku dwóch ciał.

Tarcie statyczne zależy od rodzaju materiału trących się ciał, chropowatości i stanu ich powierzchni (suche, wilgotne, zimne, gorące) tarcie kinematyczne zależy od względnej prędkości ciała.

Stożek tarcia - tarcie nie zależy od kierunku działania siły T, wobec tego reakcja R może leżeć w każdej z płaszczyzn przechodzących przez normalną O_r i odchylać się od tej normalnej o kąt tarcia φ.

14. Kinematyka, Pojęcie ruchu, Tor, Sposób opisu ruchu bryły oraz punktu materialnego

Torem lub trajektorią punktu nazywamy miejsce geometryczne kolejnych położeń tego punktu w przestrzeni.

Opis ruch:

- za pomocą wektora promienia wodzącego

• za pomocą równań skończonych ruchu x= f₁(t), y = f₂(t) z = f₃(t)

• za pomocą współrzędnej naturalnej

• za pomocą innych współrzędnych

15.Równania ruchu punktu, Wyznaczenie prędkości i przyspieszenia przy opisie ruchu za pomocą równania wektorowego we współrzędnych prostokątnych

16.Współrzędne naturalne, wektor krzywizny, trójścian Freneta, Rozkłąd przyspieszenia na kierunki naturalne

17.Ruch punktu po okręgu

[m/s]


[s^-1]

18.Klasyfikacja ruchu punktu z uwagi na tor prędkość i przyspieszenie

19.Ruch bryły. Proste przypadki ruchu bryły. Ruch postępowy - równania. Wielkości charakteryzujące

Jeżeli bryła porusza się ruchem postępowym to wszystkie punkty bryły poruszają się po torach przystających i w każdej chwili mają te same wektory prędkości przyspieszenie.

20.Ruch obrotowy bryły wokół osi nieruchomej - równania ruchu, Wielkości charakteryzujące. Zależności pomiędzy prędkością kątową, prędkością liniową, ilością obrotów i średnicą toru (koła)

5.Dwie siły równoległe. Wypadkowa dwóch sił równoległych o wartościach równych zgodnie skierowanych oraz o różnych wartościach przeciwnie skierowanych.

Działanie siły na ciała sztywne nie ulegają zmianie jeżeli przesunie się siłę wzdłuż jej prostej działania do innego punktu położenia

W=
rysunki

Rozkład sił na dwa kierunki

rys

rozkład sił na trzy kierunki

Można go przeprowadzić tylko wówczas, gdy trzy kierunki na które rozkładamy siłę nie są do siebie równoległe i nie przecinają się w jednym punkcie.

rys

Siły przyłożone do brył lub punktów materialnych możemy podzielić na siły zewnętrzne i wewnętrzne. Siły zewnętrzne są to siły przyłożone do poszczególnych brył pochodzące od brył nie wchodzących w skład rozpatrywanego układu.

Drugą grupą sił są siły pochodzące od więzów w przypadku gdy bryła jest nieswobodna. Siły te nazywamy siłami reakcji.

Siły wewnętrzne to siły, z jakimi oddziaływują na siebie poszczególne bryły lub punkty materialne wchodzące w skład danego układu, wzajemne oddziaływanie brył określa III prawo Newtona.

Środkowy układ sił - układ sił, w którym proste działania przecinają się w jednym punkcie. Taki układ można zastąpić jedną siłą, którą nazywamy wypadkową tego układu, sprowadzić do dwójki zerowej (układ jest w równowadze).

Jeżeli wielobok sił(suma geometryczna) jest zamknięty to układ środkowy pozostaje w równowadze. Jeżeli wielobok sił jest otwarty to układ środkowy ma wypadkową . Wektor główny (
) to wektor zamykający wielobok sił.

Trzy siły są w równowadze, jeżeli ich proste działania przecinają się w jednym punkcie, leżą w jednej płaszczyźnie i trójkąt sił jest trójkątem zamknięty.

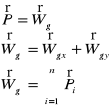
Aby układ znajdował się w równowadze

Warunkiem koniecznym i wystarczającym równowagi przestrzennego środkowego układu sił jest, aby algebraiczne sumy rzutów wszystkich sił na osie układu współrzędnych były równe zero

6.Pojęcie pary sił, Wektor i moment pary sił, Umowa znaków

Para sił - dwie siły równe co do wartości, równoległe leżące w jednej płaszczyźnie, skierowane przeciwnie

Moment pary sił to wektor prostopadły do działania pary sił jest niezależny od wyboru punktu, jest wielkością stałą, a jego wartość równa się iloczynowi wartości jednej z sił pary i odległości między siłami

Tw1. Działanie pary sił na ciało sztywne nie ulegnie zmianie gdy parę przeniesiemy w dowolne położenie w płaszczyźnie jej działania

Tw2. Działanie pary sił na ciało sztywne nie ulegnie zmianie gdy zmienimy siły pary i ramię tak aby wektor momentu został niezmieniony

Tw3. Działanie pary sił na ciało sztywne nie ulegnie zmianie gdy parę przesuniemy na płaszczyznę równoległą do jej płaszczyzny działania.

Energia potencjalna - część energii mechanicznej zależna od wzajemnego rozmieszczenia części układu i od ich położenia w zewnętrznym polu sił. Miarą jest praca, którą muszą wykonać siły działające na układ, aby przeprowadzić go z danego położenia do położenia dla którego energię potencjalną przyjmuje się za równą zeru.

E_p = mgh

28. Zasada zachowania energii

Całkowita energia dowolnego izolowanego układu ma wartość stałą. W procesach fizycznych jedna forma energii może zmienić się w inną, np. energia mechaniczna w energię cieplną, ale całkowita energia pozostaje zawsze stała.

Zasada równoważności pracy i energii.

2. Całkowita praca wykonana przez wszystkie siły działające na ciało, równa jest zmianie energii kinetycznej ciała, E_k - E_k0,

W = E_k - E_k0,

W= F_s*s, gdzie :

s- przesunięcie ciała

---