22. Obliczanie wytrzymałościowe spoin czołowych, naprężenia w spoinie ukośnej oraz w spoinie czołowej z nakładkami.

Spoina ukośna

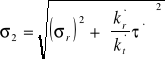
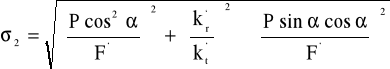
- naprężenia zastępcze

Połączenie czołowe z dwiema nakładkami

F - przekrój pręta

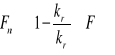
23. Obliczanie wytrzymałościowe dwuteownika połączonego spoiną czołową z nakładkami obciążonego momentem zginającym. Gdzie należy umieścić nakładki i dlaczego?

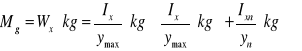
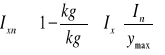
kg` - naprężenia dopuszczalne na zginanie dla spoiny

y - odległość od skrajnych włókien

Nakładki należy dać na pólkach ponieważ I jest większe mimo Momentu gnącego mniejszego.

24. Obliczanie wytrzymałościowe spoiny pachwinowej łączącej pręt niesymetryczny (kątownik) z blachą węzłową

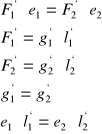
25. Obliczanie wytrzymałościowe spoiny pachwinowej obciążonej momentem skręcającym i siłą tnącą

między

= 0

26. Obliczanie wytrzymałościowe spoiny pachwinowej obciążonej momentem zginającym, siłą normalną i siłą tnącą na przykładzie dwuteownika przyspawanego czołowo do płyty.

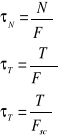
27. Połączenia gwintowe- rodzaje gwintów i ich zastosowanie, oznaczanie gwintów, rodzaje śrub, nakrętek i podkładek. Zabezpieczanie nakrętek przed odkręcaniem się.

Połączenia gwintowe wykonuje się za pomocą łączników gwintowych. Śruby, wkręty, nakrętki

Śruba to łącznik mający łeb ukształtowany tak aby można go było wkręcić odpowiednim kluczem. Trzpień śruby może być nagwintowany na całej swojej długości lub częściowo. Wykonane najczęściej przez toczenie z prętów walcowych lub ciągnionych czworokątnych. Śruby wykonywane z prętów okrągłych - łeb wykonuje się poprzez spęcznienie trzpienia i uformowanie łba.

Wkręty - łączniki mające łeb z wcięciem do wkrętaka

Nakrętki to elementy współpracujące ze śrubami lub wkrętami.

Rodzaje gwintów

a) trójkątne (stożkowe, walcowe)

zalety:

- zapewnia szczelność,

- przenosi duży moment skręcający,

- szybkie łączenie i rozkręcanie

Wady:

- trudne wykonanie,

- niemożność regulowania przesunięć osiowych

b) okrągły

- duża sztywność zmęczeniowa,

- nie jest stosowany w szerokim zakresie

c) gwinty dociskowe i napędowe - stosowane są trapezowe i prostokątne

Oznaczanie gwintów:

2^″; 3/4^″ - calowe

Tw 48 x 8 - trapezowy symetryczny

S 48 x 8 - trapezowy niesymetryczny

Rd 40 x 1/6^″ -okrągły

M30 -metryczny zwykły

M80 x 3 - metryczny drobnozwojowy

R 3/4^″Pt - rurowy przytępiony

Em 16 - Edisona metryczny

Rodzaje śrub:- śruba surowa- śruba półsurowa- śruba toczona- śruba dwustronna- śruba do drewna

Rodzaje nakrętek:- sześciokątne- czworokątne- dwuścienne- rowkowe- otworowe- skrzydełkowe- z uchem- radełkowe- koronowa

Rodzaje podkładek:

- sprężyste

Zabezpieczenie połączenia przed poluzowaniem lub odkręceniem pod wpływem przypadkowych sił np.:przy drganiach - specjalna podkładka, zapunktowanie trzpienia, zaklepanie trzpienia

Podkładka sprężysta z ostrymi odgiętymi końcówkami wciska się jednym końcem w nakrętkę a drugim w łączony element. Nakręcenie przeciwnakrętki, Nakrętka koronowa - przez otwór wycięty w śrubie przetyka się zawleczkę i rozgina końce, podkładki odginane, zębate

28. Sposoby wykonywania gwintów, materiały do produkcji śrub.

Poprzednie pytanie

Sposoby wykonywania gwintów:

- nacinanie

- frezowanie

- walcowanie- gwinty zewnętrzne trójkątne

- odlewanie gwintów ze stopów niezależnych

Materiały do produkcji śrub:

- stale automatowe - oznaczenie A10, A12 - zawartość węgla do 0,1%

29. Obliczanie sił potrzebnych do odkręcenia (wkręcenia) nakrętki obciążonej siłą osiową - szkice.

Obracając śrubę, możemy podnieść na pewna wysokość ciężar Q lub przezwyciężyć na pewnej drodze siłę Q.

Takie zastosowanie śruby do wykonania pewnej pracy jest szeroko spotykane w budowie maszyn, np.: podnośniki gwintowe.

Pracę wykonujemy przez działanie momentem M_s na śrubę. Zwój gwintu tworzy równię pochyłą o kącie nachylenia γ. Ciężar posuwany jest wzdłuż równi przez siłę H, leżącą w płaszczyźnie prostopadłej do osi śruby. Przedstawia ona działanie momentu M_s, którego wektor leży wzdłuż os śruby. Tarcie równi powoduje odchylenie reakcji od normalnej, do równi o kąt tarcia ρ. Rozkład sił działających na ciężar pokazany jest na rys. b,

N oznacza reakcję normalną równi, R zaś reakcję wypadkową z uwzględnienie siły tarcia, przy czym:

T = N⋅μ = N⋅tgρ μ - współczynnik tarcia

Z trójkątów sił obliczamy sile H, jaka jest potrzebna do poruszania ciężaru ruchem jednostajnym H = Q⋅tg(γ+ρ)

Gdybyśmy ciężar opuszczali, to zmieni się kierunek sił tarcia, a więc zmieni się ką, jaki tworzy ona z pionem

Ogólny zapis H = Q⋅tg(γρ)

przy czym znak „+” dotyczy ruchu ciężaru w górę, czyli podnoszenia, a znak „-” dotyczy opuszczania.

30. Sens fizyczny pozornego kąta tarcia. Moment potrzeby do okręcenia nakrętki.

Obliczenia dla gwintu o zarysie trapezowym lub trójkątnym.

W tym przypadku siła tarcia będzie większa niż przy gwincie prostokątnym. Do obliczenia siły tarcia trzeba bowiem w tym przypadku wziąć reakcję N', normalną do boku zarysu i tworzącą kąt α_r z siła N

Siła tarcia wynosi

T=N'⋅μ=

Jeżeli wyrażenie μ/cosα oznaczymy symbolem μ`, to możemy obliczyć sile tarcia ze wzoru:

T = N⋅ μ` = N⋅tgρ`

Wartość ρ` nazywamy pozornym kątem tarcia i obliczamy ze wzoru

tgρ` =

Moment potrzebny do okręcenia nakrętki:

M_s = 0,5⋅d_s⋅Q⋅tg(γ±ρ`)

31. Sprawność gwintu.

Sprawność gwintu jako maszyny roboczej wyrażamy stosunkiem pracy użytecznej do pracy włożonej. Sprawność dla przypadku zmiany pracy momentu obrotowego na pracę siły podłużnej

Praca użyteczna odniesiona do jednego obrotu śruby jest równa iloczynowi siły prze skok

L_u = Q⋅h = Q⋅π⋅d_s⋅tgγ

praca włożona w czasie jednego obrotu

L_w = 2⋅π⋅M_s = 0,5⋅2⋅π⋅Q⋅d_s⋅tg(γ+ρ`)

więc sprawność

η =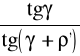

Sprawność śruby zależy od kąta pochylenia linii śrubowej i od współczynnika tarcia

32. Pojęcie samohamowalności gwintu. Wykres zależności sprawności gwintu od kąta wzniosu.

Śruba będzie samohamowalna, jeżeli dowolnie duża siła osiowa Q, obciążająca śrubę, nie wywoła jej obrotu. Warunek ten będzie spełniony, jeżeli przy opuszczaniu moment M_s będzie równy zero lub mniejszy od zera:

M_s = 0,5⋅d_s⋅Q⋅tg(γ+ρ`) ≤ 0

Nierówność ta będzie spełniona, jeżeli γ≤ ρ` - warunek samohamowalności śruby. Śruba jest samohamowalna, jeżeli kąt wzniosu linii śrubowej jest mniejszy od pozornego kąta tarcia. Śruby samohamowalne są mało sprawne.

Wykres zależności sprawności gwintu od kąta wzniosu,

Z wykresu widać, że przy wzroście kąta sprawności rośnie najpierw bardzo szybko, potem woniej. Stosujemy w śrubach różnie kąty γ. W mechanizmach, w których zależy nam na dużej sprawności, np. w prasach, stosujemy kąt γ = 18 ÷ 25^o.

W mechanizmach, które muszą być samohamowalne, np. podnośniki stosujemy kąt

γ = 4 ÷ 6^o.

W śrubach złączonych wymagana jest samohamowność, toteż stosujemy małe kąty

γ = 1,5 ÷ 5^o.

---