Równanie różniczkowe zupełne

Równanie różniczkowe zupełne to równanie postaci:

gdzie lewa strona równania jest różniczką zupełną pewnej funkcji

Całka ogólna równania ma postać
gdzie funkcję F wyznaczono z układu:

Warunkiem koniecznym i dostatecznym istnienia funkcji F jest równość odpowiednich pochodnych cząstkowych:

Przykład 1. Rozwiązać równanie:

Mamy kolejno:

a więc odpowiednie pochodne cząstkowe są równe.

Istnieje więc taka funkcja F, że

Wobec tego, przyjmując, że y jest stałe, dostajemy

więc w konsekwencji

Porównując odpowiednie pochodne cząstko­we stwierdzamy, że

czyli

a więc ostatecznie całka ogólna naszego równania ma postać:

• Równania różniczkowe rzędu drugiego

• sprowadzone do równań różniczkowych rzędu pierwszego

I. Równanie
.

Podstawiamy
.

Wtedy

i otrzymujemy równanie rzędu pierwszego
.

II. Równanie
.

Podstawiamy
.

Wtedy

i
.

III. Równanie
, gdzie F - jednorodne względem zmiennych
tzn.

dla
.

Podstawiamy
, gdzie
.

Wtedy

.

przykłady

• Metoda uzmienniania stałej na przykładzie

Najpierw rozwiązujemy jednorodne:

y''(x) − y(x) = 0

Konstruujemy wielomian charakterystyczny

λ2 − 1 = 0

Stąd mamy rozwiązanie w postaci:

y = c1ex + c2e − x

Teraz uzmienniamy stałą

y = c1(x)ex + c2(x)e − x

Następnie tworzymy układ :

Rozwiązujemy układ w celu wyznaczenia c1 i c2

Metoda przewidywania. Metoda przewidywania może być stosowana, jeśli współczynnik równania
jest stały, a prawa strona równania
jest jedną z funkcji wymienionych w poniższej tabeli. Przewidujemy wówczas, że RSRN jest pewną funkcją
tego samego typu, co prawa strona
. Liczby
, występujące w
są niewiadome. Liczby
, występujące w przewidywanej funkcji
są niewiadome. Są tak zwane współczynniki nieoznaczone. W poniższych przykładach pokażemy jak oblicz się te współczynniki.

Dane jest równanie
. Wyznaczyć metodą przewidywania RSRN, a następnie RORN.

Współczynnik
równania jest stały i równy 5. Prawa strona równania jest typu
. A więc zgodnie z tabelą przewidujemy, że RSRN jest w postaci

Otrzymane wyrażenia podstawiamy do danego równania:

Porównując współczynniki po lewej i prawej stronie ostatniej równości, otrzymujemy:

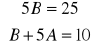
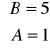
Podstawiając otrzymujemy:

RSRN:

Odpowiednie równanie jednorodne ma postać :

A więc RORN=RSRN+RORJ:
.

W dalszych przykładach ograniczymy się do obliczenia RSRN.